Avancement

Supposons qu’une transformation chimique est modélisée par la réaction suivante :

Et supposons que les quantités initiales soient :

Que deviennent ces quantités
si la réaction a lieu une fois ?

Si elle a lieu une deuxième fois ?

Et une troisième fois ?

La réaction peut-elle continuer ?

Non

C'est un réactif limitant

Que se serait-il passé avec les quantités suivantes ?

Que dit-on alors du mélange ?

Le mélange est
en proportion stœchiométrique.
Ou plus simplement :
le mélange est stœchiométrique.

Si la réaction est $\ce{a A + b B -> …}$,
quelle relation doit lier les quantités de matière initiales $n_{A}$ et $n_B$ pour que le mélange soit
en proportion stœchiométrique ?

$\displaystyle \frac{n_A}{a}=\frac{n_B}{b}$

Retournons à notre réaction

Mais imaginons maintenant que les quantités initiales soient beaucoup, beaucoup plus grandes. Il faut trouver un moyen plus pratique de tenir les comptes.

Désignons par $x$
le nombre de fois que la réaction a lieu.
On appelle $x$ l'avancement de réaction.

Comment évolue les quantités de matière
des réactifs et des produits en fonction de $x$ ?

Comment se représenter
cette évolution graphiquement ?

Pour faire les comptes, on classe ces infos
dans un tableau : le tableau d’avancement.

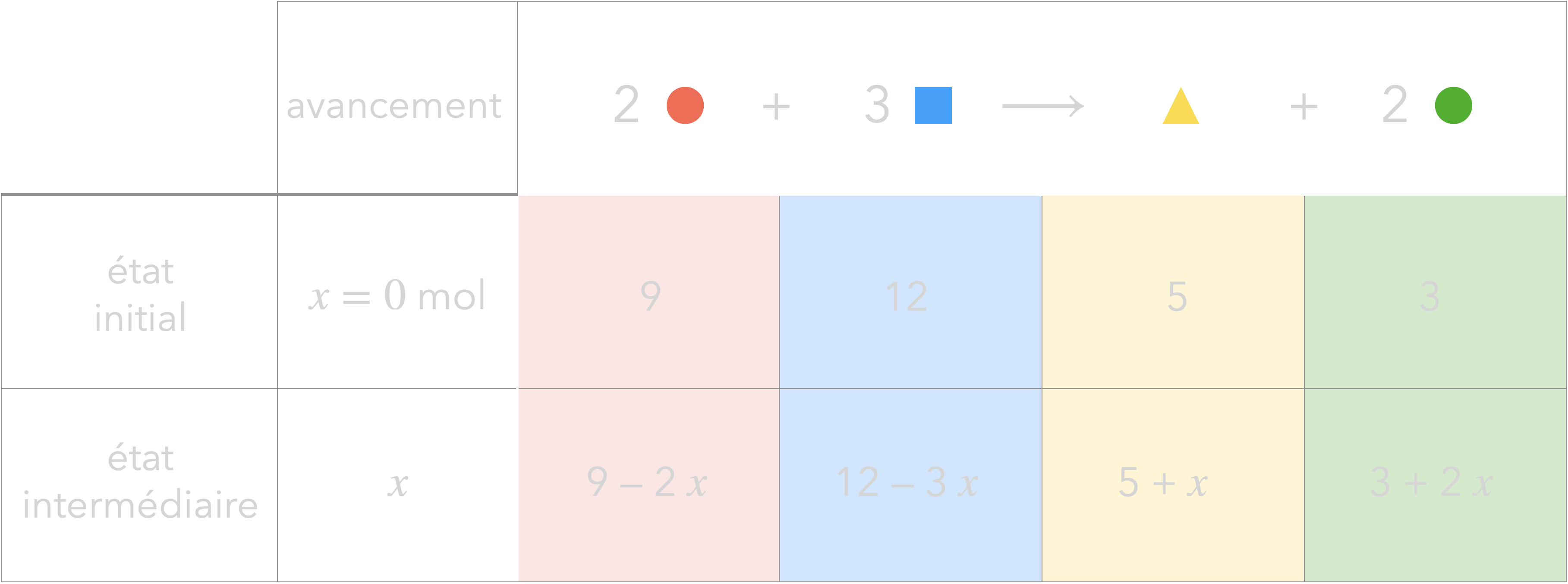
Détermination
de la composition finale

L’avancement en fin de réaction
est appelé avancement final $x_f$.

L’avancement maximal $x_{max}$ est lui l’avancement correspondant à la disparition totale d’un réactif.
Ce réactif est le réactif limitant.

Comme la disparition totale d’un réactif
n’est pas systématique, on a :

S’il y a effectivement disparition totale d’un réactif alors la transformation est dite totale. Et on a :

Si la transformation est totale, alors on peut déterminer $x_{max}$ en supposant tour à tour chacun
des réactifs comme limitant et en en déduisant l’avancement maximal $x_{max}$ correspondant.

L’avancement maximal réel est alors
le plus petit des $x_{max}$ trouvés.

Exemple :

• Si
  est limitant, alors on a :
  $$9-2\, x_{max\color{#FF644E}\Large\bullet} = 0$$
  $$ \begin{aligned} \Rightarrow x_{max\color{#FF644E}\Large\bullet} &= \frac{\pu{9 mol}}{2}\\ &= \pu{4,5 mol} \end{aligned} $$

• Si
  est limitant, alors on a :
  $$12-3\, x_{max\color{#00A2FF}\small\blacksquare} = 0$$
  $$ \begin{aligned} \Rightarrow x_{max\color{#00A2FF}\small\blacksquare} &= \frac{\pu{12 mol}}{3}\\ &= \pu{4 mol} \end{aligned} $$

$ \begin{aligned} x_{max} &= \min(x_{max\color{#FF644E}\Large\bullet},x_{max\color{#00A2FF}\small\blacksquare})\\ &= \pu{4 mol} \end{aligned} $

L’état final peut maintenant être ajouté
au tableau d’avancement :

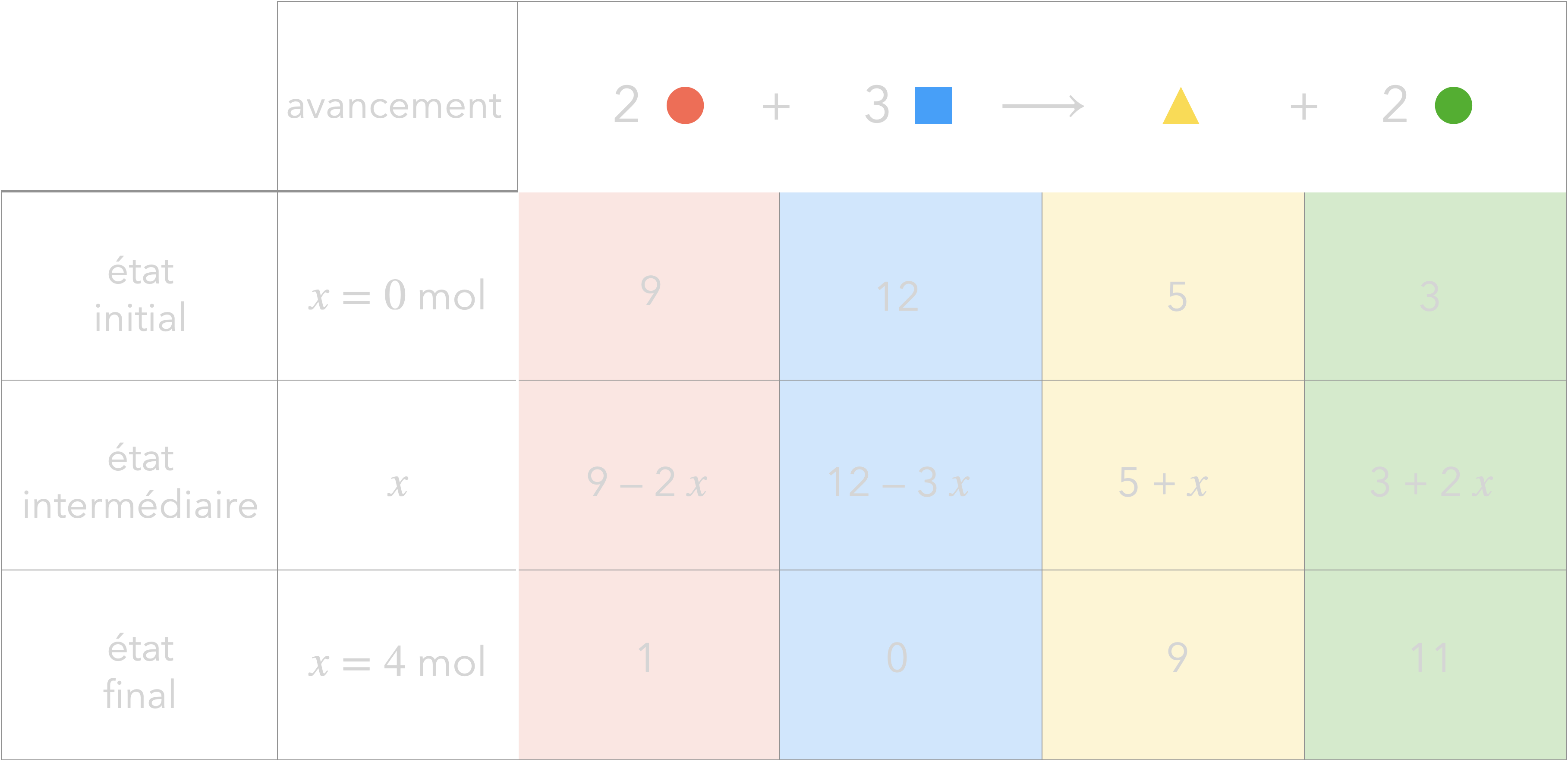
On retrouve bien ce qu’on pouvait déduire
de la représentation graphique.

Autre exemple

Transformation entre le diiode et les ions thiosulfate

Réaction modélisant la transformation étudiée :

Quantités initiales :

• $n_{\ce{I2}\text{,initial}} = n_1 = \pu{4,0E-3 mol} = \pu{4,0 mmol}$
• $n_{\ce{S2O3^2-}\text{,initial}} = n_2 = \pu{5,0E-3 mol} = \pu{5,0 mmol}$
• $n_{\ce{I-}\text{,initial}} = n_3 = \pu{0 mol}$
• $n_{\ce{S4O6^2-}\text{,initial}} = n_4 = \pu{0 mol}$

Dresser un tableau d'avancement.

On supposera la transformation totale.

Déterminer le réactif limitant et l'avancement final.

• Si $\ce{I2}$ est limitant :
  $n_1- x_{max1} = 0$
  $$ \Rightarrow x_{max1} = n_1 = \pu{4,0 mmol}\\ $$
• Si $\ce{S2O3^2-}$ est limitant :
  $n_2-2\, x_{max2} = 0$
  $$ \begin{aligned} \Rightarrow x_{max2} &= \frac{n_2}{2}\\ &= \pu{2,5 mmol} \end{aligned} $$

Comme $x_{max2}<x_{max1}$, $\ce{S2O3^2-}$ est le réactif limitant

et $x_f = x_{max} = \pu{2,5 mmol}$.

Déterminer l'état final.

Deuxième situtation

Quantités initiales :

• $n_{\ce{I2}\text{,initial}} = n_1= \pu{2,0 mmol}$
• $n_{\ce{S2O3^2-}\text{,initial}} = n_2 = \pu{5,0 mmol}$
• $n_{\ce{I-}\text{,initial}} = n_3 = \pu{0 mol}$
• $n_{\ce{S4O6^2-}\text{,initial}} = n_4 = \pu{0 mol}$

Dresser un tableau d'avancement.

On supposera la transformation totale.

Déterminer le réactif limitant et l'avancement final.

• Si $\ce{I2}$ est limitant :
  $n_1- x_{max1} = 0$
  $$ \Rightarrow x_{max1} = n_1 = \pu{2,0 mmol}\\ $$
• Si $\ce{S2O3^2-}$ est limitant :
  $n_2-2\, x_{max2} = 0$
  $$ \begin{aligned} \Rightarrow x_{max2} &= \frac{n_2}{2}\\ &= \pu{2,5 mmol} \end{aligned} $$

Comme $x_{max1}<x_{max2}$, $\ce{I2}$ est le réactif limitant

et $x_f = x_{max} = \pu{2,0 mmol}$.

Déterminer l'état final.

Troisième situtation

Quantités initiales :

• $n_{\ce{I2}\text{,initial}} = n_1= \pu{2,5 mmol}$
• $n_{\ce{S2O3^2-}\text{,initial}} = n_2 = \pu{5,0 mmol}$
• $n_{\ce{I-}\text{,initial}} = n_3 = \pu{0 mol}$
• $n_{\ce{S4O6^2-}\text{,initial}} = n_4 = \pu{0 mol}$

Dresser un tableau d'avancement.

On supposera la transformation totale.

Déterminer le réactif limitant et l'avancement final.

• Si $\ce{I2}$ est limitant :
  $n_1- x_{max1} = 0$
  $$ \Rightarrow x_{max1} = n_1 = \pu{2,5 mmol}\\ $$
• Si $\ce{S2O3^2-}$ est limitant :
  $n_2-2\, x_{max2} = 0$
  $$ \begin{aligned} \Rightarrow x_{max2} &= \frac{n_2}{2}\\ &= \pu{2,5 mmol} \end{aligned} $$

Comme $x_{max1}=x_{max2}$,
les deux réactifs sont limitants en même temps.

Le mélange est stœchiométrique.

Et $x_f = x_{max} = \pu{2,5 mmol}$.

Déterminer l'état final.

Quatrième situation

Quantités initiales :

• $n_{\ce{I2}\text{,initial}} = n_1= \pu{2,5 mmol}$
• $n_{\ce{S2O3^2-}\text{,initial}} = n_2 = \pu{5,0 mmol}$
• $n_{\ce{I-}\text{,initial}} = n_3 = \pu{0 mol}$
• $n_{\ce{S4O6^2-}\text{,initial}} = n_4 = \pu{2,0 mol}$

Qu'est-ce qui change ?
Quel est le nouvel état final ?

Outil informatique

Tableau d’avancement de la réaction :

Petit programme Python réalisant la même chose :

Initialisation des variables

import matplotlib.pyplot as plt

# coefficients stœchiométrique
# aA A + aB B -> aC C + aD D
aA = 2
aB = 3
aC = 1
aD = 2
# quantités initiales
nA = 0.02
nB = 0.04
nC = 0.01
nD = 0
x = 0           # Initialisation de l'avancement
dx = 0.001      # Incrément d'avancement
X = [x]         # Liste stockant les valeurs successives d'avancement
NA = [nA]       # Liste stockant les quantités des matières du réactif A
NB = [nB]       # Idem pour le réactif B
NC = [nC]       # Idem pour le produit C
ND = [nD]       # Idem pour le produit D

cœur du programme :

while NA[-1] > 0 and NB[-1] > 0:
    x = x + dx
    X.append(x)
    NA.append(nA - aA * x)
    NB.append(nB - aB * x)
    NC.append(nC + aC * x)
    ND.append(nD + aD * x)

tracés

plt.figure(figsize=(15,10),dpi=150)
plt.plot(X, NA, 'r-', lw=1, label='nA')
plt.plot(X, NB, 'g-', lw=1, label='nB')
plt.plot(X, NC, 'b-', lw=1, label='nC')
plt.plot(X, ND, 'y-', lw=1, label='nD')
plt.grid(True)
plt.xlabel('x (mol)')
plt.ylabel('n (mol)')
plt.legend()
plt.show()

Question subsidiaire :

Établir le tableau d’avancement
auquel correspond ce graphe.