Correction avancement

Taux d’alcoolémie

Un seul réactif coloré et le seul produit coloré est d’une autre couleur. En réglant le spectrophotomètre sur la longueur d’onde d’absorbance maximale du réactif,
on va pouvoir suivre l’évolution de la concentration du réactif en solution ; plus sa concentration sera faible
(et donc plus l’avancement sera grand),
plus l’absorbance sera faible elle aussi.

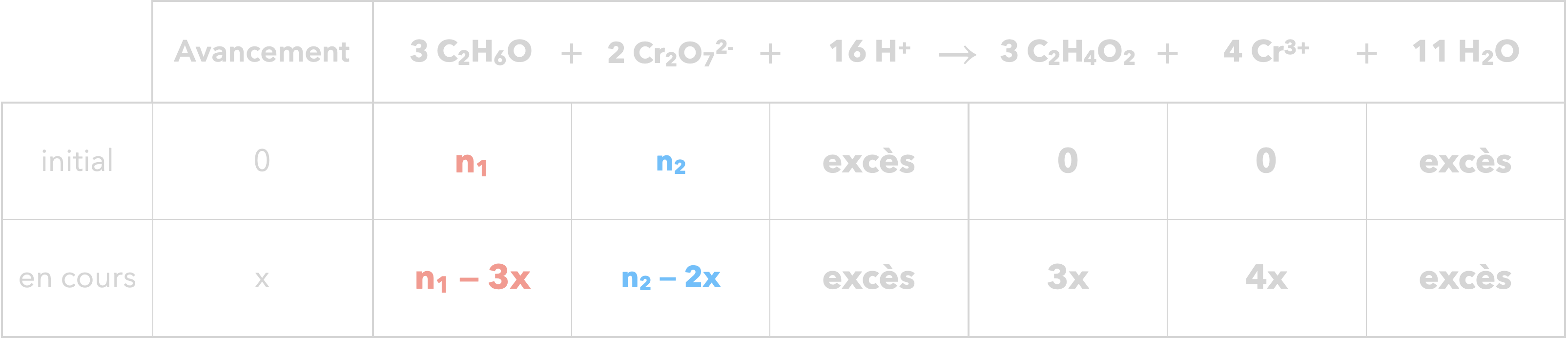
$ \begin{aligned} n_2 &= [\ce{Cr2O7^2-}]_0 \times V_2 \\ &= (\pu{2,0E-2 mol*L-1})\times (\pu{10,0 mL})\\ &= (\pu{2,0E-2 mol*L-1})\times (\pu{10,0E-3 L})\\ &= \pu{2,0E-4 mol} \end{aligned} $

$ n_2 - 2\, x_{max} = 0 $

$ \begin{aligned} \Rightarrow x_{max} &= \frac{n_2}{2} \\ &=\frac{\pu{2,0E-4 mol}}{2}\\ &= \pu{1,0E-4 mol} \end{aligned} $

$ \displaystyle [\ce{Cr2O7^2-}] = \frac{n_2 - 2x}{V} $

$ \begin{aligned} A_{420} &= k \times [\ce{Cr2O7^2-}]\\ & = k\times \frac{n_2 - 2x}{V} \end{aligned} $

$\displaystyle \Rightarrow \frac{V A_{420}}{k} = n_2 - 2x $

$\displaystyle \Rightarrow 2x=n_2 - \frac{VA_{420}}{k} $

$ \begin{aligned} \Rightarrow x&=\frac{n_2}{2} - \frac{VA_{420}}{2k}\\ & = 1,0\times \color{#56C1FF}10^{-4}\color{#93a1a1} - \frac{12\times \color{#88FA4E}10^{-3} \color{#93a1a1}A_{420}}{2\times 150}\\ & =1,0\times \color{#56C1FF}10 \times 10^{-5}\color{#93a1a1} - \frac{12\times \color{#88FA4E}100\times 10^{-5}\color{#93a1a1} A_{420}}{300}\\ &=10 \color{#FF968D}\times 10^{-5}\color{#93a1a1} - \frac{1200}{300}\times A_{420}\color{#FF968D}\times 10^{-5}\\ & = (10 - 4\times A_{420})\color{#FF968D}\times 10^{-5}\color{#93a1a1}\; \pu{mol} \end{aligned} $

$ \begin{aligned} x_f& = (10 - 4\times 2,39)\times 10^{-5}\\ & = \pu{4,4E-6 mol} \end{aligned} $

Comme la réaction est supposée totale, $x_f = x_{max}$.
Or cela nous donne un $x_{max}$ plus petit que celui qu’on a trouvé en supposant le dichromate limitant.
C’est donc l’éthanol qui est limitant !

$n_1 - 3\,x_{max} = 0$

$ \begin{aligned} \Rightarrow n_1& = 3\, x_{max}\\ & = 3\times\pu{4,4E-6 mol}\\ &=\pu{1,3E-5 mol} \end{aligned} $

Cherchons la masse d’éthanol dans les 2 mL :

$ \begin{aligned} m_2& = n_2\times M(\ce{C2H6O})\\ & = n_2\times (2M(\ce{C})+6M(\ce{H})+M(\ce{O}))\\ &=(\pu{1,3E-5 mol})\times (\pu{46 g*mol-1})\\ &=\pu{6,0E-4 g} \end{aligned} $

On en aura $\frac{\pu{1000 mL}}{\pu{2 mL}}=500$ fois plus dans un litre.

Cela donne :

$ \begin{aligned} m& =500\times \pu{6,0E-4 g}\\ & = \pu{0,30 g} \end{aligned} $

$\pu{0,30 g} < \pu{0,5 g}$ donc le conducteur
n’est pas en infraction.

chameaux

$\ce{2 C57H110O6 + 163 O2 -> 114 CO2 + 110 H2O}$

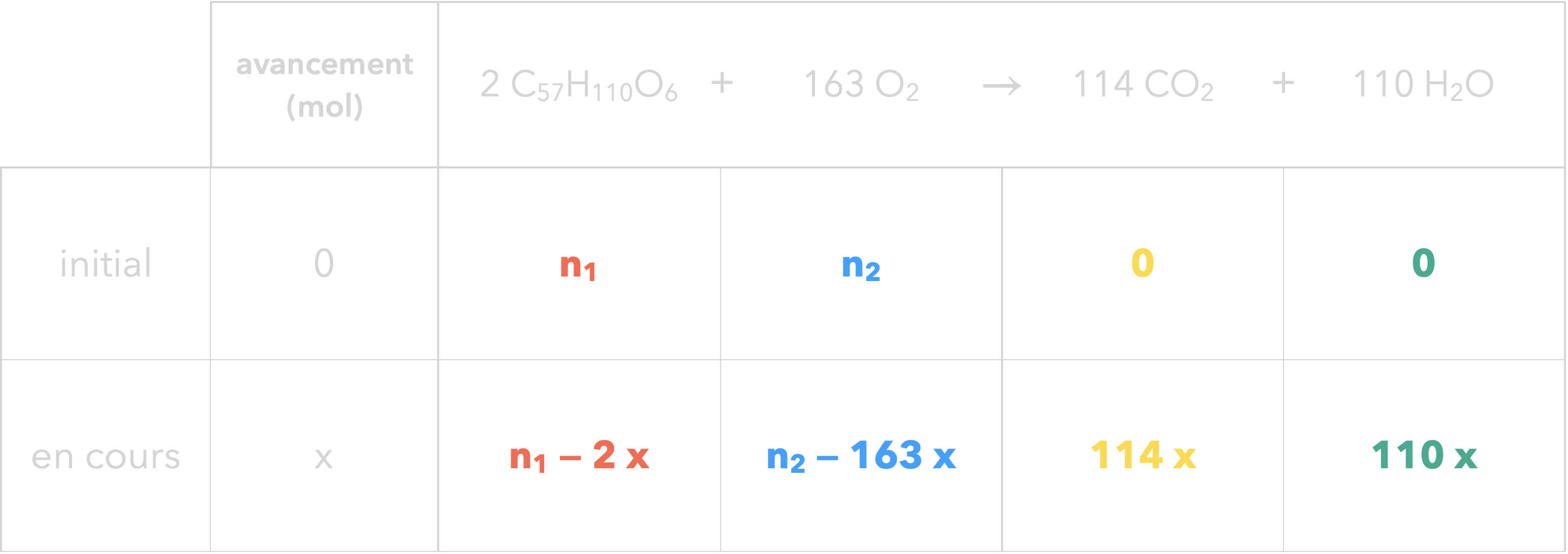
Cherchons $n_1$ :

$ \begin{aligned} M(\ce{C57H110O6}) &= 57\,M(\ce{C}) + 110\,M(\ce{H}) + 6\,M(\ce{O}) \\ &= \pu{890 g*mol-1} \end{aligned} $

$ \begin{aligned} n_1 &= \frac{m}{M}\\ &= \frac{\pu{1,0 kg}}{\pu{890 g*mol-1}}\\ &= \frac{\pu{1,0E3 g}}{\pu{890 g*mol-1}}\\ &= \pu{1,1 mol} \end{aligned} $

On suppose la transformation totale
et la tristéarine limitante :

$n_1 - 2\, x_{max} = 0$

$ \begin{aligned} \Rightarrow x_{max} &= \frac{n_1}{2}\\ & = \pu{5,5E-1 mol} \end{aligned} $

Pour déterminer la quantité de matière nécessaire
en dioxygène, on va supposer que le mélange
est stœchiométrique et donc que
le dioxygène est lui aussi limitant.

On obtiendra bien ainsi la quantité de matière minimale en dioxygène.

$n_2 - 163\, x_{max} = 0$

$ \begin{aligned} \Rightarrow n_2 &= 163\,x_{max}\\ & = \pu{90 mol} \end{aligned} $

Quantité de matière d’eau libérée :

$ \begin{aligned} n_\ce{H2O} &= 110\, x_{max} \\ &= \pu{61 mol} \end{aligned} $

Masse d’eau formée :

$ \begin{aligned} m_\ce{H2O} &= n_\ce{H2O}\times M(\ce{H2O}) \\ &= (\pu{61 mol})\times (\pu{18 g*mol-1})\\ & = \pu{1,1E3 g}\\ & = \pu{1,1 kg} \end{aligned} $

Volume d’eau formé (en L) :

$ \begin{aligned} V_\ce{H2O} &= \frac{m_\ce{H2O}}{\rho_\ce{H2O}} \\ &= \frac{\pu{1,1 kg}}{ \pu{1,0 kg*L-1}}\\ & = \pu{1,1L} \end{aligned} $

Le volume d’air nécessaire est 5 fois plus grand que le volume de dioxygène qu’on trouverait en supposant que l’air en est intégralement composé :

$ \begin{aligned} V_\text{air} &= 5 \times n_2 \times V_m \\ &= 5 \times \pu{90 mol} \times \pu{24 L*mol-1}\\\ & = \pu{1,1E4 L}\\ & = \pu{11 m^3} \end{aligned} $

eau oxygénée

10 volumes $\Rightarrow \pu{200 mL}\times 10 = \pu{2,0 L}$

$ \begin{aligned} n_\ce{O2} &= \frac{V}{V_m} \\ &= \frac{\pu{2,0 L}}{\pu{24 L*mol-1}}\\\ & = \pu{8,3E-2 mol}\\ \end{aligned} $

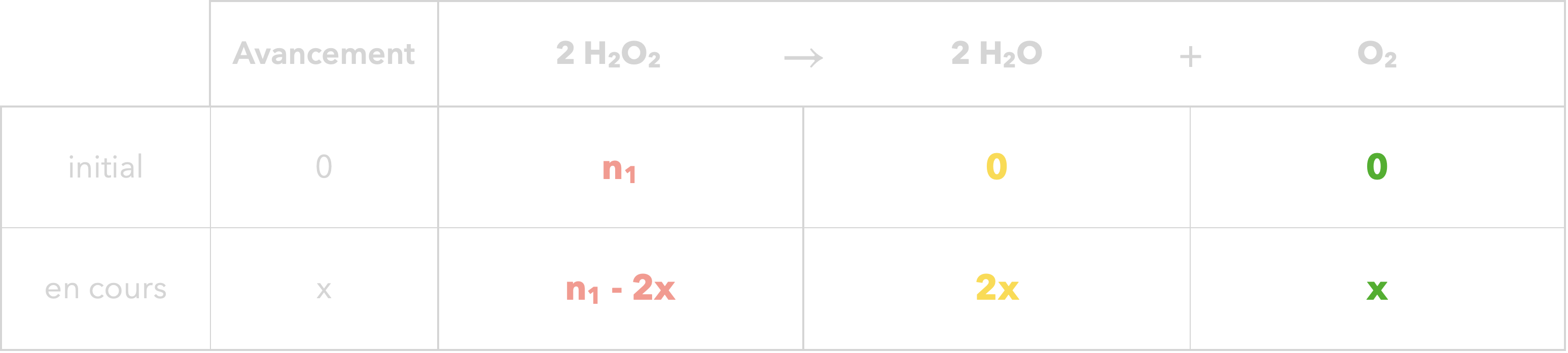
On connaît l’avancement final
puisqu’on a la quantité de $\ce{O_2}$ formé :

$x_f = n_\ce{O2} = \pu{8,3E-2 mol}$

En supposant la transformation totale, ça nous permet de déterminer la quantité initiale de peroxyde d’hydrogène (forcément limitant) :

$n_\ce{H2O2} - 2\, x_{max} = 0$

$ \begin{aligned} \Rightarrow n_\ce{H2O2} &= 2\,x_{max} \\ &= 2\times 8,3\times10^{-2}\\\ & = \pu{1,7E-1 mol}\\ \end{aligned} $

Cherchons la masse de peroxyde d’hydrogène :

$ \begin{aligned} m_\ce{H2O2} &= n_\ce{H2O2} \times M(\ce{H2O2})\\ &= (\pu{1,7E-1 mol}) \times (\pu{34 g*mol-1})\\\ & = \pu{5,8 g}\\ \end{aligned} $

On a donc 5,8 g pour 200 mL.

La masse des $V=\pu{200 mL}$
de solution est donnée par :

$ \begin{aligned} m_\text{solution} &= V\times \rho_\text{solution}\\ &= V\times d_\text{solution}\times \rho_\text{eau}\\ & = (\pu{200 mL})\times 1,0 \times (\pu{1,0 g*mL-1})\\ & = \pu{200 g} \end{aligned} $

Le pourcentage en masse vaut donc :

$ \begin{aligned} \frac{ m_\ce{H2O2}}{m_\text{solution}}\times 100 &= \frac{\pu{5,8 g}}{\pu{200 g}}\times 100\\ &= 2,9 \end{aligned} $

Pour une solution à 2,9 %,
il n’y a pas de protection à prendre.