Correction Bleu patenté
On cherche le nombre de verres de sirop pouvant être bus sans dépasser la DJA journalière.
Deux choses à déterminer :
-
À quelle quantité de matière la DJA journalière d’un adulte correspond-elle ?
-
Quelle quantité de matière en bleu patenté un verre de sirop contient-il ?
Le premier point est le plus facile :
La DJA du bleu patenté est de 2,5 mg
par kg de masse corporelle.
Prenons un adulte de 60 kg. Sa consommation journalière ne devra pas dépasser :
$$ \begin{aligned} m_{max} &= (\pu{60 kg})\times (\pu{2,5 mg/kg})\\ &= \pu{1,5E2 mg} \\ &= \pu{0,15 g} \end{aligned} $$
Cherchons la quantité de matière $n_{max}$ correspondante :
$$ \begin{aligned} n_{max} &= \frac{m_{max}}{M}\\ & = \frac{\pu{0,15 g}}{\pu{560,7 g*mol-1}}\\ & = \pu{2,7E-4 mol} \end{aligned} $$
Maintenant passons au 2e point :
la quantité de bleu patenté dans un verre.
Plusieurs étapes pour y arriver :
- Concentration :
- Détermination de la concentration de la solution S
- Détermination de la concentration du sirop
- Estimation du volume de sirop dans un verre
- Détermination de la quantité de matière en bleu patenté dans un verre de sirop
A.a. Détermination
de la concentration de la solution S
C’est le cœur de l’exercice !
Deux solutions pour l'obtenir :
- Par lecture graphique. La précision n'a pas besoin d'être extrême dans cet exercice puisqu'on est amené à faire des estimations.
- Par le calcul.
Solution calculatoire :
On commence déjà par dire que la courbe d'étalonnage obtenue confirme que la loi de Beer-Lambert est respectée sur la gamme étalon.
En effet, on voit sur le graphique que les points de mesure obtenus sont alignés avec l'origine.
L’absorbance $A$ des solutions étalons est donc proportionnelle à leur concentration $C$ : $A=k\times C$
De plus, l'absorbance de la solution S est dans la gamme (puisqu'elle est inférieure à 1,6). On peut donc lui appliquer la loi de Beer-Lambert !
Déterminons le coefficient de proportionnalité $k$ :
plutôt que de calculer la moyenne des coefficients pour chaque mesure, on peut constater que le point correspondant à S5 touche la droite.
Le rapport $A_5/C_5$ sera donc une bonne estimation du coefficient directeur de la droite (et d'autant meilleure que ce point est éloigné de l'origine).
On a donc :
$$ \begin{aligned} k&\approx\frac{A_5}{C_5}\\ &=\frac{\pu{0,16}}{\pu{1,0E-6 mol*L-1}}\\ &=\pu{1,6E5 L*mol-1} \end{aligned} $$
On peut maintenant déterminer la concentration $C$ de la solution S sachant que son absorbance mesurée vaut $A=0,75$ :
$$ \begin{aligned} A&=k\times C\\ \Rightarrow C&=\frac{A}{k}\\ &= \frac{\pu{}0,75}{\pu{1,6E5 L*mol-1}}\\ &= \pu{4,7E-6 mol*L-1} \end{aligned} $$
A.b. Détermination
de la concentration du sirop
La concentration en bleu patenté de la solution est donc de $\pu{4,7e-6 mol*L-1}$ et comme le sirop a été dilué 10 fois pour obtenir S, la concentration
du sirop est 10 fois plus grande :
Solution graphique :
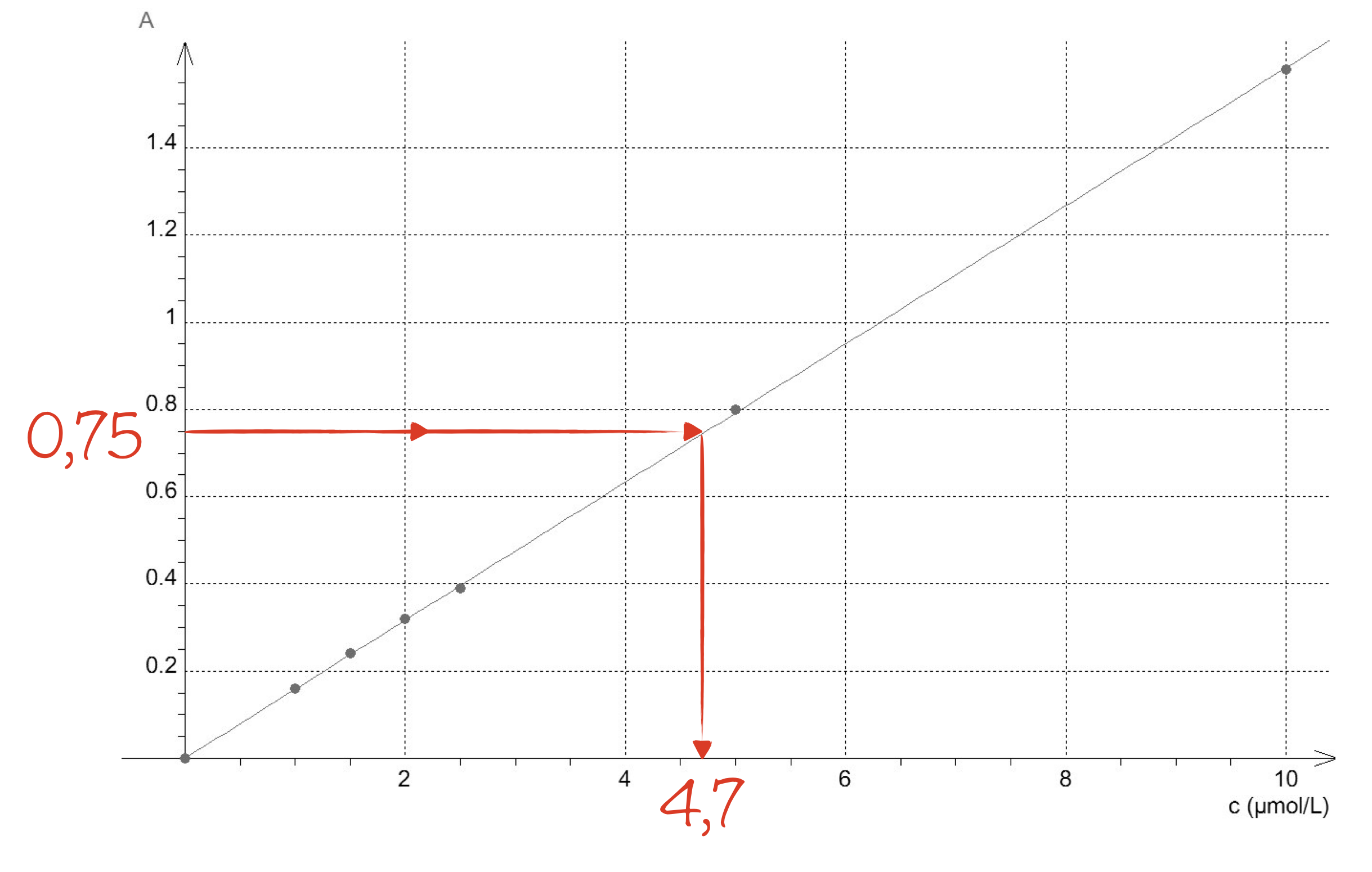
On obtient $4,7$ μ$\pu{mol*L-1}$ de bleu patenté dans la solution et donc $\pu{4,7e-5 mol*L-1}$ pour le sirop
La réponse est cohérente
par rapport aux calculs.
B. Passons au volume de sirop dans un verre :
Le volume typique d'un verre est de $\pu{20 cL}$
mais le sirop est généralement dilué.
Supposons que le sirop est dilué 10 fois
(il est généralement recommandé d'avoir
1 volume de sirop pour 9 volumes d'eau).
Cela fait alors un volume $V_{sirop}=\pu{2,0 cL}$.
Rq : on aurait aussi pu dire qu'un verre
contient au final la solution S...
C. On peut enfin déterminer la quantité de matière
en bleu patenté contenu dans un verre :
$$ \begin{aligned} n&=C_{sirop}\times V_{sirop}\\ &=\pu{4,7e-5 mol*L-1}\times \pu{2,0e-2 L}\\ &=\pu{9,4e-7 mol} \end{aligned} $$
Or on a vu au début que la quantité journalière à ne pas dépasser était $n_{max}=\pu{2,7e-4 mol}$.
Cela représente un nombre de verres :
$$ \left\lfloor\frac{n_{max}}{n}\right\rfloor = \left\lfloor\frac{\pu{2,7e-4 mol}}{\pu{9,4e-7 mol}}\right\rfloor = \pu{2,8E2} $$
Une personne de 60 kg ne doit donc pas boire plus de 280 verres de sirop par jour pour éviter la toxicité du bleu patenté.
Commentaire (à ne pas oublier car demandé explicitement et donc intervenant dans le barême) : il y a de la marge…