Énergie cinétique
L’énergie de mouvement d’un objet s’appelle :
l'énergie cinétique $E_c$
- $E_c$ en J
- $m$ en kg
- $v$ en $\pu{m*s-1}$
Exemples :
- une balle de tennis de 58,5 g partant de la raquette
à 200 km/h a une énergie cinétique de 90 J - un ballon de foot de 450 g partant du pied
à 100 km/h a une énergie cinétique de 174 J - une balle de 8,10 g sortant à 400 m/s du canon
d'un pistolet a une énergie cinétique de 650 J - un rugbyman de 100 kg courant à 25 km/h a une énergie cinétique de 2,4 kJ
Comment peut-on faire varier
l’énergie cinétique d’un système ?
Grâce au travail d'une force !
Travail d’une force
Pour modifier l’énergie cinétique d’un système,
il faut qu’au moins une force travaille.
Le travail d'une force $W$ est l'énergie
liée au déplacement d'une force.
Mais seule la composante du déplacement parallèle
à la force contribue au travail (en prenant
ou donnant de l’énergie au système).
On ne peut donc pas simplement multiplier la force par le déplacement, il faut faire un produit scalaire qui permet de multiplier la force par la projection du vecteur déplacement sur la direction de la force.
Pour une force $\vec{F}$ constante
sur un déplacement entre les points A et B :
- $W$ en J
- $F$ en N
- $AB$ en m
On voit ainsi que $\pu{1 J} = \pu{1 N*m} $
Le travail d’une force entre un point A
et un point B vaut donc le produit scalaire
entre cette force et le déplacement
$\overrightarrow{AB}$.
- Si $W>0$
$\Leftrightarrow \cos\alpha > 0$
$\Leftrightarrow$ force dans le sens du déplacement,
le travail est dit moteur - Si $W<0$
$\Leftrightarrow \cos\alpha < 0$
$\Leftrightarrow$ force dans le sens opposé au déplacement,
le travail est dit résistant
Cas particuliers :
La réaction normale au support (force du support sur le système en l’absence de frottement) est toujours perpendiculaire au déplacement.
Comme $\cos 90^\circ = $ $\;0$, son travail est donc nul.
On dit que la réaction normale ne travaille pas.
Le poids étant vertical, il ne travaille pas
si le déplacement est horizontal.
Et pour un déplacement entre
les points A et B d'altitudes $z_A$ et $z_B$ :
$$ W_{\!AB}(\vec{P}) = \overrightarrow{P}\cdot\overrightarrow{AB} = -mg(z_B-z_A) $$
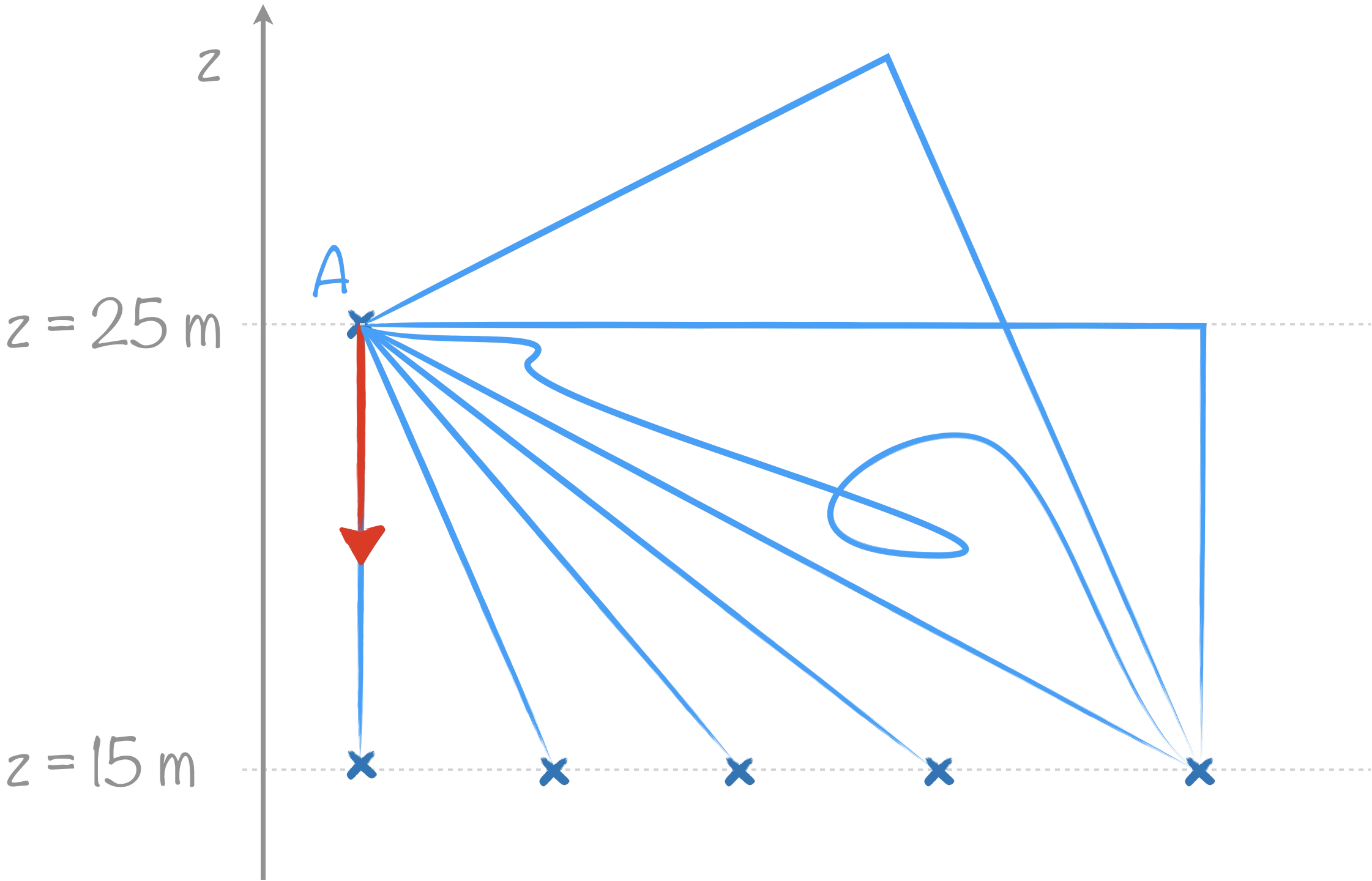
Que vaut le travail du poids pour un système de 100 g pour chacun des trajets suivant ?
Théorème de l’énergie cinétique
(TEC)
La variation d'énergie cinétique d'un système
entre un point A et un point B vaut la somme des travaux des forces extérieures sur le déplacement
$\overrightarrow{AB}$.
Conséquence :
si aucune force ne travaille sur un trajet $\overrightarrow{AB}$ (ou si
des travaux moteurs et résistants se compensent),
alors l’énergie cinétique est la même en B qu’en A
($\Rightarrow$ même vitesse).
Exercice :
Samson arrête une personne d’une masse m = 50 kg
lui arrivant dessus à une vitesse v = 10 m/s
en reculant d’une distance d = 1 m.

Que vaut la force F supposée constante
et horizontale qu’il doit appliquer ?
Un camion de 20 tonnes dévale une pente à 8%
à la vitesse de 72 km/h avant d’actionner ses freins.
Il met 500 m pour s’arrêter.
Que vaut la force de freinage (supposée constante) ?
On négligera les frottements autres
que ceux des freins et on prendra $g=\pu{10 m*s-2}$
Énergie cinétique initiale : $$ \begin{aligned} E_{cA} & = \frac{1}{2}mv^2_{A}\\ & = \frac{1}{2}\times 20\times 10^3 \times \left(\frac{72}{3,6}\right)^2\\ & = \pu{4E6 J} \end{aligned} $$
Énergie cinétique finale :
0 J (le camion s'arrête)
Bilan des forces :
- poids $\vec{P}$
- force de freinage $\vec{F}$
- réaction normale de la route $\vec{N}$
Calcul du travail de chacune de ces forces
sur le déplacement AB de 500 m :
- la réaction normale ne travaille pas puisqu'elle est perpendiculaire au déplacement : $W_{\!AB}(\vec{N}) = \pu{0 J}$
- le travail du poids dépend de la différence d'altitude entre le point de départ A et le point d'arrivée B : $W_{\!AB}(\vec{P}) = -mg(z_B-z_A)$
Ici, le dénivelé est de $\pu{500 m}\times 8\% = \pu{40 m}$, d'où $W_{\!\vec{P}} = -20\times 10^3\times 10 \times (-40) = \pu{8E6 J}$
Le travail du poids est positif $\Rightarrow$ il est moteur (normal, le poids aide à descendre).
- travail de la force de freinage : $W_{\!AB}(\vec{F}) = F\times AB\times \cos(180^\circ) = -500\times F$
le travail de la force de freinage est négatif
$\Rightarrow$ il est résistant (c'est son rôle !)
Plus qu'à appliquer le TEC pour relier
tout ce petit monde en une équation :
$$
E_{cB}-E_{cA} = W_{\!AB}(\vec{N}) + W_{\! AB}(\vec{P}) + W_{\!AB}(\vec{F})
$$
D'où $$ -\pu{4E6} = 0 + \pu{8E6} - 500\times F $$ $$ \Rightarrow F = \frac{\pu{-12E6}}{-500} = \pu{24 kN} $$
Énergie potentielle
Si le travail d’une force entre deux points A et B
ne dépend que des coordonnées de A et de B,
alors cette force est dite conservative.
Pouvez-vous citer un exemple de force conservative ?
Le poids est une force conservative.
En effet, on l'a vu, le travail du poids ne dépend
que de la différence d'altitude $z_B-z_A$
(pas du tout des points intermédiaires).
On peut associer à toute force conservative
une énergie potentielle telle que la variation
d’énergie potentielle entre deux points A et B
est opposée au travail de la force.
Dans le cas de la force conservative associée au champ de pesanteur terrestre (le poids), on obtient :
$\Delta E_{pp} = -W_{\!AB}(\vec{P}) = mg\left(z_B-z_A\right)$
En prenant pour origine de l’énergie potentielle
la même que celle des altitudes $z$
($E_{pp}(z=0)=0$)
on obtient la formule de
l’énergie potentielle de pesanteur
d’un système de masse $m$ à l’altitude $z$
(l’axe des $z$ est orienté vers le haut) :
Unités :
- $E_{pp}$ en $\pu{J}$
- $m$ en $\pu{kg}$
- $g$ en $\pu{N*kg-1}$
- $z$ en $\pu{m}$
Une force dont le travail dépend du chemin suivi (et pas seulement des extrémités) est dite non conservative.
C'est typiquement le cas des forces de frottements.
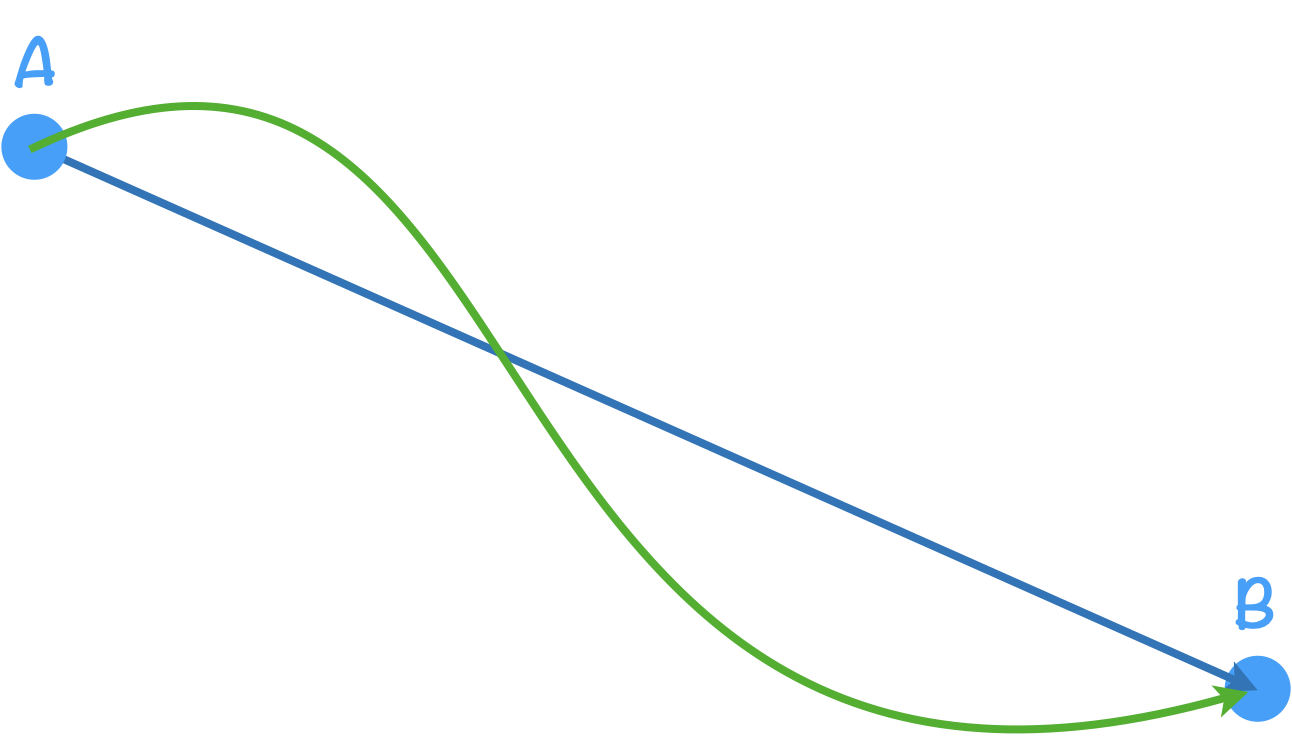
Le travail d’une force de frottement sera nécessairement plus grand sur le chemin vert alors que celui du poids sera le même sur les deux chemins.
Une force non conservative ne peut pas
être associée à une énergie potentielle.
Énergie mécanique
L’énergie mécanique d’un système est la somme de son énergie cinétique et de son énergie potentielle :
Si les forces agissant sur le système sont chacune
- soit conservatives
- soit de travail nul.
alors l’énergie mécanique du système se conserve.

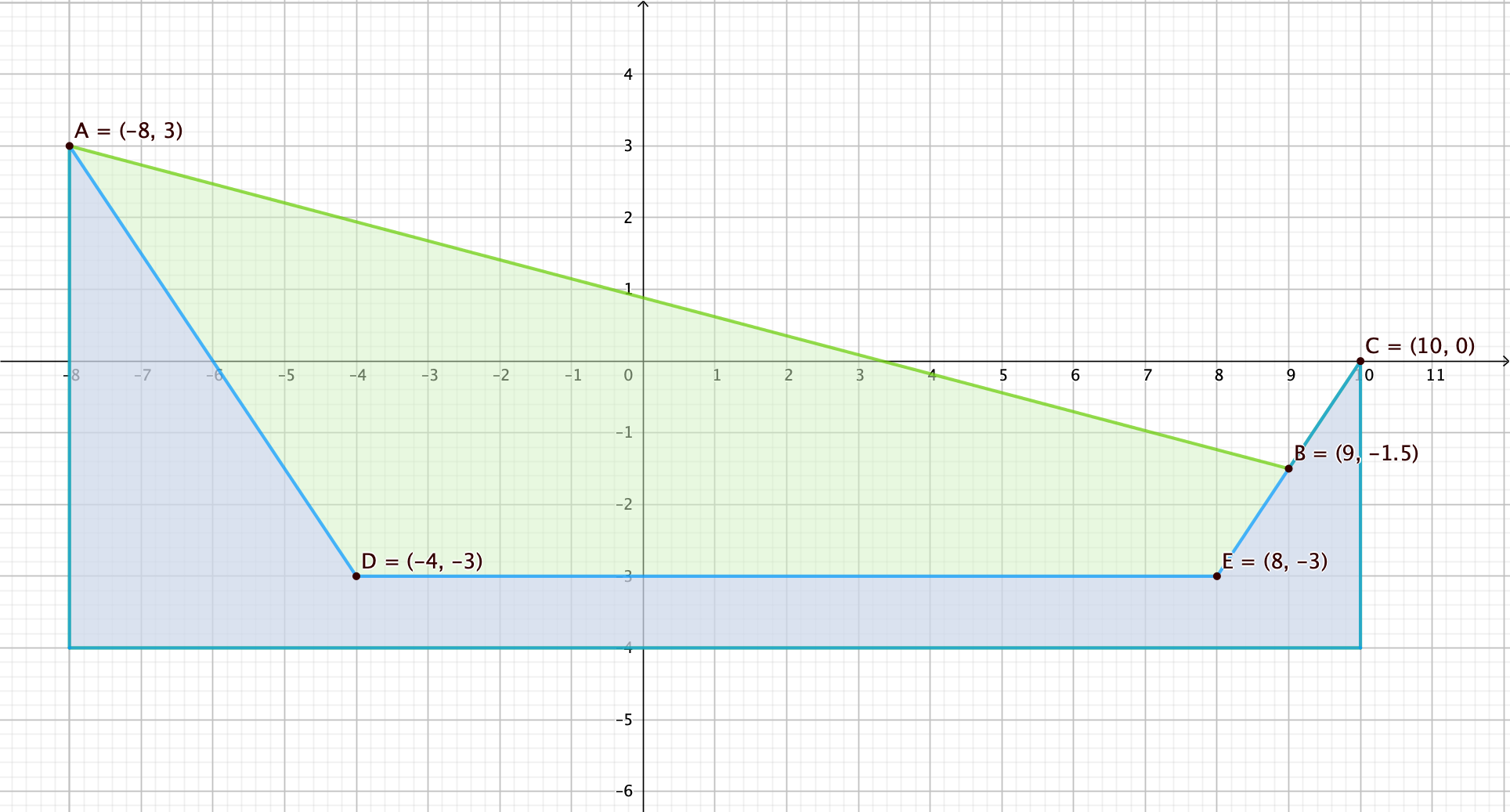
Quelle boule arrive en premier ?

Que vaut la vitesse en D ? En E ? En B ? Et en C ?
À l’inverse, si le système est soumis à des forces non conservatives qui travaillent, alors l’énergie mécanique du système n’est pas conservée.
Les forces non conservatives comme les frottements dissipent l’énergie mécanique.
Mais celle-ci n'a pas disparu ;
elle se retrouve convertie sous forme thermique.
Et la variation de l’énergie mécanique vaut donc
la somme des travaux des forces non conservatives
sur le chemin parcouru.
À quelle vitesse minimale doit sortir
l’eau du jet d’eau de Genève ?
Comment Armand “Mondo” Duplantis
va-t-il si haut ?

- masse : 79 kg
- taille : 1,81 m
Sachant qu’il va à $\pu{37 km*h-1}$
lorsqu’il plante sa perche,
à quelle hauteur peut-il
espérer monter ?
À quoi sert la perche au juste ?

Bonus : expliquer par un schéma pourquoi son centre de masse n’est pas obligé de passer
au-dessus de la barre.