Énergie électrique
Porteurs de charges
Un courant électrique est lié à un
mouvement de porteurs de charge électrique.
Dans un matériau conducteur, il s'agit d'électrons, chargés négativement ($q=-e=\pu{-1,6E-19 C}$).
Mais il peut aussi s'agir d'ions dans les solutions.
L’intensité $I$ d’un courant électrique continu mesure
le débit de charges (variation du nombre
de charges par unité de temps).
Unités :
- $I$ en ampères (A)
- $\Delta q$ en coulombs (C)
- $\Delta t$ en s
Combien d’électrons défilent à travers
la section d’un fil de cuivre pendant $\pu{1 s}$
si le courant qui y circule a une intensité de $\pu{1 A}$ ?
Pendant $\Delta t= \pu{1 s}$, il circule une charge $\Delta q=I\times \Delta t = \pu{1 C}$.
Comme les porteurs de charges dans un conducteur sont des électrons, le nombre d'électrons
qui circulent vaut :
$\displaystyle \frac{\Delta q}{e}=\frac{\pu{1 C}}{\pu{1,6E-19 C}} = \pu{6,3E18}$
Générateurs
Le courant continu dans un circuit est produit par
un générateur (ou source) de tension continue
(comme une pile).
À quoi devrait ressembler la caractéristique $U=f(I)$ d’un gérateur de tension continue ?
$E$ est la tension à vide du générateur ($U(I=0)$).
Dans un générateur de tension idéal, elle ne varie pas
(elle est indépendante de l’intensité).
Schéma du circuit électrique permettant de tracer expérimentalement la caractéristique d’un générateur réel de tension continue (une pile) ?
Réalisons l’expérience et traçons la caractéristique.
Quelle est l’équation de la courbe ?
$U=E-{\color{#FF968D}r}\times I$, avec $r>0$.
Dimension de $r$ ?
$[r]\times[I]=[U]$
$\displaystyle \Rightarrow [r]=\frac{[U]}{[I]}$
$r$ a la dimension d'une résistance.
Par quelle association de dipôles
pourrait-on modéliser le générateur réel ?
$r$ est la résistance interne du générateur.
générateur réel
=
générateur idéal
+
résistance (en série)
Conséquences de $r$ ?
- La tension fournie par le générateur est plus faible lorsque l'intensité fournie grandit.
- La résistance interne dissipe de l'énergie
(par effet joule). - Le générateur s'échauffe lorsque l'intensité augmente (toujours dû à la dissipation d'énergie).
Lien énergie-puissance
Qu’est-ce que l’énergie ?
L’énergie mesure la capacité à changer
la température ou
le mouvement d’un corps.
L’énergie est une sorte de monnaie d’échange qui passe d’une forme à une autre sans jamais disparaître (l’énergie se conserve !).
Et la puissance ?
La puissance mesure
le taux de variation de l'énergie
(sa vitesse de variation).
Formule liant les deux ?
Unités :
- $E$ en joules (J)
- $P$ en watts (W)
- $\Delta t$ en s
Donc $\pu{1 J} = \pu{1 W}\times \pu{1 s}$
En électricité, l’unité usuelle de l’énergie convertie est le killowatt-heure ($\text{kW}\!\cdot\!\text{h}$ souvent écrit $\pu{kWh}$).
Convertir $\pu{1 kWh}$ en $\pu{J}$. $$ \begin{aligned} \text{1 kWh} &= \text{1 kW} \times \text{1 h} \\ &= 10^3 \text{ W} \times 3600 \text{ s} \\ &= 3,6 \times 10^6 {\color{#FF968D}\text{ W}\cdot\text{s}} \\ &= 3,6 \times 10^6 {\color{#FF968D}\text{ J}} \end{aligned} $$
Et donc $\pu{1 kWh} = \pu{3,6 MJ}$.
Pourquoi les deux graphes diffèrent ?
Pouvez-vous en déduire le facteur de charge*
du nucléaire et celui de l'éolien ?
* rapport entre l'énergie électrique effectivement produite sur
une période donnée et l'énergie qui aurait été produite avec un fonctionnement à puissance nominale durant la même période.
Rendement d’un convertisseur
La quantité totale d’énergie se conserve
mais grâce à un convertisseur,
elle peut passer d’une forme à une autre.
Chaîne énergétique d’un convertisseur :
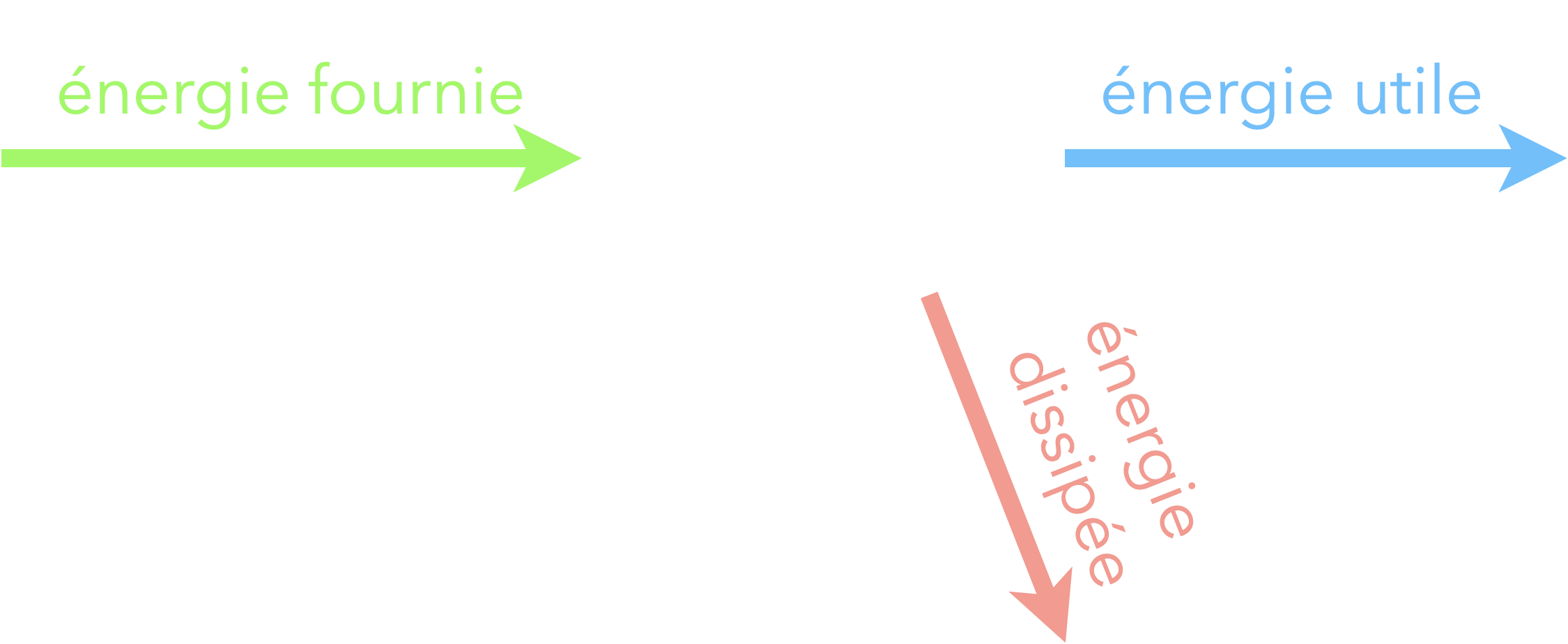
- L'énergie fournie peut être de différentes formes :
lumineuse, mécanique, électrique, thermique, chimique
- L'énergie utile résulte de la conversion de l'énergie fournie.
Suivant le convertisseur, elle peut aussi prendre différentes formes :
lumineuse, mécanique, électrique, thermique,chimique
- L'énergie dissipée correspond à l'énergie "perdue" dans la conversion (non convertie en énergie utile).
Elle est toujours sous forme thermique !
Par conservation de l’énergie :
énergie fournie = énergie utile + énergie dissipée
Le rendement $\eta$ d’un convertisseur est donné par :
Lorsque plusieurs conversions s’enchaînent,
les rendements se multiplient.
$\eta_\text{total} = \eta_\text{convertisseur 1}\times \eta_\text{convertisseur 2}\times\ldots$
Puissance électrique
Un dipôle électrique est soumis à une tension $U$ entre ses bornes et parcouru par un courant d’intensité $I$.
La puissance convertie par le dipôle s’écrit :
Unités :
- $P$ en watts (W)
- $U$ en volts (V)
- $I$ en ampères (A)
Ordres de grandeur :
| Appareil | Puissance |
|---|---|
| Veilleuse d’appareil | 1 W |
| Chargeur | 20 W |
| Lampe | 30 W |
| Ordinateur | 200 W |
| Téléviseur | 150 W |
| Appareil | Puissance |
|---|---|
| Fer à repasser | 1200 W |
| Lave-linge | 2500 W |
| Four | 3000 W |
| Plaque de cuisson | 6000 W |
Qu’ont en commun les appareils du 2e tableau ?
Effet joule
Les dipôles électriques dissipent de la puissance thermique du fait de leur résistance.
C'est l'effet Joule.
Un dipôle ohmique est justement caractérisé par sa résistance $R$. Il convertit l’intégralité de la puissance électrique reçue en puissance thermique.
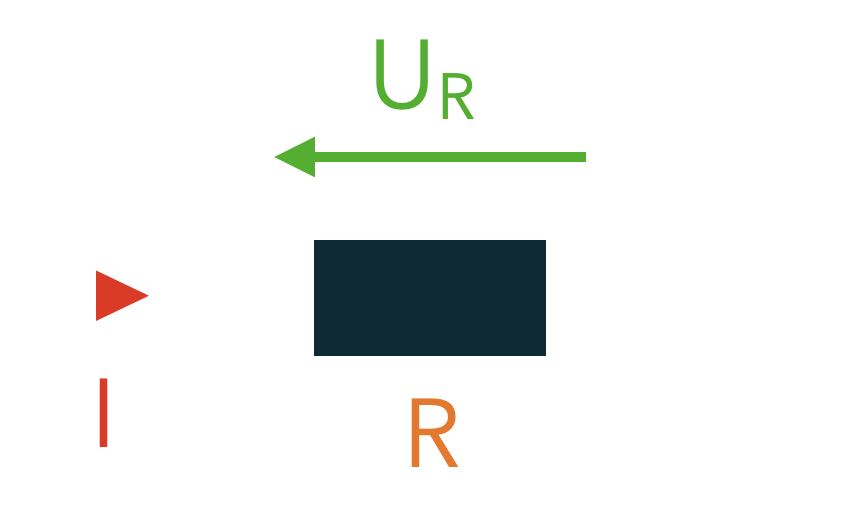
La puissance dissipée par effet Joule est donnée par :
On passe d'une formule à l'autre
en appliquant la loi d'Ohm.
Et l’énergie dissipée par effet Joule vaut donc :
Bilan de puissance dans un circuit
La puissance électrique fournie par un générateur vaut la somme des puissances électriques consommées
par chaque dipôle récepteur du circuit.
Exemple :
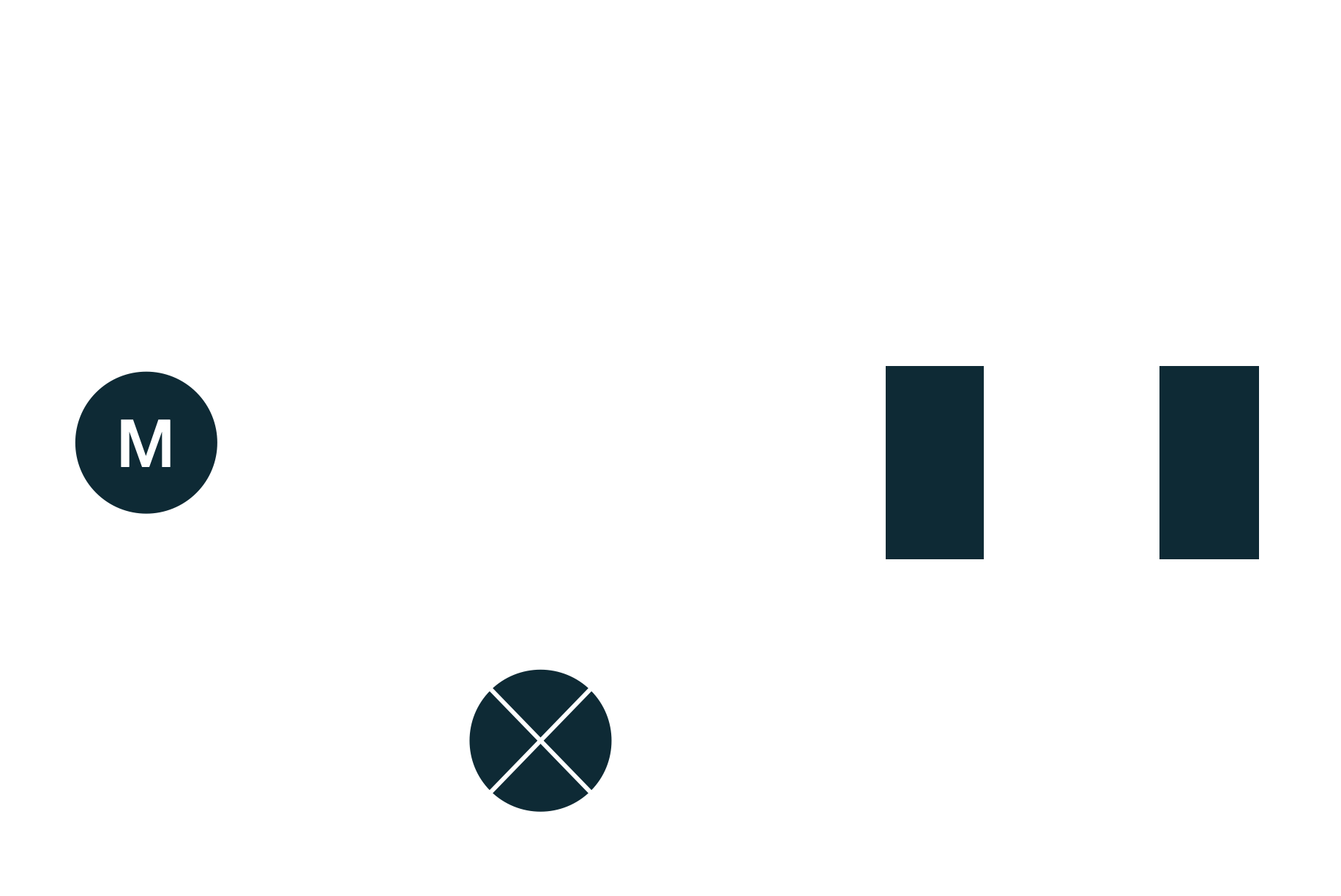
$P_G = P_M +P_L + P_{R_1} + P_{R_2}$