Fromation d’images par une lentille convergente

Mesures algébriques

Les mesures algébriques sont des longueurs
auxquelles on ajoute un signe.

On note $\overline{AB}$ la mesure algébrique entre $A$ et $B$.

Un axe horizontal (l’axe optique, généralement vers la droite) et un axe verical (généralement vers le haut) permettent de définir le sens positif.

Relation de conjugaison

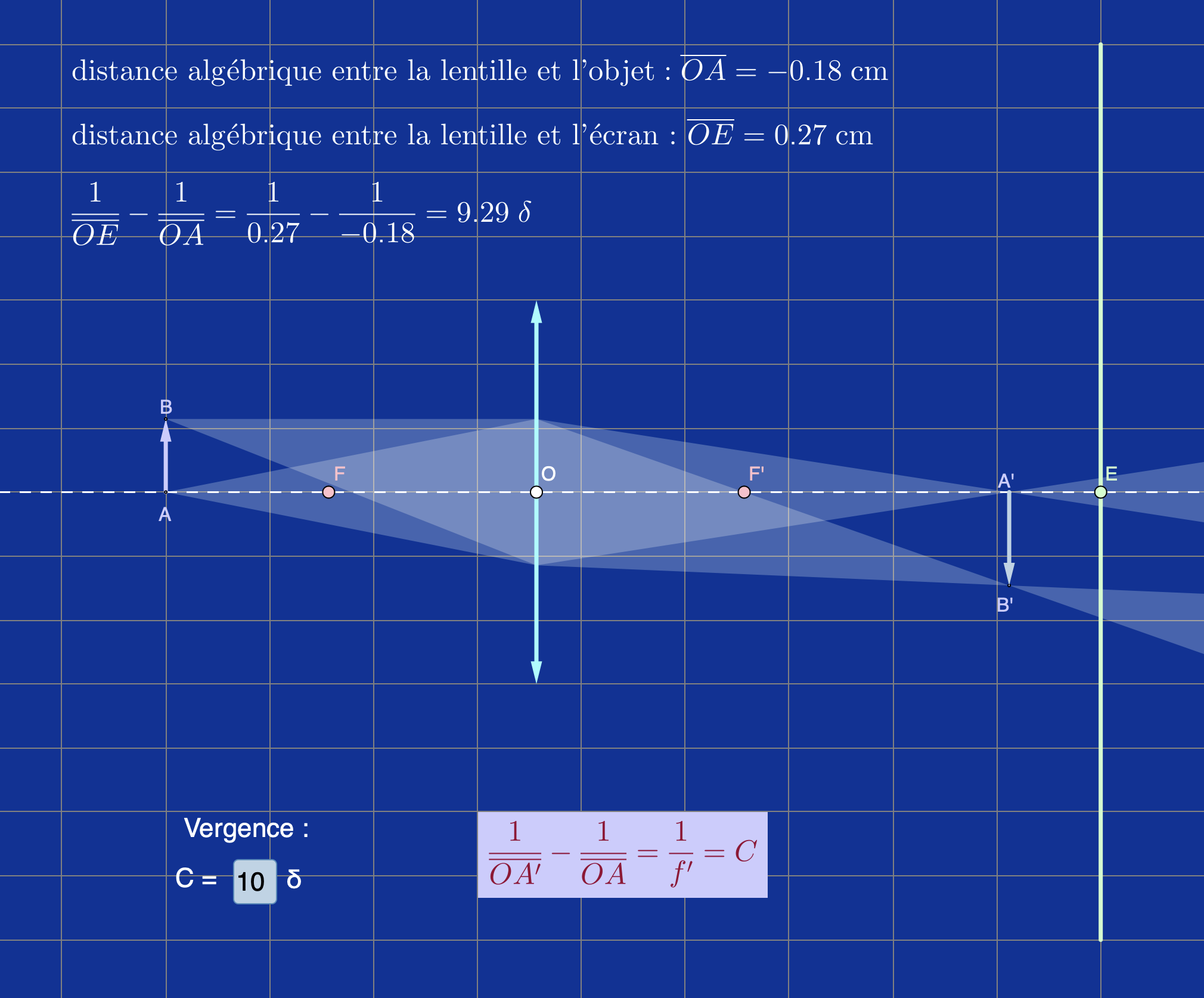
Dans la simulation précédente, la distance entre l’objet et l’écran est fixée et la position
de la lentille est modifiable.

Que remarque-t-on lorsque la position de la lentille permet d’avoir l’image de l’objet sur l’écran ?

Relation de conjugaison d’une lentille mince
(ou relation de Descartes)

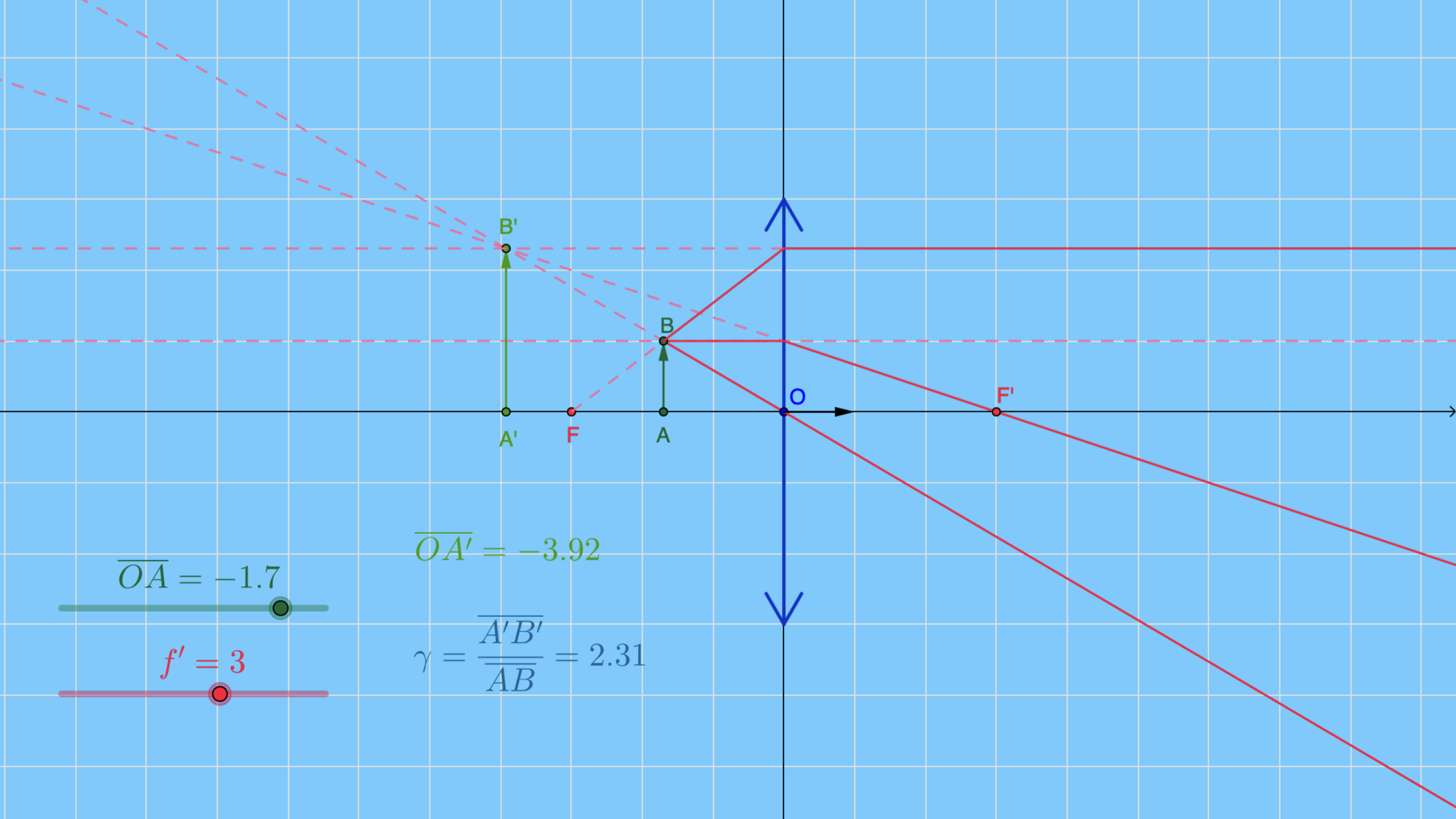
Définition de l’agrandissement algébrique $\gamma$ :

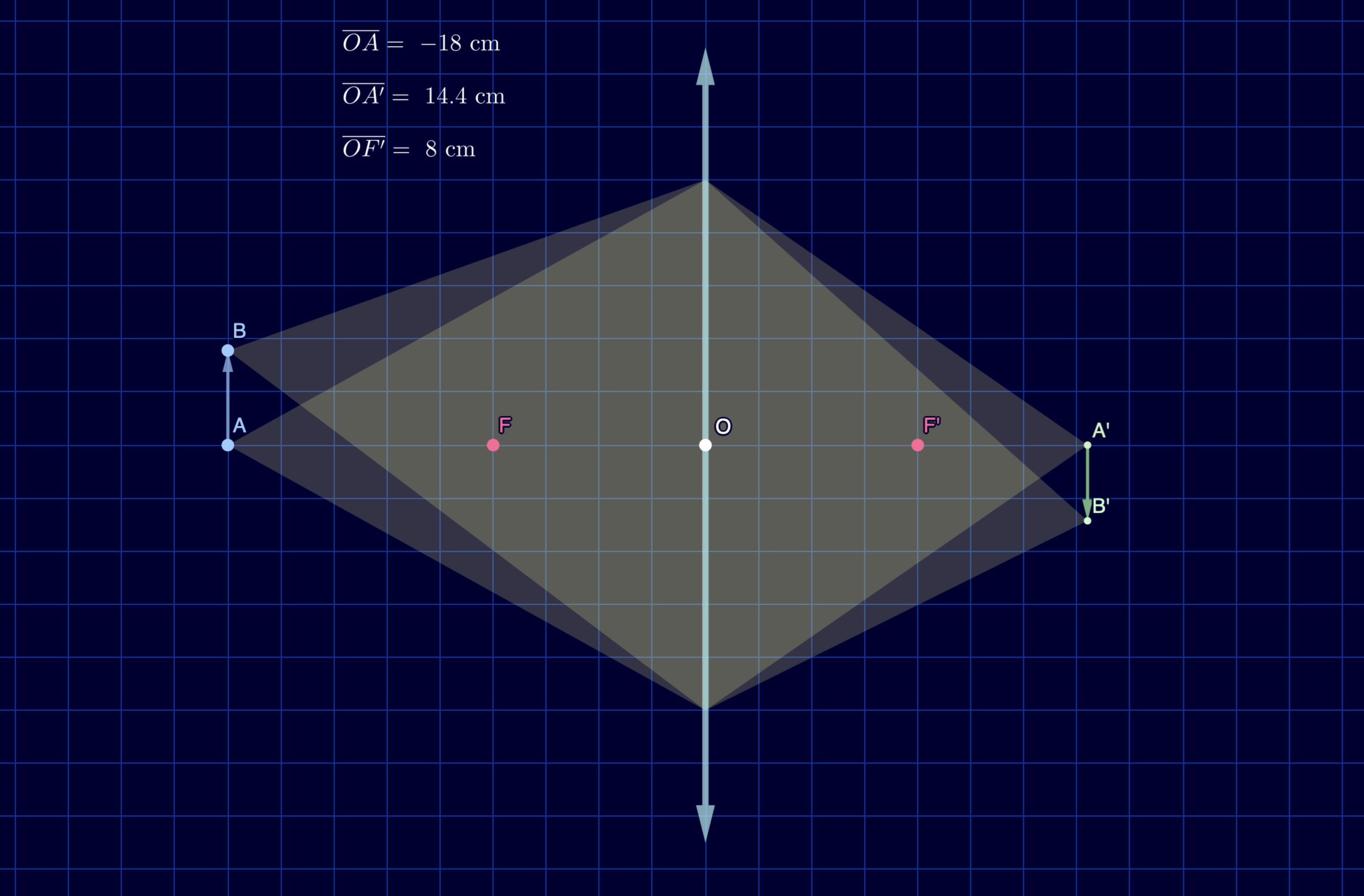
Le théorème de Thalès permet d’obtenir une formule ne dépendant plus des tailles de l’image et de l’objet mais de leur distance au centre optique de la lentille :

Caractéristiques de l’image d’un objet-plan réel formée par une lentille mince convergente

si
$-f' ≤ \overline{OA} ≤ 0$
(A entre F et O)

alors
$\overline{OA'} ≤ 0$ et $\gamma≥1$
L'image est virtuelle, droite et agrandie

si
$-f' ≤ \overline{OA} ≤ 0$
(A entre F et O)

alors
$\overline{OA'} ≤ 0$ et $\gamma≥1$
L'image est virtuelle, droite et agrandie

si
$-2f' ≤\overline{OA} ≤ - f'$

alors
$\overline{OA'} ≥ 2f'$ et $\gamma≤-1$
L'image est réelle, renversée et agrandie

si
$-2f' ≤ \overline{OA} ≤ - f'$

alors
$\overline{OA'} ≥ 2f'$ et $\gamma≤-1$
L'image est réelle, renversée et agrandie

si
$\overline{OA} ≤ - 2f'$

alors
$f' ≤ \overline{OA'} ≤ 2f'$ et $-1≤\gamma≤0$
L'image est réelle, renversée et réduite

si
$\overline{OA} ≤ - 2f'$

alors
$f' ≤ \overline{OA'} ≤ 2f'$ et $-1≤\gamma≤0$
L'image est réelle, renversée et réduite