Onde mécanique
Une onde mécanique progressive est une onde
qui se propage dans un milieu matériel.
Le milieu est composé de particules
capables d’osciller sur place.
Si l'une de ces particules est mise en mouvement
par une perturbation, elle va entraîner la mise en mouvement de ses voisines de proche en proche.
C'est ainsi que la perturbation
se propage dans le milieu.
On a alors propagation d’énergie et d’information
sans transport de matière.
C’est la définition d’une onde progressive.
Célérité et retard
Imaginons que la perturbation propagée par une onde atteigne le point A à l’instant $t_A$,
puis le point B à l’instant $t_B$.
On appelle retard la durée $\Delta t=t_B-t_A$.
Le retard $\Delta t$ et la distance $d=AB$ permettent de définir la célérité $c$ de l’onde :
- $d$ en $\pu{m}$
- $\Delta t$ en $\pu{s}$
- $c$ en $\pu{m*s-1}$
Périodicités spatiale et temporelle
Une onde est par essence
un phénomène spatiotemporel.
C’est-à-dire qu’elle se propage à la fois
à travers le temps et l’espace.
Une onde mécanique périodique est une onde
dont la perturbation se répète à l’identique.
Périodicité temporelle
à l'identique de la perturbation.
C'est la durée d'un motif.
La fréquence est l’inverse de la période :
- $f$ en $\pu{Hz}$
- $T$ en $\pu{s}$
Périodicité spatiale
à l'identique de la perturbation.
C'est la taille d'un motif.
- Dans un cas on visualise la variation de l'amplitude de la perturbation en un point de l'espace au cours
du temps $a(t)$ (c'est un enregistrement temporel).
La durée du motif est la période $T$. - Dans l'autre cas, on visualise à un instant donné
la variation de l'amplitude dans l'espace $a(x)$
(c'est une photo).
La taille du motif est la longueur d'onde $\lambda$.
Lien entre les deux périodicités ?
La célérité !
- $c$ en $\pu{m*s-1}$
- $\lambda$ en $\pu{m}$
- $T$ en $\pu{s}$
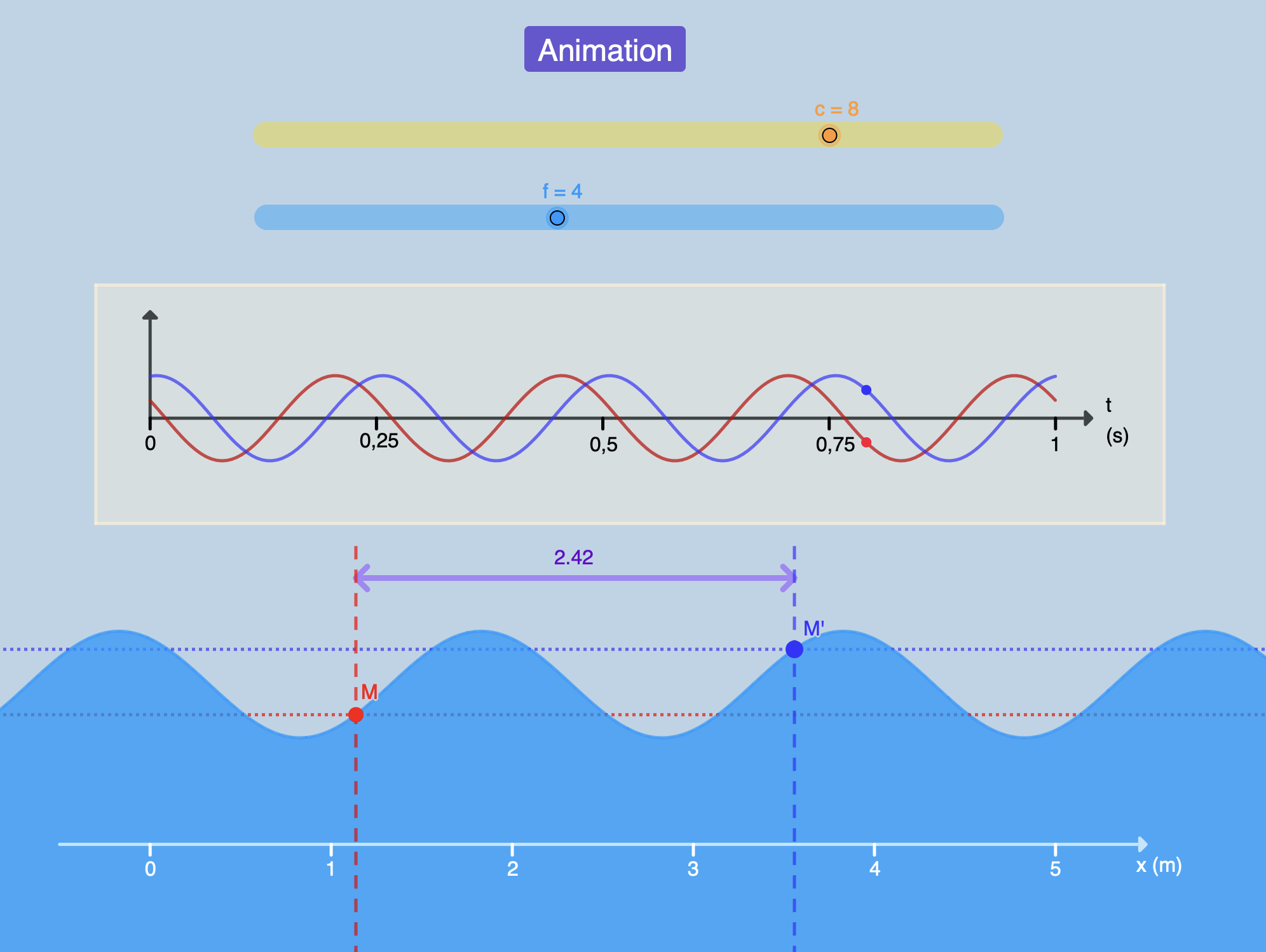
Les évolutions temporelles de deux points séparés par un nombre entier de longueurs d’onde sont identiques.
On dit alors que les signaux correspondant
à chacune des évolutions sont en phases.
Cela donne une méthode pour déterminer expérimentalement une longueur d'onde
(cf. 2e partie du TP).
Rq :
Sur l’animation, reculer un récepteur d’ultrasons par rapport à l’autre revient à reculer le point bleu par rapport au point rouge.
Une onde est dite sinusoïdale si la fonction modélisant l’évolution de la perturbation par rapport au temps
ou à la distance est elle-même sinusoïdale
(une fonction sinus ou cosinus).
Une onde sinusoïdale est a fortiori périodique
(la période est celle de la fonction sinusoïdale).
Mathématiquent : $\displaystyle a(t)=A\cos\left(2\pi\frac{t}{T}+\phi\right)$
ou
$\displaystyle a(x)=A\cos\left(2\pi\frac{x}{\lambda}+\psi\right)$