Le Son
Émission et perception
d’un son
Le son est produit par une vibration
qui se propage de proche en proche
dans un milieu matériel.
Les particules du milieu lui-même
ne font qu'osciller sur place.
On est en présence d’une onde (l’onde sonore) caractérisée par un transport d’énergie et d’information sans qu’il y ait transport de matière.
Sans milieu matériel, pas de son !
$\Rightarrow$ Le vide spatial est silencieux.
Par contre, plus le milieu matériel est dense
et plus le signal sonore se propage vite.
| milieu | air | eau | acier |
| vitesse du son (m/s) | 340 | 1500 | 5800 |
Comment convertir ces vitesses en km/h ?
Commençons par convertir des km/h en m/s
en prenant l’exemple de $\pu{72 km/h}$ :
$\pu{72 km/h}$ $\displaystyle =\frac{\pu{72 km}}{\pu{1 h}}$ $\displaystyle= \frac{\pu{72E3 m}}{\pu{3600 s}}$ $\displaystyle=\frac{\pu{72E3 m}}{\pu{3,6E3 s}}$
$$\Rightarrow \pu{72 km/h}=\frac{72}{\color{#E22146}{3,6}}\pu{ m/s}=\pu{20 m/s}$$
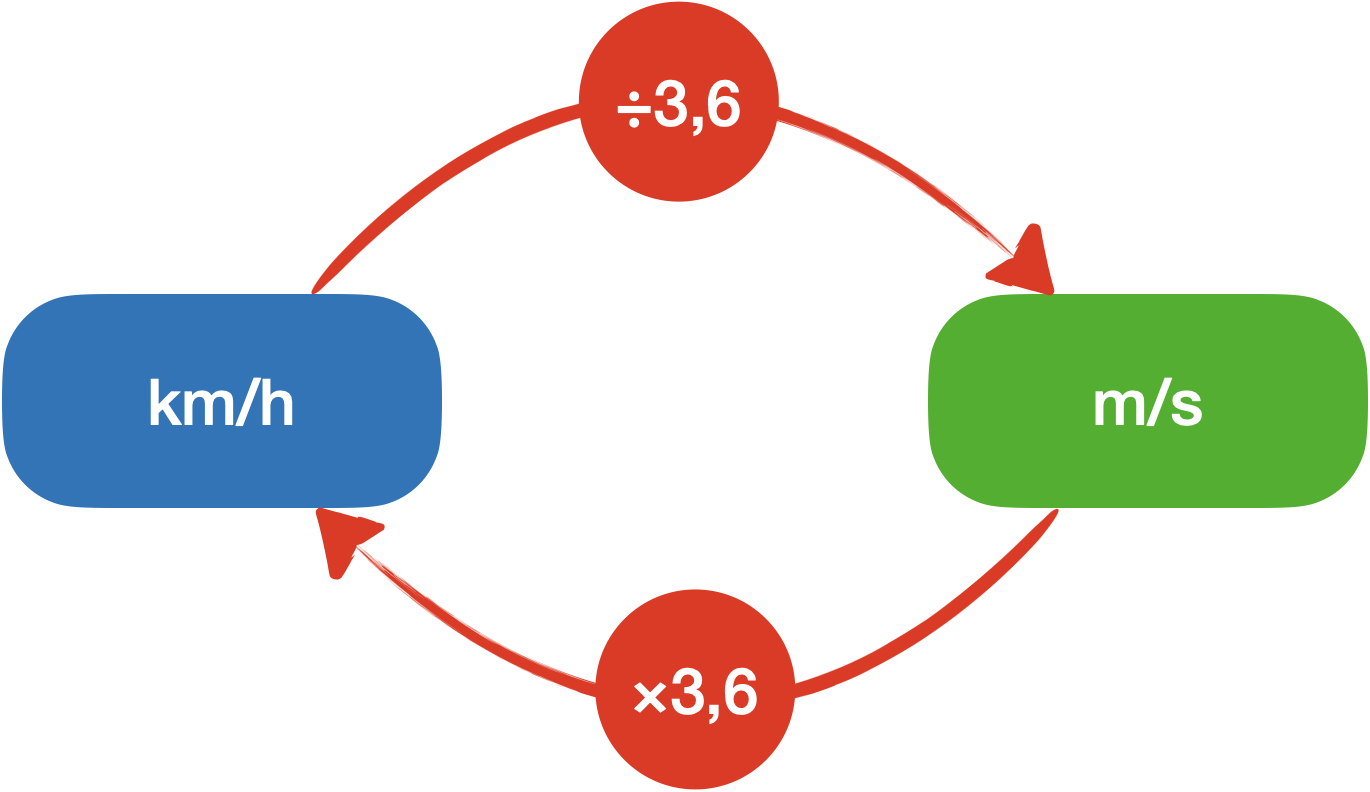
Il faut donc diviser par 3,6
pour passer des km/h aux m/s.
Que doit-on alors faire pour passer des m/s aux km/h ?
Rappel :
En appelant $d$ la distance parcourue (en m)
et $\Delta t$ la durée écoulée (en s),
la vitesse $v$ d’un signal est
donnée par la relation :
Rq :
On écrit $\Delta t$ car une durée est l’écart entre deux instants et le symbole $\Delta$ (Delta) symbolise, en physique, un écart : $\Delta t = t_{final} - t_{initial}$.
Symétriquement, on peut aussi considérer
la distance comme un écart entre deux positions
et au lieu de $d$, on aurait pu écrire $\Delta x$.
Si on connaît la vitesse et la durée,
comment obtient-on la distance ?
Et si on connaît la distance et la vitesse,
comment obtient-on la durée ?
Pourquoi doit-on compter approximativement 3 s
par km entre l'éclair et le tonnerre ?
Qu’est-ce que cette vidéo
nous permet de déterminer ?
Pour augmenter l’intensité du son émis,
beaucoup d’instruments et d’êtres vivants
sont dotés d’une caisse de résonance
qui amplifie et sélectionne les sons.
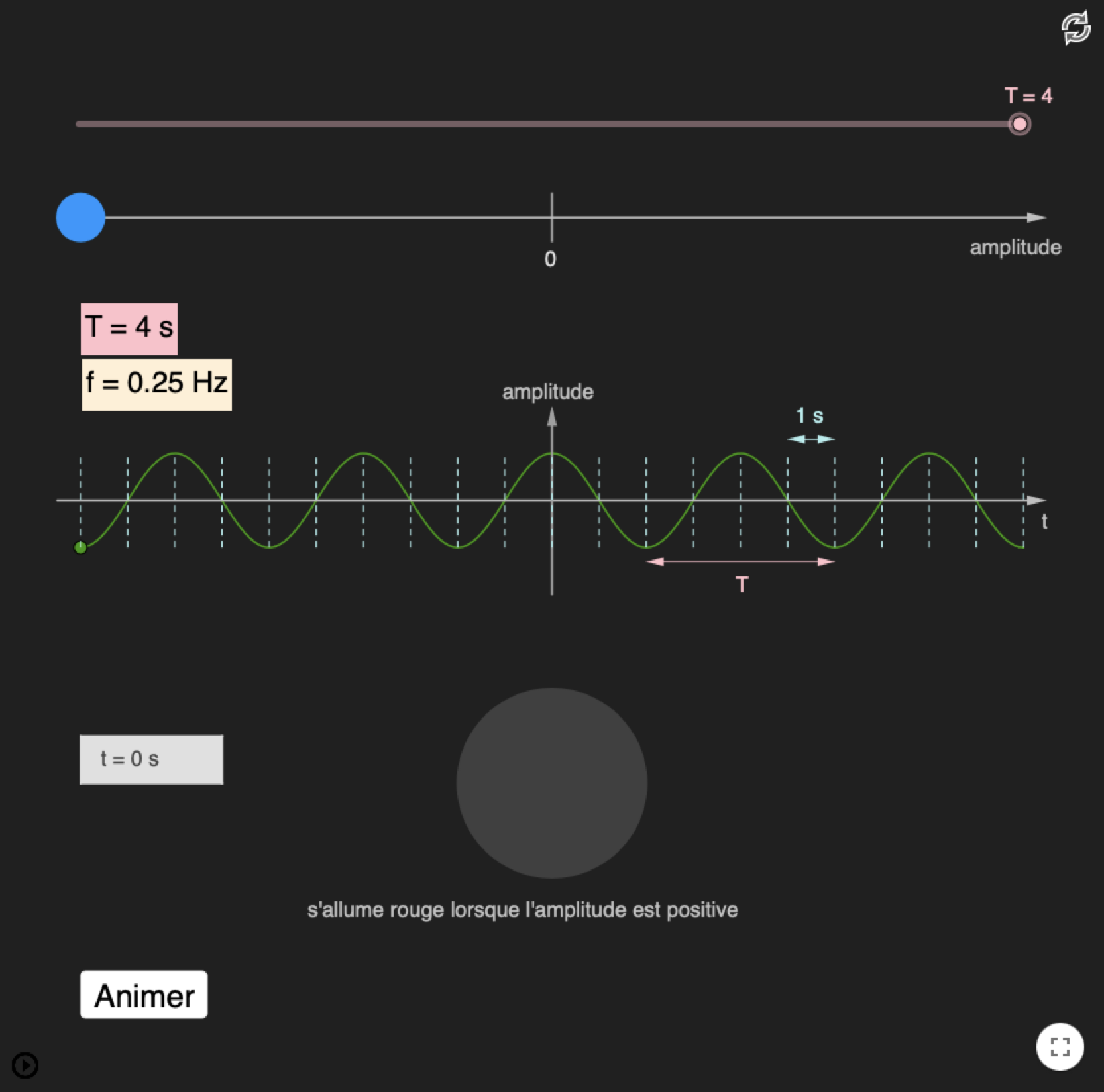
Signal sonore périodique
Les sons musicaux sont des signaux périodiques.
Un signal périodique est un signal
qui se répète à l'identique dans le temps.
La période $T$ d'un signal périodique
est la durée d'une répétition (d'un motif).
Unité : la seconde
Pour des sons musicaux, la période est souvent très petite, de l’ordre de la cs ou ms. On lui préfère alors
le nombre de répétitions (de motifs) par seconde
qui est l’inverse de la période et qu’on appelle
la fréquence $f$.
Unité : le hertz (Hz)
Quelle est la période et la fréquence de ce signal ?
🫀
Quand on “prend son pouls”,
mesure-t-on une période ou une fréquence ?
Perception d’un son
Fréquence : Hz
Volume :
Le domaine des fréquences des sons audibles
pour l’oreille humaine est situé entre 20 et 20000 Hz.
Pour un son musical, la hauteur désigne la note jouée (plus ou moins grave ou aigüe).
La hauteur est liée à la fréquence :
plus la fréquence est grande,
plus la hauteur est grande
et plus la note est aigüe.
Le signal de deux notes identiques jouées par des instruments différents possède la même période
mais la forme des signaux est différente.
On appelle timbre ce qui distingue
deux notes de même hauteur.
Enfin, la troisième caractéristique
d’un son est son intensité.
L'intensité sonore est proportionnelle
à l'amplitude du signal
(une amplitude n fois plus grande
multiplie par n l'intensité sonore).
Si l’intensité sonore de la trompette seule vaut $I_0$
à une certaine distance, alors l’intensité des 4 trompettes jouées ensemble vaudra $4I_0$
à la même distance.
Mais cette relation de proportionnalité rend mal compte de notre sensation auditive.
On peut par exemple mesurer que l'amplitude du son émis par quelqu'un qui parle fort est environ 10 000 fois plus grande que celle d'une personne qui chuchote à la même distance ! Pourtant, on n'a
pas la sensation d'un son 10 000 fois plus fort...
Amplitude et sensation auditive
ne sont pas proportionnelles !
Pour tenir compte de cette échelle non proportionnelle, on utilise une autre grandeur :
le niveau sonore, mesuré en décibels (dB).
Lorsque l'intensité sonore augmente, le niveau sonore augmente aussi, mais beaucoup moins vite.
Durée limite d’exposition (sans protection)
avant dommages :
- de 120 à 140 dB, quelques secondes suffisent à provoquer des dégâts irréversibles ;
- 95 dB : 15 min / jour ;
- 86 dB : 2h / jour ;
- 80 dB : 8h / jour.