Comment faire pour réussir
cette rotation de 90° en place ?

Remarque : en place ne veut pas dire
qu’on ne peut pas créer de variables !
Tant que leur nombre est fixe,
cela ne change pas la complexité en espace.

Une solution possible :

def rotate_in_place(matrix):
    n = len(matrix)
    for r in range(n//2):
        for c in range(r,n-1-r):
            hg = matrix[r][c]
            hd = matrix[c][n-r-1]
            bd = matrix[n-r-1][n-c-1]
            bg = matrix[n-c-1][r]
            matrix[c][n-r-1] = hg
            matrix[n-r-1][n-c-1] = hd
            matrix[n-c-1][r] = bd
            matrix[r][c] = bg

Pour atteindre le niveau “advanced” :

def solution(nums):
    Sanszeros = [pazero for pazero in nums if pazero] 
    return Sanszeros + (len(nums)-len(Sanszeros))*[0]

Pour “legend”, il faut réussir à travailler en place :

def solution(nums):
    n = len(nums)
    iav, iap = 0, 0
    while iap<n:
        if nums[iap]:
            nums[iap],nums[iav] = nums[iav],nums[iap]
            iap += 1
            iav += 1
        else:
            while iap<n and nums[iap]==0:
                iap += 1
    return nums

Précision pour 2^e question :
le challenge a été lancé le 20 septembre 2022.

Solutions possibles :

1. nombre de submissions par langage

SELECT language, COUNT(problem_id) AS lang_count
FROM submissions
GROUP BY language;

2. Joueurs de 25 ans

SELECT nickname 
FROM players
WHERE birth < "1997-09-20" AND birth >= "1996-09-20";

3. Les 10 joueurs ayant présenté
   le plus de problèmes.

SELECT nickname, COUNT(problem_id) AS problem_attempted
FROM (SELECT DISTINCT user_id, problem_id FROM submissions) AS pbunique
JOIN players ON pbunique.user_id = players.user_id
GROUP BY nickname
ORDER BY problem_attempted DESC
LIMIT 10;

4. Les joueurs ayant tenté le même problème
   avec au moins deux langages.

Avec autojointure :

SELECT nickname
FROM
(SELECT DISTINCT sub1.user_id
FROM (SELECT *
FROM submissions) AS sub1
JOIN
(SELECT *
FROM submissions) AS sub2
ON sub1.problem_id = sub2.problem_id and sub1.user_id = sub2.user_id and sub1.language <> sub2.language) AS tablex, players
WHERE tablex.user_id = players.user_id

Une solution assez différente utilisant
un GROUP BY sur plusieurs attributs :

SELECT DISTINCT nickname
FROM
(SELECT user_id, COUNT(language) AS nb_language
FROM
(SELECT DISTINCT user_id, problem_id, language
FROM submissions) AS tab1
GROUP BY user_id, problem_id
HAVING nb_language > 1) AS tab2
JOIN players ON players.user_id = tab2.user_id

5. Joueurs ayant passé au moins 60%
   des problèmes MEDIUM et HARD
   avec un score de 100%.

SELECT nickname
FROM
(SELECT user_id,COUNT(*) AS nombre
FROM ((SELECT DISTINCT problem_id, user_id FROM submissions WHERE score = 100) AS sub1
JOIN (SELECT * FROM problems WHERE (problems.difficulty = "MEDIUM" OR problems.difficulty = "HARD")) AS prob1
ON sub1.problem_id = prob1.problem_id)
GROUP BY user_id) AS tablex
JOIN players
ON players.user_id = tablex.user_id
WHERE tablex.nombre >= 60

Autre possibilité (assez proche) :

SELECT nickname
FROM (SELECT nickname, COUNT(*) AS nbproblem
FROM 
(SELECT DISTINCT nickname, submissions.problem_id
FROM submissions
JOIN problems ON submissions.problem_id = problems.problem_id
JOIN players ON submissions.user_id = players.user_id
WHERE submissions.score = 100 AND (problems.difficulty = "HARD" OR problems.difficulty = "MEDIUM")) AS tab1
GROUP BY nickname
HAVING nbproblem >= 60) AS tab2

Complexité de find_quadruplet_sum ?

def find_quadruplet_sum_fast(numbers, target):
    sommesdeuxadeux = {}
    for a in numbers:
        for b in numbers:
            sommesdeuxadeux[a+b] = (a,b)
    for a in numbers:
        for b in numbers:
            if target - (a+b) in sommesdeuxadeux:
                return (a,b) + sommesdeuxadeux[target - (a+b)]

Complexité de find_quadruplet_sum_fast ?
(recherche dans un dictionnaire via in en O(1))

Une version plus simple du problème :

Algo naïf quadratique :

def test_naif(L,k):
    for i in range(len(L)-1):
        for j in range(i+1,len(L)):
            if L[i]+L[j] == k:
                return True
    return False

Comment passer à une complexité linéaire ?

Avec un dictionnaire pardi !

def test_lin(L,k):
    dico = {}
    for e in L:
        if k-e in dico:
            return True
        dico[e] = True
    return False

En réalité, on se sert ici du dictionnaire comme d’un ensemble (l’association clé-valeur ne nous intéresse pas, on veut seulement savoir si la clé est présente).

Or l’ensemble est une structure de données native
en Python (mais pas au programme).

L’ensemble est une collection non ordonné d’éléments uniques (tout comme il ne peut y avoir deux clés identiques dans un dictionnaire).

{'a',2.18,7} est un ensemble
(c’est donc bien une sorte de dictionnaire
ne contenant que des clés).

Comme dans un dictionnaire, la recherche
dans un ensemble se fait en temps constant.

Remplacer le dictionnaire par un ensemble
dans test_lin donne :

def test_lin(L,k):
    Vu = set() # Vu est un ensemble vide
    for e in L:
        if k-e in Vu:
            return True
        Vu.add(e) # pour ajouter un élément
    return False

Les ensembles sont très pratiques
lorsqu’on a besoin d’éliminer des doublons.

Ainsi, set([1,2,3,1,2,5]) renvoie {1,2,3,5}.

Implémenter cette version
“dance hongroise” du tri rapide
en s’assurant que le tri créé
est bien en place.

Une possibilité :

def partition(L):
    p = 0         # pivot (chapeau noir)
    i = len(L)-1  # chapeau rouge
    while i != p:
      if (L[p]-L[i])*(p-i) < 0:
        L[p],L[i] = L[i],L[p]
        p,i = i,p
      i -= (i-p)//abs(i-p)
    return p
    
def trirapide(L):
    if len(L) <= 1:
      return L
    else:
      p = partition(L)
      L[:p] = trirapide(L[:p])
      L[p+1:] = trirapide(L[p+1:])
      return L

1. Que retourne path_search(6,3,GRAPH) ?
2. Pourquoi le programme n’est-il pas correct ?
3. Qu’est-ce qui, dans le graphe, pose problème ?
4. Pourquoi le chemin entre 6 et 5
   est-il quand même bon ?
5. Réparer le programme pour le rendre correct.
6. Le chemin donné est-il le plus court ?
   Si non, comment faire pour qu’il le soit ?

Il manque dans ce code un registre des sommets déjà visités pour éviter d’y retourner
dans le cas de cycles 😵‍💫.

$6\rightarrow 5$ passe par le cycle $1\leftrightarrow 2$ mais comme
on avance en profondeur et que l’ordre des successeurs de 2 dans le graphe est [5,4,1],
on évite de boucler 😅.

Pour ne pas changer de classe de complexité,
l’idée est d’utiliser un dictionnaire dans lequel
on ajoutera chaque sommet visité.

On profite alors du fait que la recherche d’une clé dans un dictionnaire (if key in dico :)
se fait en temps constant ($(O(1)$) 🥳.

Code modifié :

def path_search(start, end, graph, vus=None):
    if vus is None : # explication slides suivantes
        vus = {}
    vus[start]=True
    if start == end:
        return [start]
    if graph[start] == []:
        return None
    for neighbor_node in graph[start]:
        if not neighbor_node in vus:
            path = path_search(neighbor_node, end, graph, vus)
            if path is not None:
                return [start] + path

vus = None ?

L’idée première est d’utiliser l’argument nommé :
vus = {}.

Un argument nommé permet d’avoir une valeur
par défaut pour l’argument qui n’est alors
plus nécessaire lors de l’appel.

Exemple :

def presentation(prenom,nom,job="sans") :
	print(f"identité : {prenom} {nom}, activité : {job}")

>>> presentation("Alan","Turing","génie")
identité : Alan Turing, activité : génie

>>> presentation("John","Doe")
identité : John Doe, activité : sans

Comme il n’ y a pas de 4^e argument dans le test,
et que modifier le test pourrait passer pour de la triche, les arguments nommés semblent
être une bonne solution.

Mais on se confronte alors à l’un des plus vicieux problèmes que peuvent poser les objets mutables
en python, à chaque fois que l’argument par défaut est appelé, le même objet est utilisé !

Exemple :

def vicieux(L=[]):
	L.append(1)
	return L

>>> vicieux([0])
[0,1]

Normal.

>>> vicieux()
[1]

C’est bien ce qu’on voulait…

Mais que renvoit un nouveau vicieux() ?

>>> vicieux()
[1,1]

🤯

Et du coup, ça fiche en l’air notre stratégie !
car à chaque test, le même dictionnaire
des sommets visités va être utilisé
et il sera donc tout à fait inutile.

La bidouille pour se sauver est d’utiliser None
comme valeur par défaut afin de s’en servir comme test de premier appel pour initialiser l’objet mutable.

Rq : plutôt que None, on aurait pu utiliser un entier
ou une chaîne de caractères, c’est juste plus propre
et logique avec None (l’objet n’existe pas encore).

Exemple avec une chaîne de caractères :

def path_search(start, end, graph, vus="init"):
    if vus == "init" :
        vus = {}
    vus[start]=True
    if start == end:
        return [start]
    if graph[start] == []:
        return None
    for neighbor_node in graph[start]:
        if not neighbor_node in vus :
            path = path_search(neighbor_node, end, graph, vus)
            if path is not None:
                return [start] + path

Ça passe tout aussi bien les tests.

À propos des tests :

for a, b in zip(result, result[1:]):
	# Iterate over all consecutive pairs
	# Super helpful Python trick using zip :)
	assert b in graph[a]

Cela permet de tester ici qu’un sommet est bien un successeur du sommet qu’il suit dans la liste retournée par la fonction.

Comment aurait-on fait sans cette astuce ?

Un algo naïf serait :

def produitsaufi(L):
    n = len(L)
    L_sortie = []
    for i in range(n):
        p = 1
        for j in range(n):
            if j != i:
                p *= L[j]
        L_sortie.append(p)
    return L_sortie

Peut-on faire mieux que cette
complexité quadratique ?

Oui :

def produitsaufi(L):
    n = len(L)
    p = 1
    for i in range(n):
        p *= L[i]
    return [p//L[i] for i in range(n)]

Mais si on vous demande de garder
une complexité linéaire tout en vous
interdisant les divisions ?

On peut utiliser deux listes L_gauche et L_droite qui vont contenir les produits à gauche et à droite de i

• L_gauche[i] = $\prod_{j=0}^{i-1}$L[j]
• L_droite[i] = $\prod_{j=i+1}^{n-1}$L[j]

On aura bien ainsi :
L_gauche[i]*L_droite[i] = $\displaystyle \prod_{\substack{j=0\\j≠i}}^{n-1}$L[j]

def produitsaufi(L):
    n = len(L)
    L_gauche = [1]*n
    L_droite = [1]*n
    for i in range(1,n):
        L_gauche[i] = L[i-1]*L_gauche[i-1]
    for i in range(n-2,-1,-1):
        L_droite[i] = L[i+1]*L_droite[i+1]
    return [L_gauche[i]*L_droite[i] for i in range(n)]

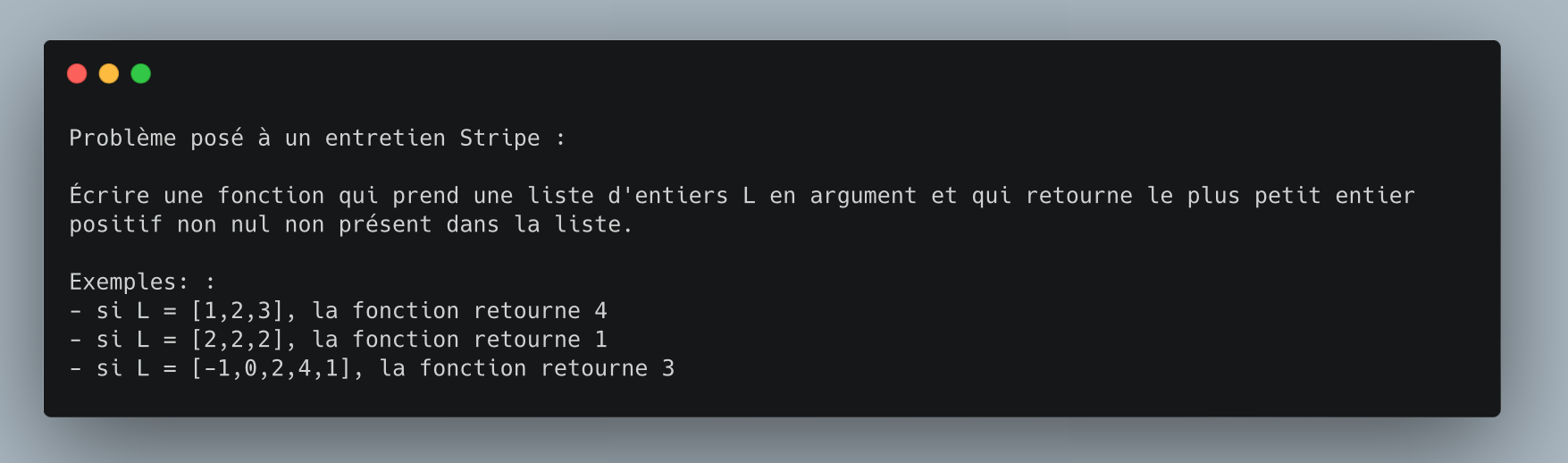
Un 1^er algo :

def pluspetitpasla(L):
    n = len(L)
    i = 1
    while i < n+1:
        if i not in L:
            return i
        else:
            i += 1
    return n+1

Complexités ?

spatiale : $O(1)$
temporelle : $O(n^2)$

def pluspetitpasla(L):
    n = len(L)
    i = 1
    while i < n+1: # O(n)
        if i not in L: # O(n)
            return i
        else:
            i += 1
    return n+1

Un algo linéaire en place:

def pluspetitpasla(L):
    n = len(L)
    i = 0
    while i < n:
        if 1 <= L[i] < n and L[L[i]-1] != L[i]: # la 2e condition évite de boucler à l'infini
            L[L[i]-1], L[i] = L[i], L[L[i]-1]
        else:
            i += 1
    for i in range(n):
        if L[i] != i+1:
            return i+1
    return n+1

Prouver la correction totale de l’algorithme

• Pour la terminaison, il faut prouver que la condition du while est toujours rencontrée :
  $n-i$ est un variant de boucle :
  
  • $n-i>0$ par la condition du while
  • pour prouver que $n-i$ est strictement décroissante, on va prouver qu’on ne peut pas être bloqué plus de $n$ itérations
    sur le if :

• Pour la correction partielle, l’invariant qu’on cherche à maintenir dans la boucle while est :

L[L[j]-1]$=$L[j] si L[j]$≤$n
pour tout $j≤i$
$\equiv$
Chaque élément L[j]$≤$ n
a été placé à la position correspondant à sa valeur

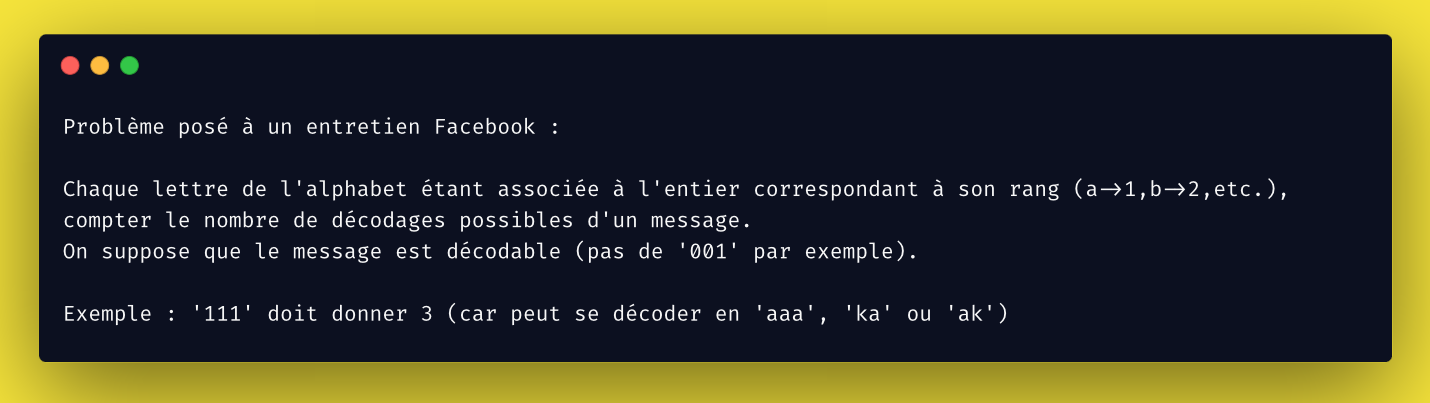
Faisons aussi s’afficher les différents mots décryptés
pour que cela soit plus parlant.

La récursivité semble une voix prometteuse puisqu’il s’agit de compter toutes les branches possibles aboutissant à un mot différent en partant de la racine commune que représente le message initial.

Construisons d’abord pour nos tests le dictionnaire permettant de décoder et le dictionnaire inverse permettant l’encodage.

alphabet = "abcdefghijklmnopqrstuvwxyz"
decode = {i:alphabet[i-1] for i in range(1,27)}
encode = {val:str(key) for key,val in decode.items()}

message = "athlete"
crypt = ""
for c in message:
  crypt += encode[c]
crypt

‘1208125205’

La fonction récursive construisant
et comptant les mots différents :

def nbdemotsdiff(mess,i=0,mot=""):
  global compt
  n = len(mess)
  if i > n-1:
    compt += 1
    print(mot)
    return mot
  if mess[i] == "0":
    return
  if i != n-1 and (mess[i] == "1" or (mess[i] == "2" and int(mess[i+1]) <= 6)):
    nbdemotsdiff(mess,i+1,mot+decode[int(mess[i])])
    nbdemotsdiff(mess,i+2,mot+decode[int(mess[i:i+2])])
  else:
    nbdemotsdiff(mess,i+1,mot+decode[int(mess[i])])

Exemple :

compt = 0
nbdemotsdiff("1208125205")
print(compt)

On obtient :
athabete
athayte
athlete
3

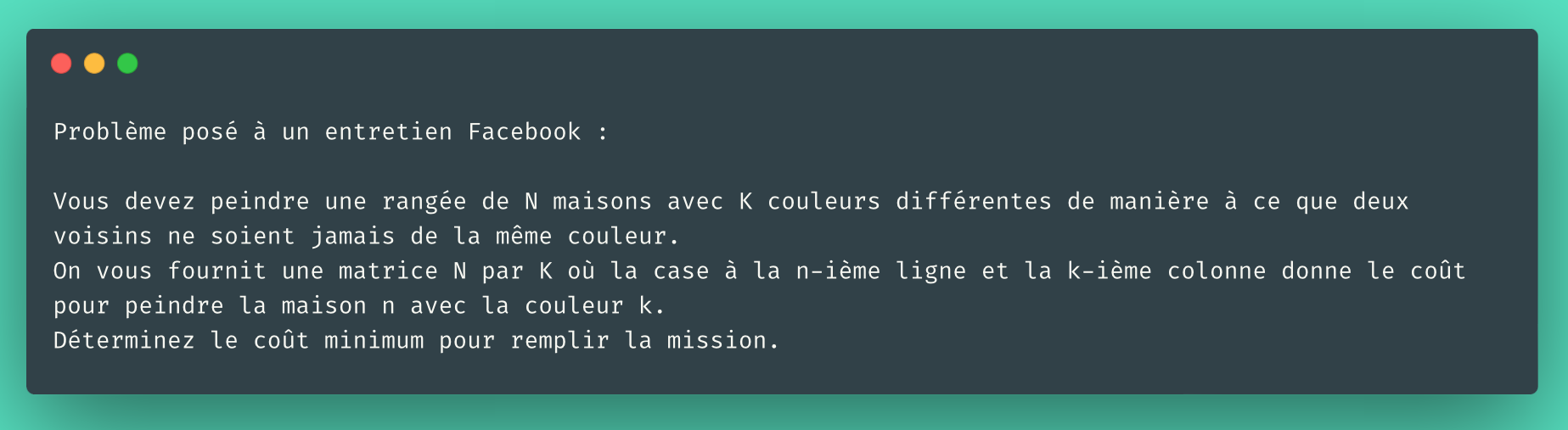
C’est typiquement un problème
pour la programmation dynamique :

L’idée va être de construire une matrice N par K
où on trouve à la ligne n le coût minimal
pour peindre la maison n de la couleur k
et toutes les maisons qui précèdent.

La première ligne de la matrice correspond simplement aux coûts pour peindre la première maison dans les k couleurs différentes.

Supposons que la ligne n donne bien pour chaque couleur de la maison n le coût total minimal
pour peindre les n premières maisons.

La case k de la ligne n+1 s’obtient alors en prenant
le coût pour peindre la maison n+1 de la couleur k auquel on ajoute le plus petit coût de la ligne n
pour toutes les couleurs autres que k.

On s’assure bien ainsi du coût total optimal
pour chaque couleur de la maison n+1 !

Une fois la matrice construite, on obtient le coût total minimal final en prenant la valeur minimale
de la dernière ligne.

def cout_tot_min(mat_couts):
  N = len(mat_couts)
  K = len(mat_couts[0])
  M_tot = [[0]*K for i in range(N)]
  for k in range(K):
    M_tot[0][k] = mat_couts[0][k]
  for n in range(1,N):
    for k in range(K):
      M_tot[n][k] = mat_couts[n][k] + min([M_tot[n-1][kprime] for kprime in range(K) if kprime != k])
  return min(M_tot[n-1])

Complexité ?

$O(NK^2)$

On peut aussi s’amuser à déterminer les couleurs
avec lesquelles il faut peindre chaque maison
pour aboutir au coût minimum.

Faisons d’abord retourner par cout_tot_min la matrice construite en plus du coût total minimal :

return min(M_tot[n-1]),M_tot

Il n’y a plus ensuie qu’à “remonter” la matrice…

def reconstruction(M_tot,mat_couts,Lcouleurs):
  N = len(M_tot)
  K = len(M_tot[0])
  Couleurs_maisons = [""]*N
  Min = min(M_tot[N-1])
  for n in range(N-1,-1,-1):
    k = 0
    while M_tot[n][k] != Min:
      k += 1
    Couleurs_maisons[n] = Lcouleurs[k]
    Min = Min - mat_couts[n][k]
  return Couleurs_maisons

Exemple :

Mcoutpeinture = [[2000,2500,3000,1500],
                 [4000,4500,1500,2000],
                 [2800,3900,4200,3000],
                 [1500,1800,2000,1200],
                 [1000,2000,1400,1500],
                 [5000,3500,7000,4000]]

Couleurs = ["Rouge","Vert","Bleu","Jaune"]

coutmin,M_tot = cout_tot_min(Mcoutpeinture)
print(coutmin)
print(reconstruction(M_tot,Mcoutpeinture,Couleurs))

11500
[‘Jaune’, ‘Bleu’, ‘Rouge’, ‘Jaune’, ‘Rouge’, ‘Vert’]

Problèmes classiques :

• Trouver une ou toutes les solutions au problème des 8 dames (ou n dames).
• Trouver la solution d’une grille de sudoku.

Dans les deux cas, l’utilisation du backtracking
donne des codes plutôt élégants :