Méthode d’Euler

On cherche à résoudre numériquement
une équation différentielle.

Plus précisément, on cherche la solution
au problème de Cauchy suivant :

L’idée générale est de discrétiser le temps
par un pas $h$ tel que $t_{i+1}=t_i + h$
et d’utiliser $f(t,y)$ pour approximer
$y(t_{i+1})$ à partir de $y(t_i)$.

Méthode d’Euler explicite

Dans cette méthode, on utilise la pente au point de départ pour obtenir le point d’arrivée :

Méthode d’Euler implicite

Dans cette méthode, on utilise la pente au point d’arrivée pour obtenir le point d’arrivée :

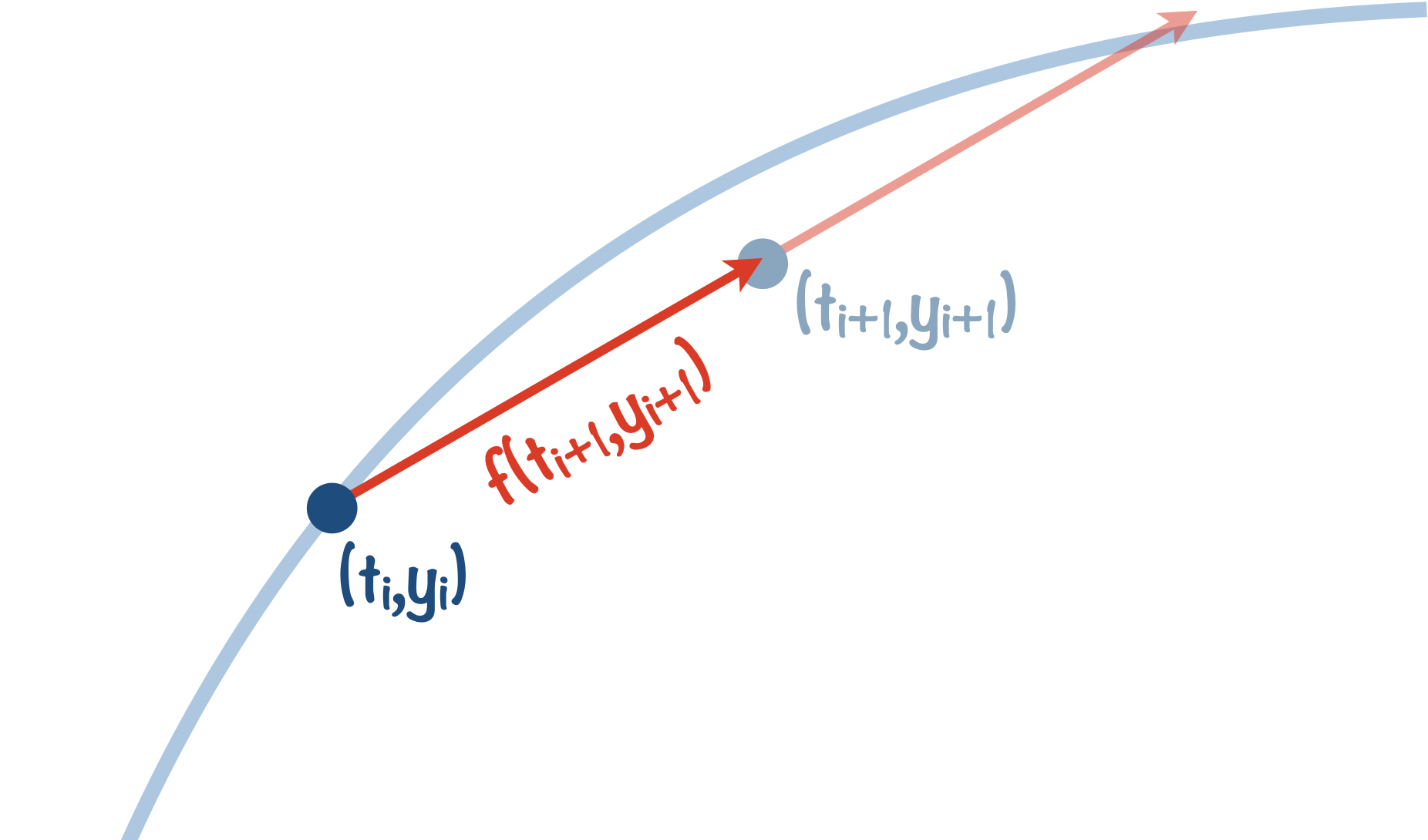
La méthode implicite demande plus de calculs puisqu’on souhaite utiliser $y_{i+1}$
pour déterminer $y_{i+1}$.

$\Rightarrow$ on se retrouve avec une équation à résoudre…

Dans notre exemple :

$$ \begin{aligned} y_{i+1} &= y_i + h\times f(t_{i+1},y_{i+1})\\ &= y_i + h\times \frac{y_\infty-y_{i+1}}{\tau} \end{aligned} $$ D’où

$$ \displaystyle y_{i+1}= \frac{y_i + \frac{hy_\infty}{\tau}}{1+\frac{h}{\tau} } $$

Equa diff d’ordre > 1

Pour gérer une équa diff d’ordre $n$,
on la transforme en un système de $n$ équa diff d’ordre 1 en définissant une nouvelle variable
pour chaque $y^{(i)}$ pour $i\in\{1\ldots n-1\}$

Exemple :

l’équation d’un oscillateur amorti

$$ \ddot{x}(t) = -\frac{k}{m}(x(t)-l_0)-\frac{\alpha}{m} \dot{x}(t) $$

devient :

$$ \begin{cases} \dot{x}(t) = v(t) \\ \dot{v}(t) = -\frac{k}{m}(x(t)-l_0)-\frac{\alpha}{m} v(t) \end{cases} $$

Erreur de troncature locale

C’est la petite erreur faite à chaque étape.

De $(t_0,y_0)$ à $(t_1,y_1)$ avec $t_1 = t_0+h$,
la solution numérique donne :

$y_1 = y_0 + hf(t_0,y_0)$

Et la solution exacte (développement de Taylor) :

$y(t_1) = y(t_0) + hy’(t_0) + \frac{1}{2}h^2 y’’(t_0)+O(h^3)$

D’où une erreur $|y_1-y(t_1)|$ en $\color{red}O(h^2)$.

Erreur de troncature globale

C’est l’accumulation des erreurs locales de $t_0$ à $t$.

Nombre d’étapes : $\lfloor \frac{t-t_0}{h}\rfloor$ $\Rightarrow$ en $O(1/h)$.
D’où une erreur de troncature globale en $O(h)$.

C’est pour cette erreur linéaire en $h$
que la méthode d’Euler (explicite ou implicite)
est dite d’ordre 1.

Erreur d’arrondi

Explique pourquoi diminuer $h$ finit par ne plus apporter de précision supplémentaire.

x = 1.0
p = 0
while x != x+1 :
	x *= 2
	p += 1
print(x)
print(p)

Le code ci-dessous trouve la première puissance de 2, $x$, pour laquelle $x+1$ est arrondi à $x$ (absorption), provoquant une erreur relative
(la plus grande possible) de $1/x$.

l’epsilon machine ou précision machine
est la limite supérieure de l’erreur relative d’approximation causée par l’arrondi.

En python, comme la mantisse d’un flottant correspond à 53 bits, l’errreur relative se fait sur le dernier bit et vaut donc $2^{-53}$ ($\varepsilon=2^{-52}$ au pire entre deux arrondis consécutifs).

Par conséquent, l’erreur d’arrondi sur chaque valeur $y_n$ obtenue par la méthode d’Euler
est de l’ordre de $\varepsilon y_n$.

Et en considérant ces erreurs d’arrondi
comme des variables aléatoires indépendantes,
l’erreur relative d’arrondi totale va être de l’ordre de $\varepsilon\sqrt{n}$ où $n$, le nombre de valeurs calculées,
est inversement proportionnel au pas.

Finalement, l’erreur d’arrondi globale
est proportionnelle à $\frac{\varepsilon}{\sqrt{h}}$
et donc diverge lorsque $h$ tend vers 0 !

Réduire l’erreur de troncature se fait
au détriment de l’erreur d’arrondi.

Néanmoins, on peut se prémunir en bonne part des erreurs d’arrondi grâce à une sommation compensée (algorithme de Kahan).

Stabilité numérique

Partons de l’équation différentielle linéaire $y’=ky$ La méthode explicite donne alors :

$y_{n+1}= y_n(1+hk)$

$\Rightarrow y_n = y_0(1+hk)^n$

la solution numérique ne sera stable que si
$|1+z| ≤ 1$ avec $z \equiv hk \in\mathbb{C}$

En généralisant à un système différentiel linéaire de la forme : $y’(t)=My(t)$
(où $M$ est une matrice carrée)

il faudra, pour obtenir une solution stable,
que chaque valeur propre de $M$
soit dans le disque précédent.

Pour l’exemple de l’oscillateur amorti : $$\begin{pmatrix}\dot{z}_1\\ \dot{z}_2\end{pmatrix}=\begin{pmatrix}0&1\\ -{\omega_0}^2 & -\frac{\omega_0}{Q}\end{pmatrix}\begin{pmatrix}z_1\\ z_2\end{pmatrix}$$

On obtient deux valeurs propres complexes
si $Q>1/2$ : $$\lambda_{\genfrac{}{}{0pt}{}{1}{2}} = \omega_0\left(\frac{1}{2Q} \pm i\sqrt{\left(1-\frac{1}{2Q}\right)^2}\right)$$

et donc pour que $hk=h\lambda_{\genfrac{}{}{0pt}{}{1}{2}}$ soit à l’intérieur
du domaîne de stabilité, il faut que

$\left(-\frac{h\omega_0}{2Q}+1\right)^2 + \left(\frac{h\omega_0}{2Q}\right)^2(4Q^2-1) ≤ 1$.

La domaîne de stabilité
de la méthode d’Euler implicite est
beaucoup plus grand que celui de l’explicite :

il correspond au complément du
disque de rayon 1 centré sur $(1;0)$.

Donc dans le cas de l’oscillateur amorti, toutes les solutions sont stables, quel que soit le pas !

Conservation de l’énergie

Comme on peut le voir sur l’exemple précédent, aucune des deux méthodes ne sait gérer de manière satisfaisante l’oscillateur harmonique !

On dit que ces méthodes ne sont pas symplectiques (elles ne conservent pas l’énergie).

Une solution simple existe :

la métode d’Euler semi-implicite !

C’est aussi une méthode d’ordre 1, mais l’erreur n’est plus maintenant concentrée sur l’amplitude, mais sur la phase.

principe :

on mixe méthode explicite et implicite en utilisant le vieux ${z_2}_i$ pour obtenir ${z_1}_{i+1}$ :

${z_1}_{i+1} = {z_1}_i + h{z_2}_i$

et le nouveau ${z_1}_{i+1}$ pour obtenir ${z_2}_{i+1}$ :

${z_2}_{i+1} = {z_2}_i + hf({z_1}_{i+1},{z_2}_i,t_i)$

Son implémentation est souvent très simple (plus simple même que l’explicite) puisqu’on n’ a même plus besoin des variables z1_old et z2_old :

z1 += h*z2
z2 += h*alpha/m*z2 + h*k/m*(z1-l0)

La méthode semi-implicite peut s’avérer instabe (contrairement à l’implicite).

Méthodes d’ordre supérieur

Ces méthodes permettent d’obtenir une erreur
de troncature globale en $O(h^\text{ordre})$.

Les plus simples à implémenter sont les méthodes de type Runge-Kutta qui consiste à moyenner
les tangentes en différentes positions.

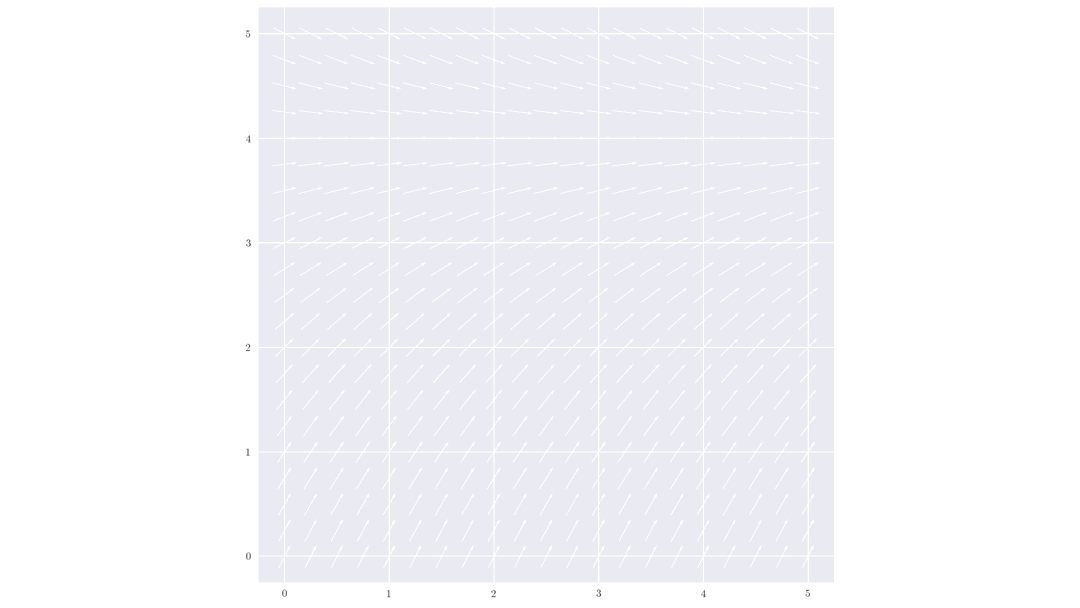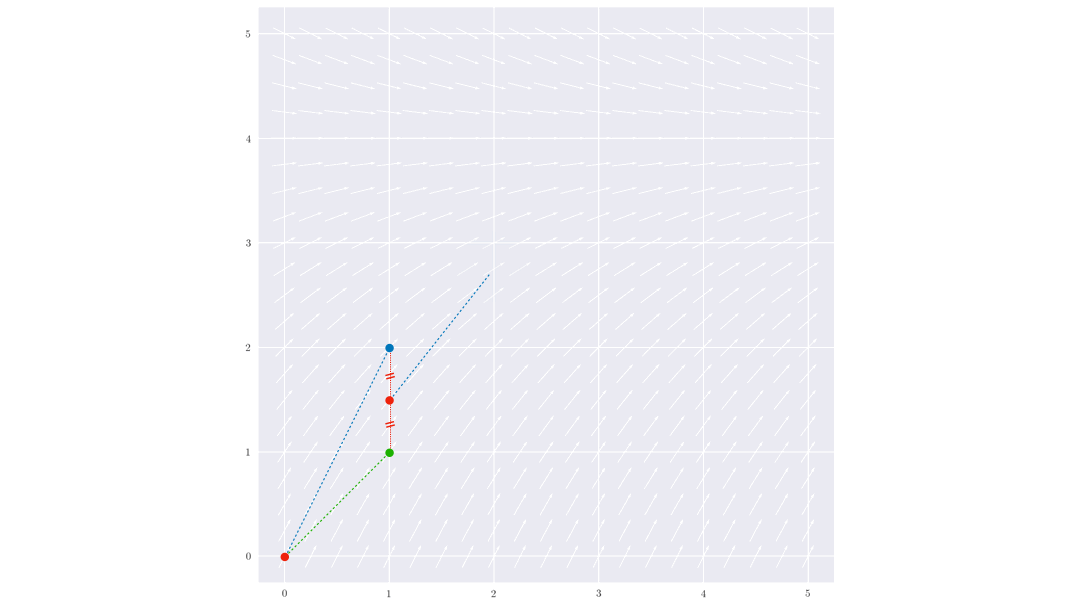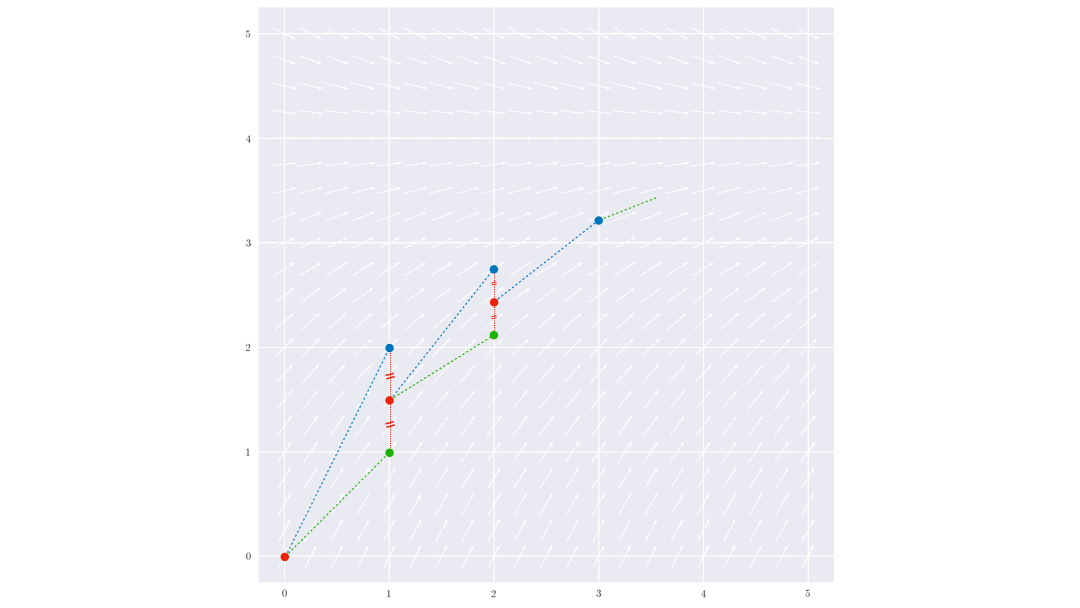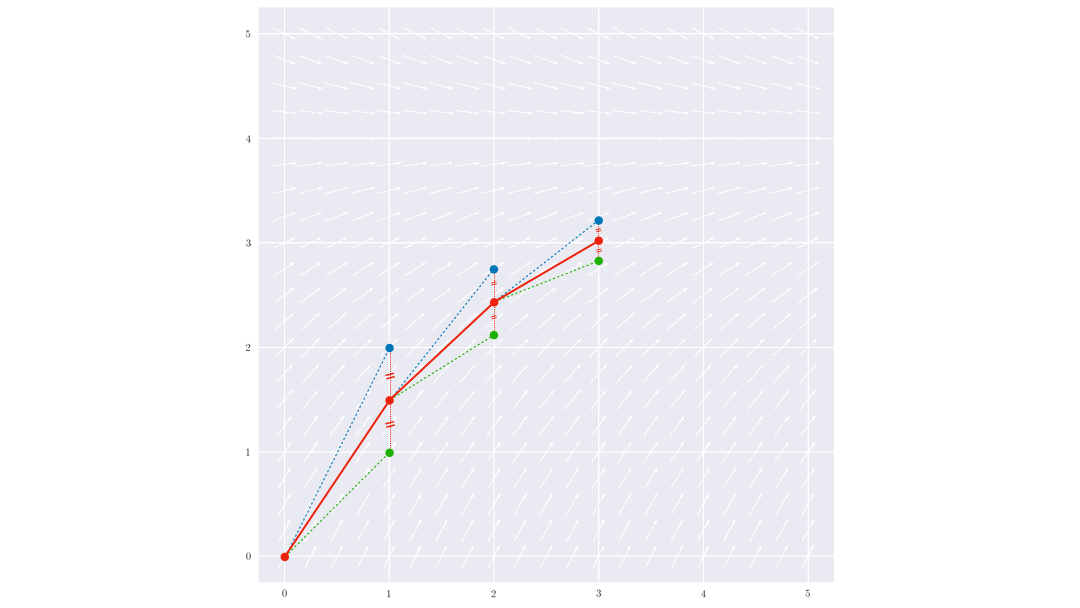
En pratique, les physiciens utilisent le plus fréquement la méthode Runge-Kutta d’ordre 4 (RK4) qui offre un bon compromis entre précision et vitesse (le pas n’a pas besoin d’être très faible pour obtenir des résultats convenables).