Mouvement dans un champ uniforme

Champ de pesanteur uniforme

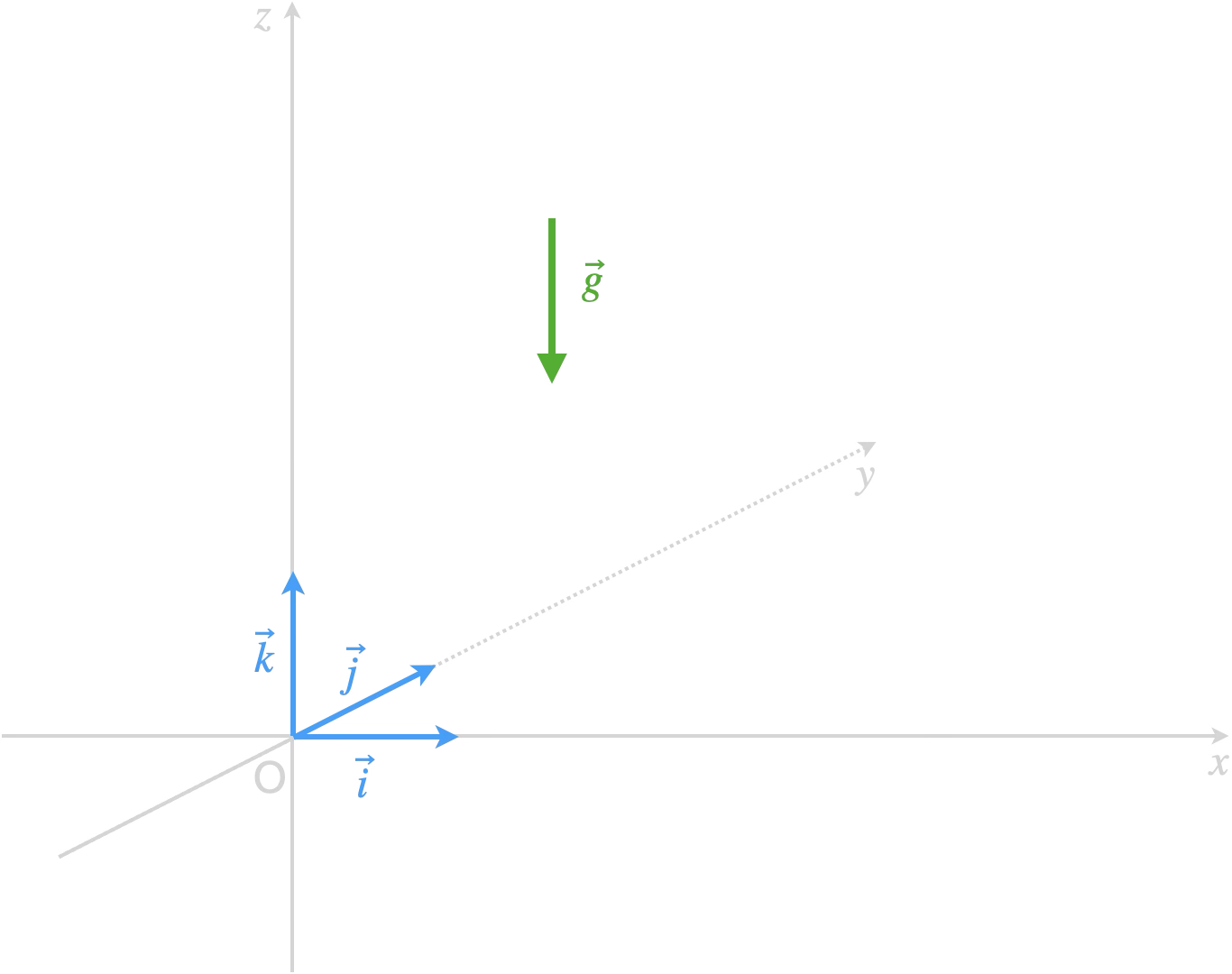
Le champ de pesanteur est décrit par un champ vectoriel $\vec{g}$ dont la direction est indiquée
par un fil à plomb.

Placée dans un champ de pesanteur, toute masse $m$ subit une force $\vec{P}=m\vec{g}$ appelée poids.

La valeur de $g$ varie en fonction
de la position sur Terre et de l’altitude.

Au voisinage de la surface d’une planète, sur des distances faibles par rapport à son rayon, le champ de pesanteur $\vec{g}$ peut être considéré comme uniforme.

Rq : uniforme signifie partout identique ($\vec{g}=\vec{\text{cte}}$).

Équations horaires du mouvement
et équation de la trajectoire

On étudie le lancer d’une balle de basket.

À l'instant $t=0$, la balle quitte les mains du joueur.

On néglige les forces de frottement
$\Rightarrow$ seule force extérieure : le poids
$\Leftrightarrow$ situation de chute libre.

Dans le référentiel terrestre, supposé galiléen,
le mouvement du centre de masse $\mathrm{M}$ d’un système de masse constante $m$ est étudié dans le repère d’espace $(\mathrm{O};\vec{i},\vec{j},\vec{k})$.

Conditions initiales :

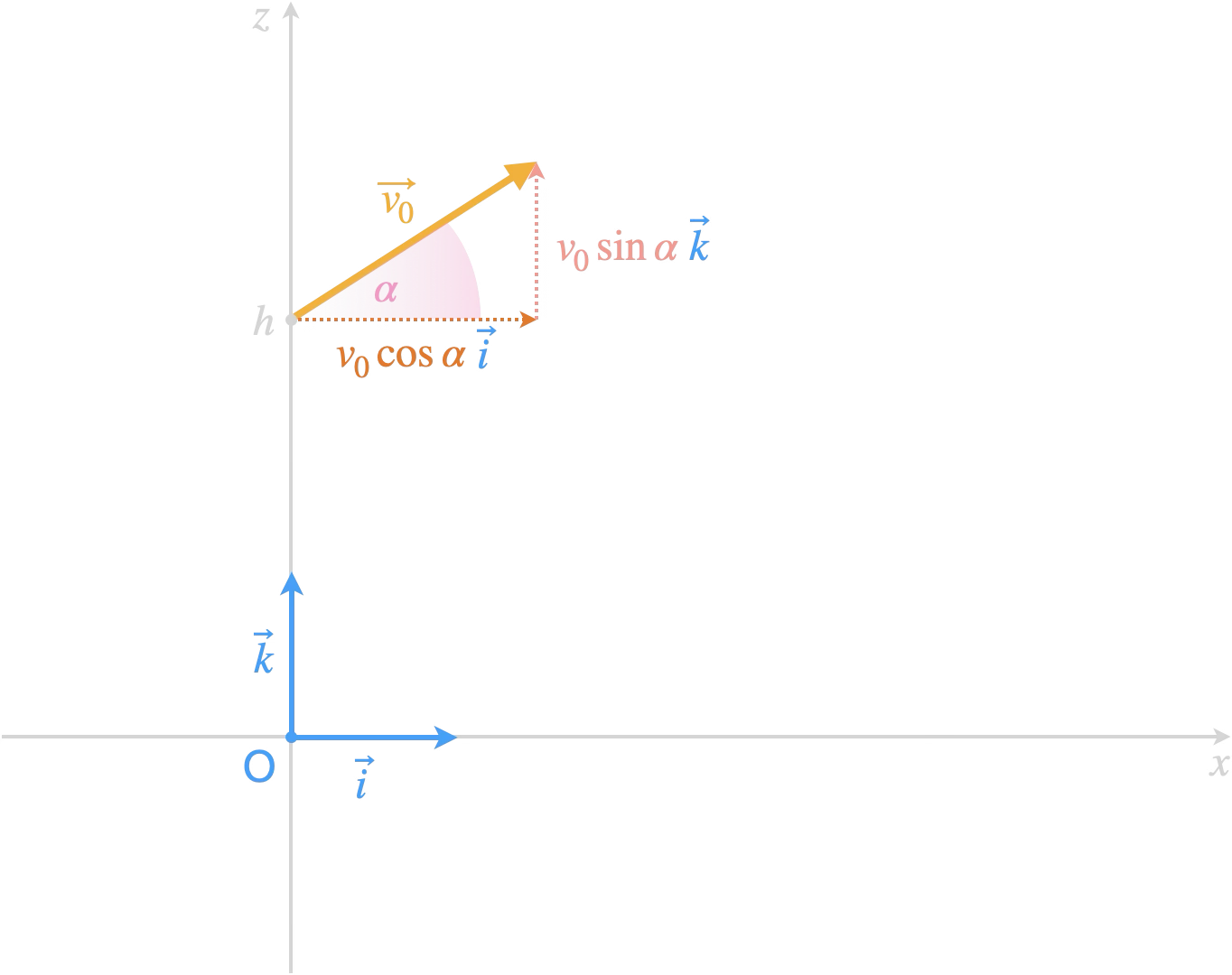
À la date $t=0$, le point $\mathrm{M}$ est situé en $\mathrm{M_0}(0,0,h)$.
Et son vecteur vitesse initial vaut :

$$ \vec{v}(t=0)=\vec{v}_0= \begin{cases} v_x(0)=v_0\cos(\alpha)\\ v_y(0)=0\\ v_z(0)=v_0\sin\alpha \end{cases} $$

Inventaire des forces extérieures

le poids

Vecteur accélération

Application de la deuxième loi de Newton :

$$m{\color{#61D836}\vec{a}} = \sum \color{#FF968D}\vec{F}_\mathrm{ext}$$

$$\Rightarrow m{\color{#61D836}\vec{a}}={\color{#FF968D}m\vec{g}} \Rightarrow {\color{#61D836}\vec{a}}={\color{#FF968D}\vec{g}}$$

Le mouvement est uniformément accéléré vers le bas.

Coordonnées du vecteur accélération :

$$ \vec{a}(t)= \begin{cases} a_x(t)=0\\ a_y(t)=0\\ a_z(t)=-g \end{cases} $$

Vecteur vitesse

Les coordonnées du vecteur vitesse sont des primitives des coordonnées du vecteur accélération.

$ \vec{a}(t)= \begin{cases} \frac{\mathrm{d}v_x}{\mathrm{d}t}=0\\ \frac{\mathrm{d}v_y}{\mathrm{d}t}=0\\ \frac{\mathrm{d}v_z}{\mathrm{d}t}=-g \end{cases} $ $\Rightarrow$ $ \vec{v}(t)= \begin{cases} v_x(t)=c_1\\ v_y(t)=c_2\\ v_z(t)=-gt+c_3 \end{cases} $

Comment obtenir les constantes d’intégration
$c_1$, $c_2$ et $c_3$ ?

Grâce aux conditions initiales :

$v_x(0)=c_1=v_0\cos\alpha$
$v_y(0)=c_2=0$
$v_z(0)=c_3=v_0\sin\alpha$

Coordonnées du vecteur vitesse :

$$ \vec{v}(t)= \begin{cases} v_x(t)=v_0\cos\alpha\\ v_y(t)=0\\ v_z(t)=-gt+v_0\sin\alpha \end{cases} $$

Coordonnées du vecteur position :
équations horaires du mouvement

Les coordonnées du vecteur position sont des primitives des coordonnées du vecteur vitesse.

$ \vec{v}(t)= \begin{cases} \frac{\mathrm{d}x}{\mathrm{d}t}=v_0\cos\alpha\\ \frac{\mathrm{d}y}{\mathrm{d}t}=0\\ \frac{\mathrm{d}z}{\mathrm{d}t}=-gt+v_0\sin\alpha \end{cases} $

$\Downarrow$

$ \overrightarrow{OM}(t)= \begin{cases} x(t)=(v_0\cos\alpha)t+c'_1\\ y(t)=c'_2\\ z(t)=-\frac12 gt^2+(v_0\sin\alpha)t+c'_3 \end{cases} $

On obtient $c’_1$, $c’_2$ et $c’_3$ grâce aux conditions initiales :

$x(0)=c'_1=0$
$y(0)=c'_2=0$
$z(0)=c'_3=h$

D’où les équations horaires

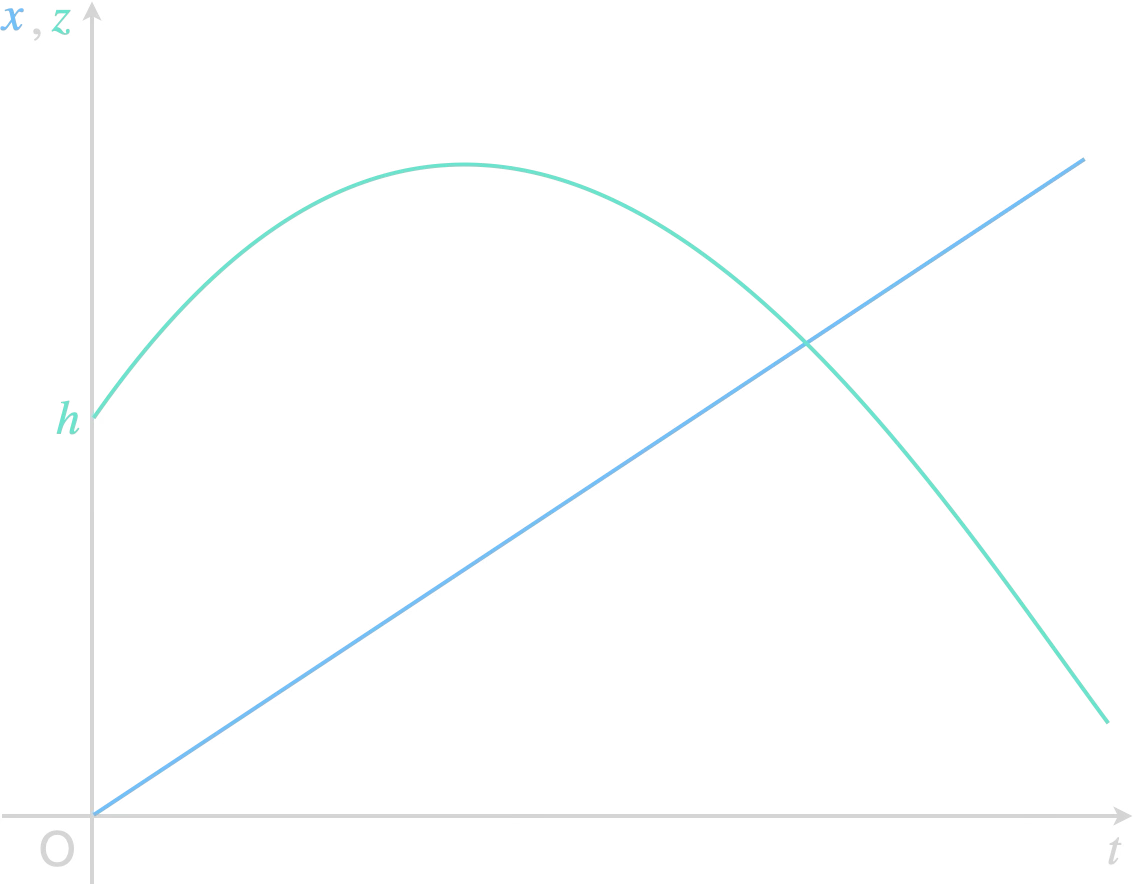
$$ \overrightarrow{OM}(t)= \begin{cases} x(t)=(v_0\cos\alpha)t\\ y(t)=0\\ z(t)=-\frac12 gt^2 + (v_0\sin\alpha)t + h \end{cases} $$

Équation de la trajectoire

Comment obtenir $z(x)$ à partir de $\overrightarrow{OM}(t)$ ?

On isole $t$ grâce à l'équation $x(t)$
On remplace dans $z(t)$.

$x(t) = (v_0\cos\alpha)t$ $\Rightarrow \color{#FF95CA}t=$$\displaystyle \frac{x}{v_0\cos\alpha}$

D'où

$z(x)=$$-\frac12 g \left({\color{#FF95CA}\frac{x}{v_0\cos\alpha}}\right)^2+v_0\sin\alpha\left( {\color{#FF95CA}\frac{x}{v_0\cos\alpha}}\right)+h$

En simplifiant, on obtient l’équation de la trajectoire :

$$ z(x)=-\frac{g}{2\left(v_0\cos\alpha\right)^2}x^2+\left(v_0\tan\alpha\right) x+h $$

La trajectoire est donc plane
(comprise dans le plan $(\mathrm{O},\vec{i},\vec{k})$.

Le mouvement de chute libre est parabolique
(la trajectoire est une portion de parabole).

Le mouvement de chute libre
ne dépend pas de la masse !

En effet, la masse a disparu dès le départ
(2^e loi de Newton).

Petits exercices

Si on néglige les frottements, à quelle hauteur
se trouve approximativement la personne ?

Que peut-on supposer en réalité ?

À quelle vitesse minimale doit partir
la balle pour passer le filet ?

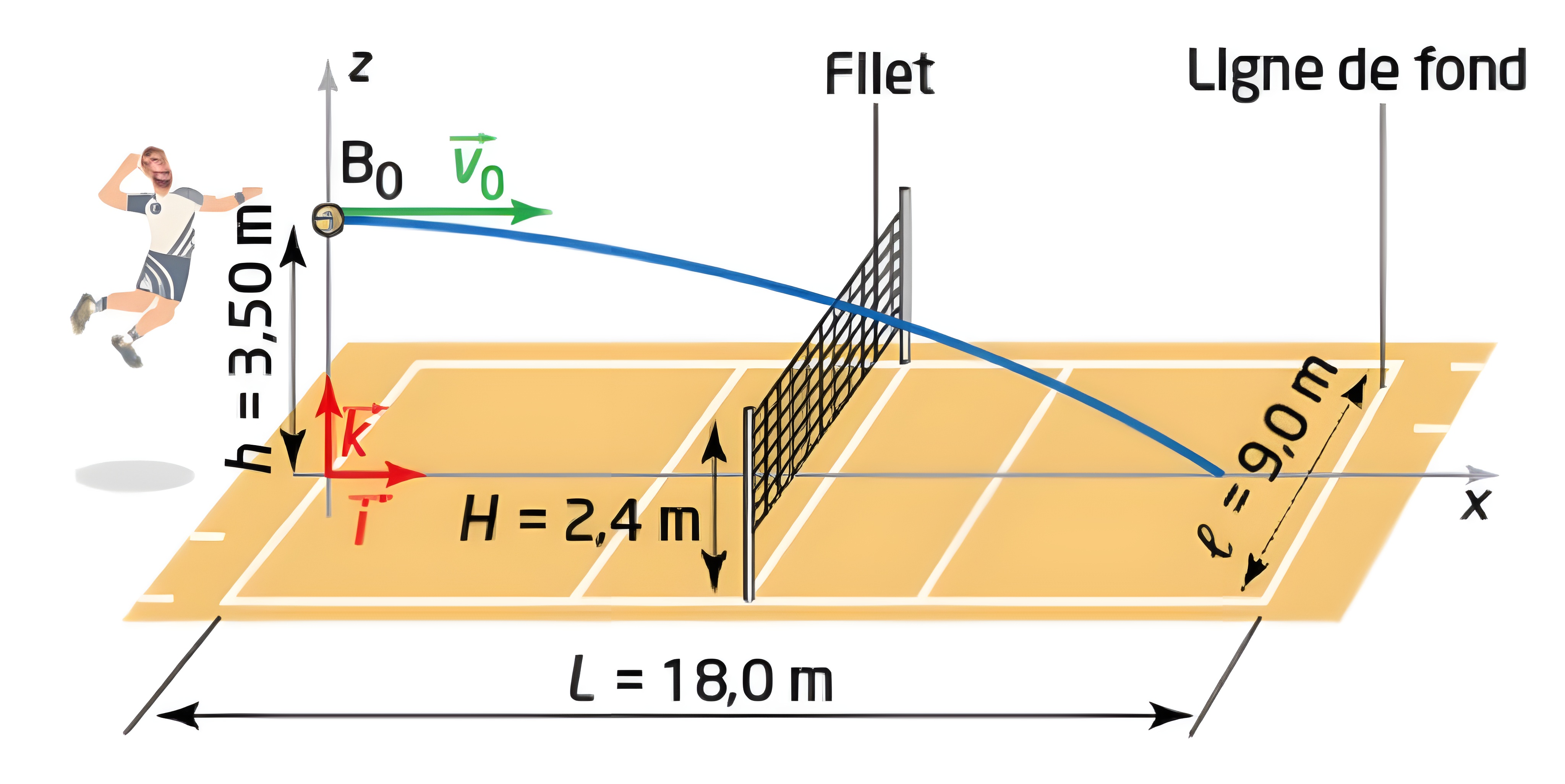
rayon de la balle : $r=\pu{10 cm}$

Aspects énergétiques

Lors d’une chute libre,
l’énergie mécanique $E_m$ du système est la somme
de son énergie cinétique $E_c=\frac12 mv^2$ et de son
énergie potentielle de pesanteur $E_{pp}=mgz$.

Et comme la seule force agissant sur le système est conservative, le théorème de l’énergie mécanique,

$$\Delta E_m = \sum W_\mathrm{AB}(\vec{F}_\mathrm{n.c.}) = 0$$

nous assure que l'énergie mécanique
est conservée pendant le mouvement.

L’énergie cinétique est ainsi convertie en énergie potentielle de pesanteur et inversement.

Champ électrique créé par
un condensateur plan

Un condensateur plan est constitué de deux plaques métalliques chargées, parallèles entre elles
et séparées par un isolant (air, huile…).

Il se crée alors un champ électrique uniforme dans
la zone de l'espace située entre les deux plaques (suffisamment loin des bords).

Les lignes de champ sont perpendiculaires aux plaques, orientées de la plaque chargée positivement vers la plaque chargée négativement.

La norme $E$ du champ créé par le condensateur plan est donnée par la formule :

$$E=\frac U d$$

$U$ est la tension entre les plaques (en $\pu{V}$)
$d$ est la tension entre els plaques (en $\pu{m}$)
$E$ (en $\pu{V*m-1}$)

Mouvement dans un
champ électrique uniforme

Prenons l’exemple du principe de fonctionnement
des imprimantes à jet d’encre continu dévié, principalement utilisées pour imprimer les dates d’expiration figurant sur les produits alimentaires.

Le jet d’encre sort de la tête d’impression par une buse qui le décompose en très petites gouttes dont certaines sont chargées électriquement.

Celles-ci passent sous un déflecteur constitué de deux plaques P₁ et P₂ parallèles, chargées électriquement, assimilables à un condensateur plan. Ces plaques dévient les gouttes chargées de leur trajectoire initiale.

Les gouttes non chargées poursuivent leur mouvement rectiligne vers une gouttière de recyclage.

À la date $t_0=0$ s, la goutte d’encre G pénètre dans
la zone de champ électrique uniforme au niveau du
point O avec une vitesse initiale notée $\vec{v}_0=v_0\,\vec{i}$.

Sachant que la goutte, chargée négativement,
est déviée vers le haut, quel est le signe des
charges portées par P₁ et P₁ ?

Que peut-on dire du champ $\vec{E}$ entre les plaques ?

Obtenons les équations horaires du mouvement
de la goutte dans le déflecteur.

On se place dans le référentiel terrestre supposé galiléen et muni du repère d'espace $(O;\vec{i},\vec{j},\vec{k})$.

Bilan des forces extérieures s’appliquant à la goutte :

poids $\vec{P}=m\vec{g}$
force électrique $\vec{F}_e = $ $q\vec{E}$
actions de l'air sur la bille
(force d'Archimède, frottements)

Dans la suite, on négligera les autres
forces que la force électrique.

Vecteur accélération

Application de la deuxième loi de Newton :

$$m{\color{#61D836}\vec{a}} = \sum \color{#FF968D}\vec{F}_\mathrm{ext}$$

$$\Rightarrow m{\color{#61D836}\vec{a}}={\color{#FF968D}q\vec{E}} \Rightarrow {\color{#61D836}\vec{a}}=\frac {\color{#FF968D}q} m {\color{#FF968D}\vec{E}}$$

Comme $q<0$, le mouvement est
uniformément accéléré vers le haut.

Coordonnées du vecteur accélération :

$$ \vec{a}(t)= \begin{cases} a_x(t)=0\\ a_y(t)=0\\ a_z(t)=-\frac {qE}{m} \end{cases} $$

Rq : en effet, $\vec{E}=-E\,\vec{k}$

Vecteur vitesse

On primitive les coordonnées de $\vec{a}$.

$\Rightarrow$ $ \vec{v}(t)= \begin{cases} v_x(t)=c_1\\ v_y(t)=c_2\\ v_z(t)=-\frac{qE}{m} t+c_3 \end{cases} $

D’après les conditions initiales :

$v_x(0)=c_1=v_0$
$v_y(0)=c_2=0$
$v_z(0)=c_3=0$

D’où

$$ \vec{v}(t)= \begin{cases} v_x(t)=v_0\\ v_y(t)=0\\ v_z(t)=-\frac{qE}{m} t \end{cases} $$

Coordonnées du vecteur position
= équations horaires du mouvement

On primitive les coordonnées de $\vec{v}$.

$\Rightarrow$ $ \overrightarrow{OG}(t)= \begin{cases} x_\mathrm{G}(t)=v_0 t + c'_1\\ y_\mathrm{G}(t)=c'_2\\ z_\mathrm{G}(t)=-\frac{qE}{2m} t^2+c'_3 \end{cases} $

D’après les conditions initiales :

$x_\mathrm{G}(0)=c'_1=0$
$y_\mathrm{G}(0)=c'_2=0$
$z_\mathrm{G}(0)=c'_3=0$

D’où

$ \overrightarrow{OG}(t)= \begin{cases} x_\mathrm{G}(t)=v_0 t\\ y_\mathrm{G}(t)=0\\ z_\mathrm{G}(t)=-\frac{qE}{2m} t^2 \end{cases} $

Déterminer la valeur de la hauteur H’I du point d’impact I de la goutte sur le support d’impression
si on suppose que le mouvement de la goutte est rectiligne uniforme en sortie du déflecteur (de S à I).

Marche à suivre possible :

Déterminer le temps $t_S$ auquel la goutte sort du déflecteur et la déviation HS.
Déterminer les coordonnées de $\vec{v}_S$.
Montrer que $\tan\alpha=-\frac{qEL}{mv_0^2}$

Rq : on va voir dans la fin du cours comment on aurait pu obtenir cette dernière relation à partir de la conservation de l'énergie mécanique de la goutte.

Données pour l’application numérique :

$m=\pu{2e-10 kg}$
$q=\pu{-4e-13 C}$
$L=\pu{2 cm}$
$D=\pu{3 cm}$
$E=\pu{9e5 V*m-1}$
$v_0=\pu{20e5 m*s-1}$

Aspect énergétique

On retrouve une utilisation du champ électrique uniforme d’un condensateur dans les
accélérateurs linéaires de particules chargées.

Comme leur nom l'indique, leur but est d'accélérer fortement une particule chargée (électron ou ion).

Cette particule peut ensuite servir à une expérience
de physique des particules ou en radiothérapie. Et en l'envoyant sur une cible, on crée des rayons X utilisée en imagerie médicale ou, là encore, en radiothérapie.

Imaginons qu’un électron est injecté
sans vitesse initiale en A.

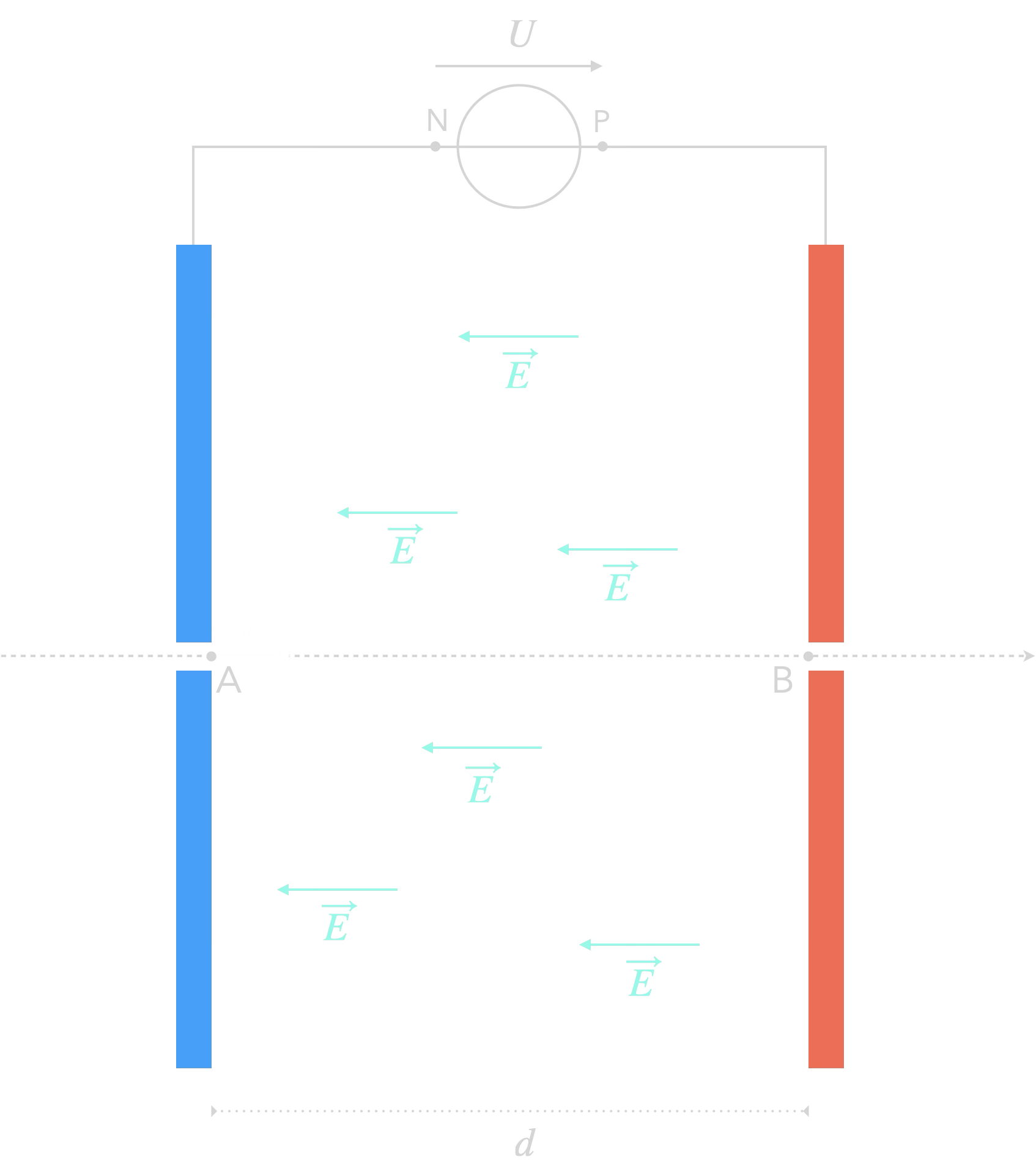
Si on néglige l’action de la gravité, le théorème
de l’énergie cinétique nous dit que :

$$ \begin{aligned} \Delta E_c &= \sum W_\mathrm{AB}(\vec{F}_\mathrm{ext})\\ &=\overrightarrow{\mathrm{AB}}\cdot \overrightarrow{F_e}\\ &=-qEd \end{aligned} $$

Or $E=\frac Ud$. On obtient donc :

$$E_{c\mathrm{B}}-E_{c\mathrm{A}}=-qU$$

Et comme par hypothèse, $v_A = 0$

$v_B=$ $\displaystyle\sqrt{\frac{2qU}{m}}$

Pour une tension de $\pu{20,0 kV}$,
on obtient une vitesse de :

$$ \begin{aligned} v_B &= \sqrt{\frac{2\times (\pu{1,60E-19 C})\times(\pu{20,0E3 V})}{\pu{9,11E-31 kg}}}\\ &= \pu{8,38E7 m*s-1} \end{aligned} $$

Retour site