Cinétique d’une transformation chimique
Une transformation chimique
peut se dérouler plus ou moins vite.
Transformation lente ou rapide
Pour étudier la cinétique d’une transformation,
on utilise un capteur de suivi temporel
de l’évolution
d’un système.
Rq : ce capteur peut être simplement l'œil.
Si le temps de réponse du capteur est trop grand
ou si les manipulations à réaliser avant le début
des mesures empêchent la mise en œuvre du suivi cinétique, la transformation est dite rapide.
Sinon, elle est dite lente.
Vitesse volumique d’apparition
Dans un réacteur de volume constant,
la vitesse volumique d’apparition (ou de formation) d’une espèce à une date $t$ est égale à la valeur
de la dérivée temporelle de sa concentration
en quantité de matière à cette date.
Exemple :
La vitesse d'apparition du diiode s’écrit :
$\displaystyle v_{{\color{#FF968D}a},\ce{I2}}{\color{#FFF056}(t)}=\frac{\mathrm{d}\left[\ce{I_2}{\color{#FFF056}(t)}\right]}{\mathrm{d}t}$
Si l’espèce est produite au cours de la transformation, sa concentration augmente et donc
sa vitesse d’apparition est positive.
Si l’espèce est consommée (réactif),
sa vitesse d'apparition est négative.
Graphiquement, la valeur de la vitesse d’apparition
à un instant $t$ est donnée par la valeur de la pente de
la tangente à la courbe représentant l’évolution
de la concentration à cette date.
Que vaut la vitesse de formation à $t=2$ min ?
Et à $t=3$ min ?
Et la vitesse d’apparition initiale ($t=0$ s) ?
Vitesse volumique de disparition
La vitesse volumique de disparition d’une espèce est l’opposé de sa vitesse volumique d’apparition :
$$v_{{\color{#56C1FF}d},\mathrm{X}}{\color{#FFF056}(t)} = -v_{{\color{#FF968D}a},\mathrm{X}}{\color{#FFF056}(t)}$$
Dans un réacteur de volume constant,
la vitesse volumique de disparition d’une espèce
à une date $t$ est donc égale à l’opposé de la
dérivée temporelle de sa concentration
en quantité de matière à cette date.
Exemple :
La vitesse de disparition
du peroxyde d’hydrogène s’écrit :
$\displaystyle v_{{\color{#56C1FF}d},\ce{H2O2}}{\color{#FFF056}(t)}={\color{#56C1FF}-}\frac{\mathrm{d}\left[\ce{H2O2}{\color{#FFF056}(t)}\right]}{\mathrm{d}t}$
Et graphiquement ?
Que vaut la vitesse de disparition du réactif à $t=30$ s ?
Rq:
Les vitesses volumiques présentent l’avantage
de ne pas dépendre du volume du système.
Loi de vitesse et facteurs cinétiques
Une loi de vitesse est l’expression de la vitesse volumique d’apparition ou de disparition d’une espèce en fonction des différents paramètres qui la modifient.
qui apparaissent dans la loi de vitesse
(température, concentration).
Ce sont sont donc les paramètres
qui influent sur la durée d’une transformation.
Exemple :
La loi de vitesse de disparition de l’ester éthanoate d’éthyle par hydrolyse basique est de la forme :
$$v=k({\color{#FFF056}T})\ce{{\color{#56C1FF}[ester][HO-]}}$$
où $k(T)$, appelée constante de vitesse, rend compte
de l’influence de la température sur cette réaction.
Loi de vitesse d’ordre 1
Une réaction est dite d’ordre 1 si sa loi de vitesse
de disparition d’une espèce se met sous la forme
où $\ce{A}$ représente un réactif de la réaction.
Comme $v_d=-\frac{\mathrm{d}\ce{[A]}}{\mathrm{d} t}$, on a :
$$-\frac{\mathrm{d}\ce{[A]}}{\mathrm{d} t} = k\ce{[A]}$$
$$\color{#FF968D}\frac{\mathrm{d}\ce{[A]}}{\mathrm{d} t} + k\ce{[A]} = 0$$
On obtient donc une équation différentielle
du premier ordre (à coefficients constants).
Une équation différentielle est une équation
où les inconnues sont des fonctions et qui
lie une fonction et ses dérivées.
Une équation différentielle du premier ordre fait intervenir une fonction et sa dérivée première.
La solution d’une telle équation différentielle
est de la forme :
$$\color{#FF968D}\ce{[A]}(t)= C\times\mathrm{e}^{-kt}$$
où $C$ est une constante.
$\mathrm{e}^x = \exp(x)$ est la fonction exponentielle.
$\ln\left(\mathrm{e}^x\right)=x$
On détermine $C$ grâce aux conditions initiales :
$\ce{[A]}(t=0)=C\times\mathrm{e}^{-k\times 0} = \color{#FFF056}C = \ce{[A]}_0$
D'où
$$\color{#FF968D}\ce{[A]}(t)= \ce{[A]}_0\times\mathrm{e}^{-kt}$$
L’évolution de la concentration dépend donc de la
concentration initiale $[\mathrm{A_0}]$ et de la température
(via la constante de vitesse $k({\color{#FFF056}T})$).
En prenant le logarithme de $ [\mathrm{A}](t) $,
on peut vérifier que cette loi est d’ordre 1 :
$\ln\left(\ce{[A]}(t)\right) = \ln(\ce{[A]}_0) -k\times t$
On obtient une fonction affine décroissante du temps.
Donc si $\ln\left(\ce{[A]}(t)\right)$ est modélisable par une
fonction affine, la loi de vitesse est d'ordre 1 !
Catalyse et catalyseur
les caractéristiques thermodynamiques.
Étant à la fois réactif et produit,
il n’apparaît pas dans l’équation de la réaction
qui modélise la transformation.
Selon les états physiques du catalyseur et du milieu réactionnel, la catalyse est qualifiée
d’homogène ou d’hétérogène.
Exemples :
Le platine catalyse la dismutation du peroxyde d’hydrogène (catalyse hétérogène).
Les enzymes sont des catalyseurs biologiques particulièrement efficaces (catalyse homogène).
Temps de demi-réaction
a atteint la moitié de sa valeur finale.
Si $\ce{R}$ est le réactif limitant d’une transformation :
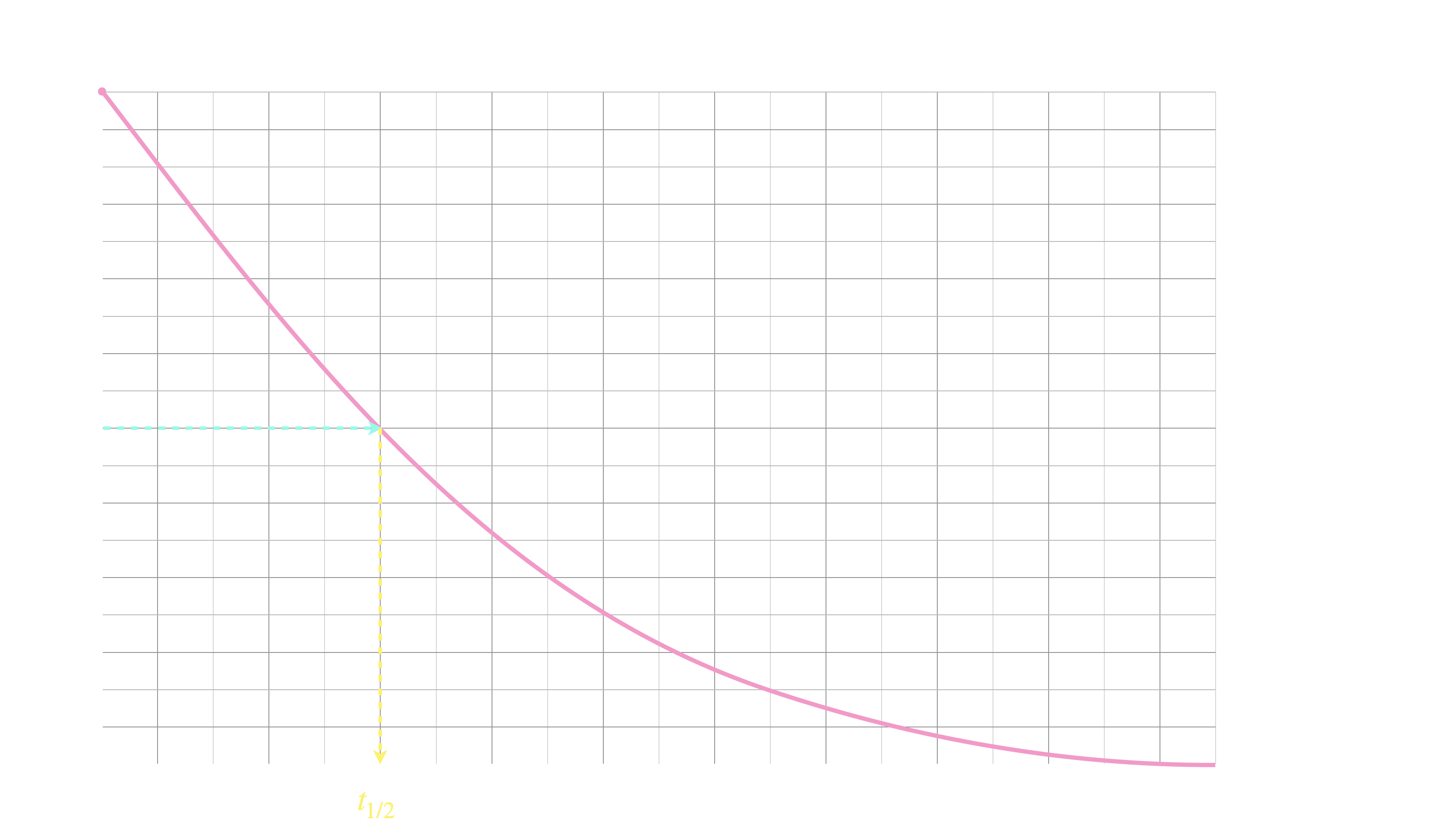
$t_{1/2}$ est alors la durée au bout de laquelle la concentration initiale est divisée par deux.
En effet, si $\ce{R}$ est entièrement consommée
à l'avancement final, alors il sera à moitié consommé
à la moitié de l'avancement final (quelle que soit
sa stœchiométrie dans la réaction).
Et la concentration sera donc bien divisée par deux.
Et pour un produit :
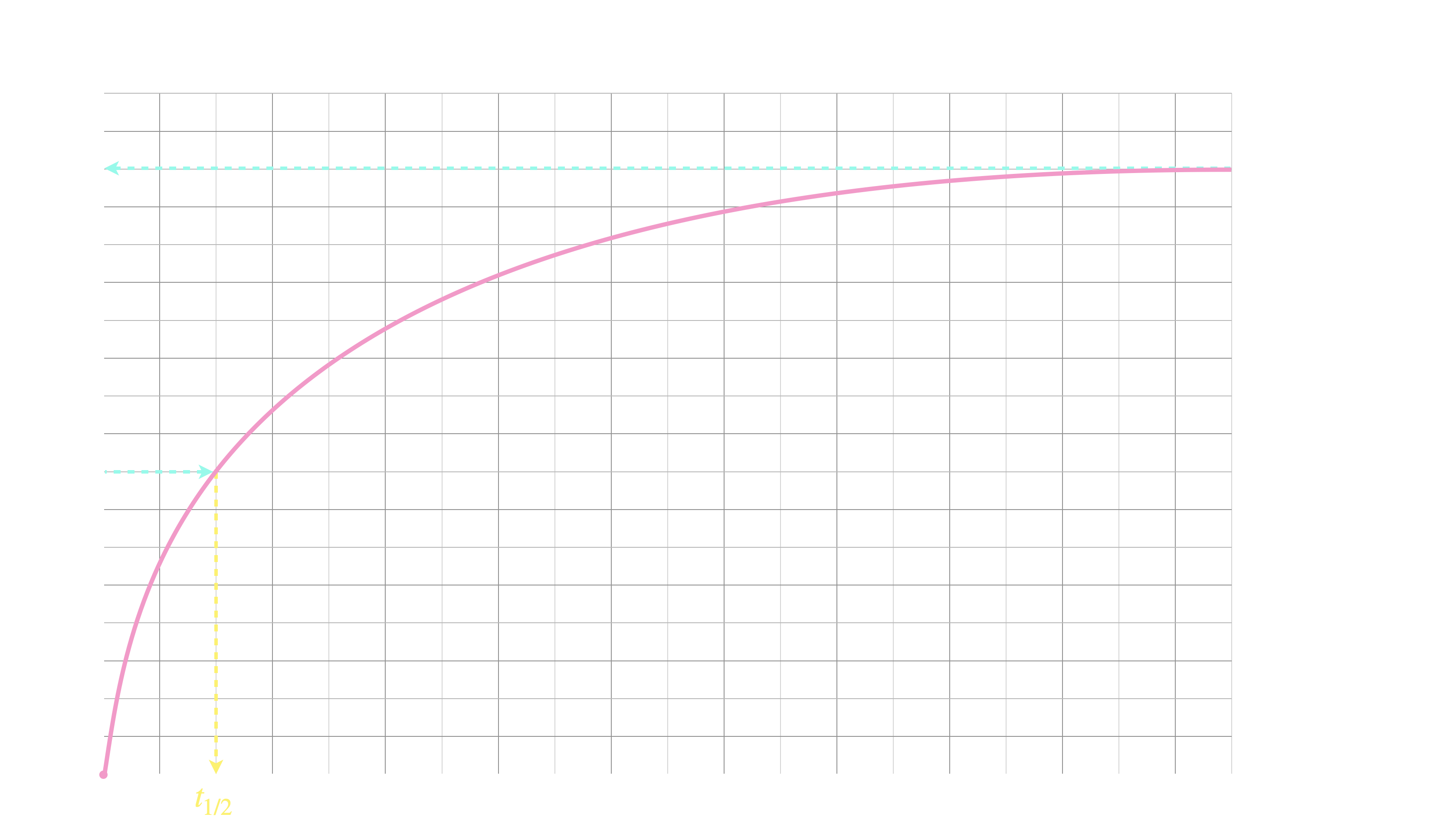
Si la concentration initiale est nulle, $t_{1/2}$ est la durée au bout de laquelle la concentration atteint la moitié
de sa valeur limite finale $\mathrm{[P]}_f$.
Rq :
- ⚠️ Le temps de demi-réaction ne correspond pas
à la moitié de la durée de réaction ! - Le temps de demi-réaction permet d'évaluer la durée de la transformation chimique (quelques $t_{1/2}$)
et donc de comparer entre elles la rapidité
des transformations.
Modélisation microscopique
On modélise une transformation chimique à l’échelle microscopique par un mécanisme réactionnel qui propose un ensemble d’actes élémentaires a priori réalisés lors de la conversion des entités des réactifs en entités des produits, passant éventuellement par une ou plusieurs entités d’intermédiaires réactionnels.
Le mécanisme doit être cohérent avec la stœchiométrie de la réaction, la loi de vitesse et toute autre donnée expérimentale obtenue à l’échelle macroscopique.
L’acte élémentaire (ou étape élémentaire) correspond à un modèle, au niveau moléculaire, de conversion d’entités se déroulant en une seule étape.
Un intermédiaire réactionnel est une entité intervenant dans un mécanisme réactionnel, formée directement ou indirectement à partir des réactifs,
et convertie directement ou indirectement
en produits de la réaction.
En d'autres mots, il est formé, puis il est utilisé.
Exemple :
Le mécanisme réactionnel de la réaction
$\ce{(H_3C)3C-Cℓ + HO- -> (H_3C)3C-OH + Cℓ^-}$
se décompose en deux actes élémentaires.
- $\ce{(H_3C)3C-Cℓ \leftrightarrows {\color{#56C1FF}(H_3C)_3C^+} + Cℓ^-}$
- $\ce{ {\color{#56C1FF}(H_3C)_3C^+} + HO- \leftrightarrows (H_3C)3C-OH}$
$\ce{\color{#56C1FF}(H_3C)_3C^+}$ est ici un intermédiaire réactionnel.
On représente les modifications des structures électroniques des entités au cours d’un acte élémentaire à l’aide du formalisme de la flèche courbe.
Une flèche courbe symbolise le mouvement
d’un doublet d’électrons d’un
site donneur
vers un site accepteur.
Un site donneur peut être :
- un doublet non liant
- un doublet liant
(d'une liaison multiple ou simple) - un atome portant une charge négative
ou fortement polarisé négativement
Un site accepteur peut être :
- un atome possédant une lacune électronique
- un atome portant une charge positive
ou polarisé positivement
Pour représenter ces mouvements de doublets,
il faut partir des schémas de Lewis des entités.
Prenons l’exemple du 2e acte élémentaire
de l’exemple précédent :
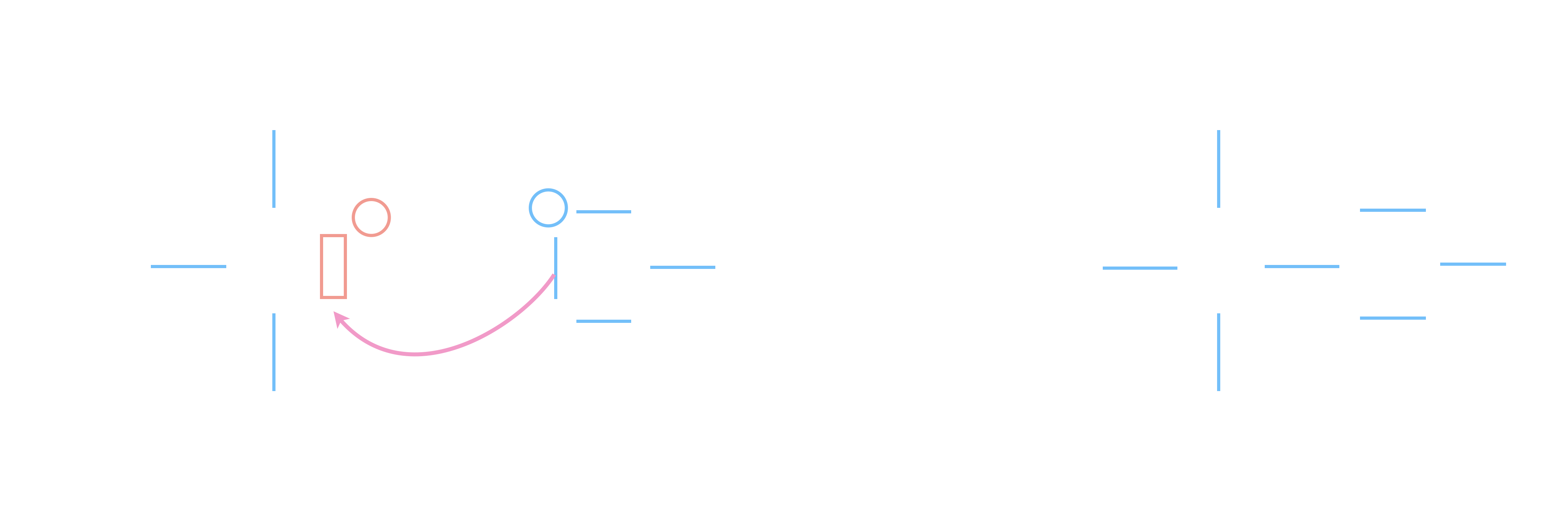
Un catalyseur modifie le mécanisme réactionnel.
La transformation modélisée par la réaction
$\ce{H2C-Cℓ + HO- -> H3C-OH + Cℓ^-}$
se déroule en un seul acte élémentaire.
Mais en présence d’ions iodures ${\color{#FFF056}\ce{I-}}$,
le mécanisme est modifié :
- $\ce{ {\color{#73FDEA}\ce{H_3C-Cℓ}} + {\color{#FFF056}\ce{I-}}\leftrightarrows {\color{#56C1FF}\ce{H_3C-I}} + {\color{#FF95CA}\ce{Cℓ^-}}}$
- $\ce{ {\color{#56C1FF}\ce{H_3C-I}} + {\color{#73FDEA}\ce{HO-}} \leftrightarrows {\color{#FF95CA}\ce{H_3C-OH}} + {\color{#FFF056}\ce{I-}}}$
Le ${\color{#FFF056}\ce{I-}}$ est momentanément utilisé puis finit par être reformé et donc n'apparaît pas dans l'équation bilan.
Différence entre catalyseur
et intermédiaire réactionnel ?
L'intermédiaire réactionnel apparaît d'abord comme produit d'un acte élémentaire puis comme réactif d'un autre acte élémentaire alors que pour le catalyseur, c'est l'inverse, il apparaît d'abord comme réactif d'un acte élémentaire puis comme produit d'un autre.
Par conséquent, le catalyseur n’est pas nécessaire
à la réaction alors que l’intermédiaire réactionnel
est une étape obligée.
Interprétation microscopique
des facteurs cinétiques
Pour qu’un acte élémentaire ait lieu,
il faut un choc entre les entités.
Or plus la concentration est grande,
plus la probabilité de chocs est grande.
Et plus la température est grande,
plus les entités vont vite et donc
plus la fréquence des chocs
et leur énergie sont élevées.
Cela explique pourquoi la concentration et la température sont des facteurs cinétiques.