Diffraction et interférences

Signature du caractère ondulatoire

Quels indices expérimentaux témoignent-ils
de la nature ondulatoire d’un phénomène ?

  • la diffraction
  • les interférences

Animations interactives

Diffraction

La diffraction d’une onde correspond à l’étalement
des directions de propagation lorsque l’onde rencontre un obstacle ou une ouverture.

L'étalement est d'autant plus marqué que
l'obstacle ou l'ouverture sont petits.

La fréquence $f$ et la célérité $c$ de l'onde, et donc
sa longueur d'onde $\lambda=c/f$ sont conservées.

Le phénomène de diffraction est nettement observé lorsque la taille caractéristique $a$ de l’obstacle ou ouverture est du même ordre de grandeur que la longueur d’onde $\lambda$ de l’onde.

Dans le cas d'ondes lumineuse, le critère est moins restrictif et le phénomène est encore apparent pour
des tailles $a$ jusqu'à 100 fois plus grandes que $\lambda$.

La diffraction est caractérisée par
un angle de diffraction défini comme
l’angle entre la direction de propagation
sans diffraction et la direction définie
par le milieu de la “première extinction”.

Dans le cas de la diffraction d’une onde lumineuse monochromatique de longueur d’onde $\lambda$ (produite par un laser) par une fente rectangulaire de largeur $a$, l’angle caractéristique de diffraction $\theta$ est donné par :


$$\theta\approx\frac{\lambda}{a}$$
  • $\lambda$ en $\pu{m}$
  • $a$ en $\pu{m}$
  • $\theta$ en $\pu{rad}$
  • Pour une longueur d'onde fixée :
    $a \searrow\;\; \Rightarrow \;\;$$\theta$ $\nearrow$

  • Pour une taille $a$ fixée :
    $\lambda \nearrow\;\; \Rightarrow \;\;$$\theta$ $\nearrow$

Dans l’approximation des petits angles ($\theta\ll 1$), exprimer la taille de la tâche centrale $L$
en fonction de $\lambda$, $D$ et $a$.

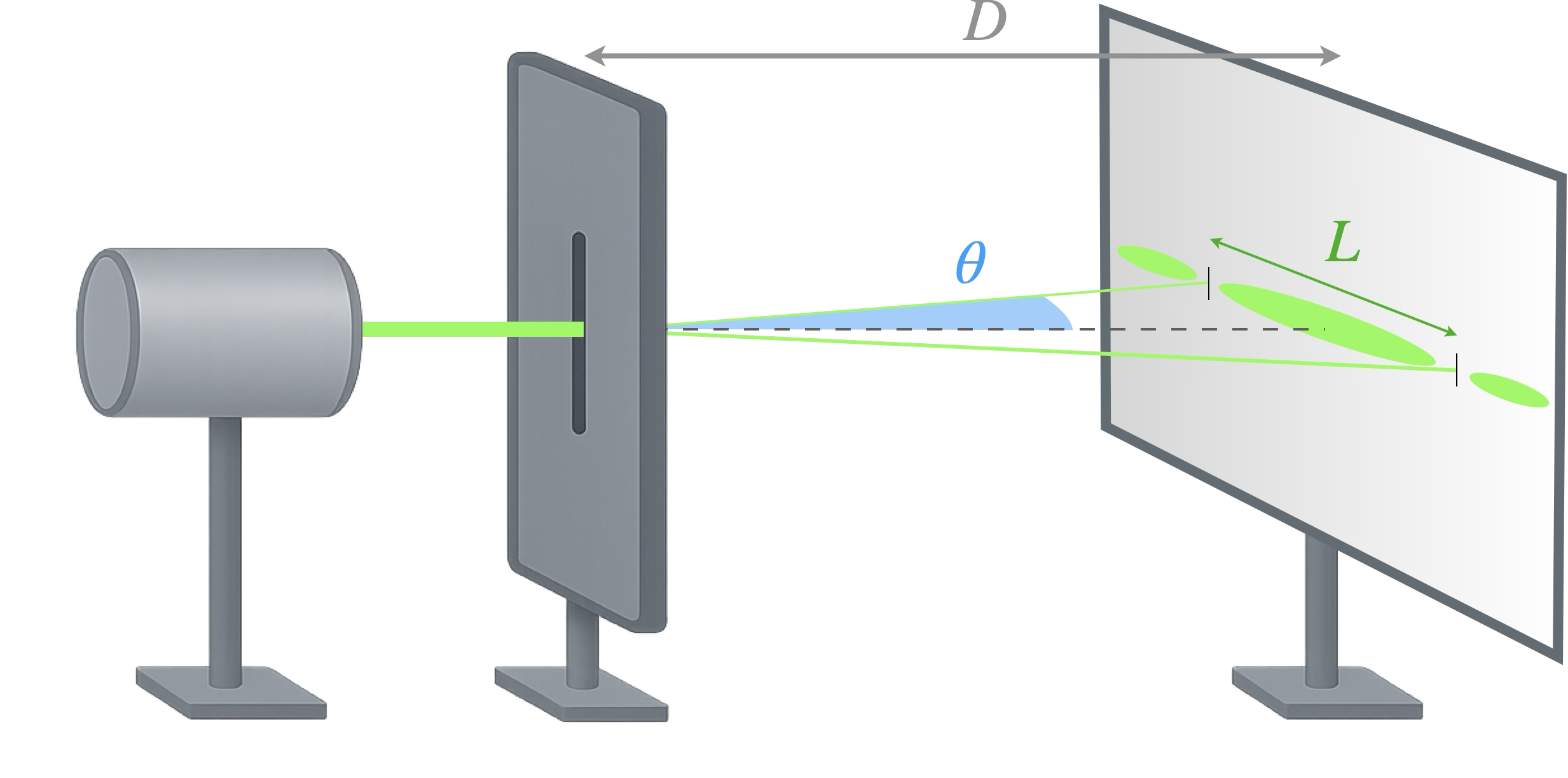
$$L\approx \frac{2\lambda D}{a}$$

Démonstration :

$$\tan\theta = \frac{L/2}{D}$$

Or d'après l'approximation des petits angles :
$\tan\theta \approx \theta$ (⚠️ valable qu'en radians)

D'où :

$$\theta\approx \frac{L}{2D}$$

Et comme $\theta=\frac{\lambda}{a}$, on obtient finalement :

$$\displaystyle\frac\lambda a \approx \frac{L}{2D}$$

$\displaystyle\Rightarrow L \approx \frac{2D\lambda}{a}$

Exemples de conséquences concrètes :

l'onde diffractée peut atteindre des endroits qui
seraient inaccessibles sans l'étalement
des directions de propagation.

Un son diffracté par l'entrebâillement d'une porte peut ainsi être entendu dans toute la pièce et un bateau
peut subir la houle même à l'abri d'une digue.

La figure de diffraction nous renseigne sur la forme géométrique de l’obstacle qu’a rencontré l’onde !

Un grand nombre de structures de protéines ont ainsi été déterminées par diffraction (on cristallise d’abord la protéine puis on envoie le rayonnement dans le cristal)

Quel doit être l’ordre de grandeur
de la longueur d’onde à utiliser ?

À quelle partie du spectre électromagnétique appartient le rayonnement ?

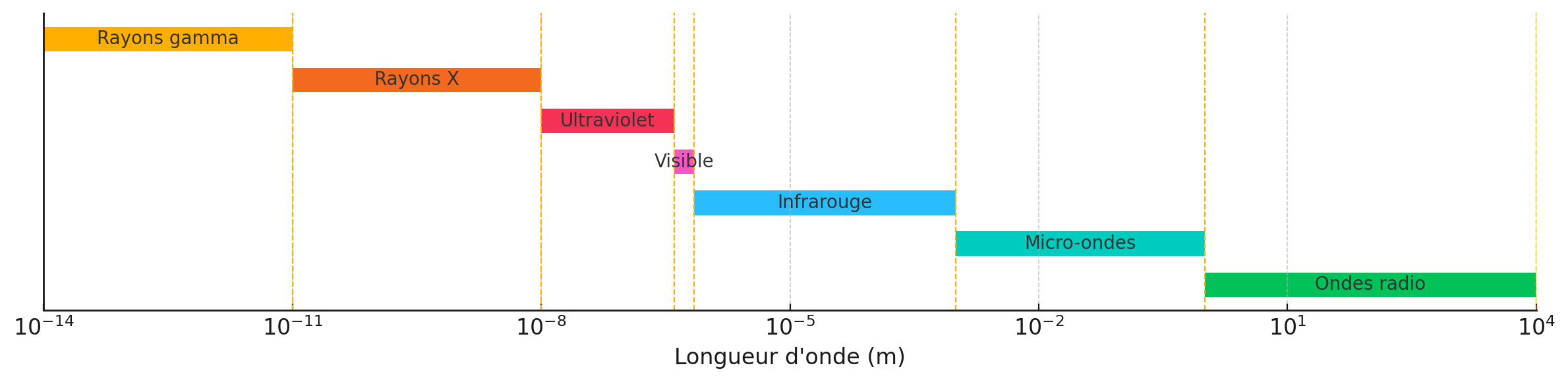
C’est aussi une diffraction aux rayons X qui a
permis de découvrir (grâce à Rosalind Franklin)
la structure en double hélice de l’ADN.

Enfin, la tâche de diffraction correspondant à l’ouverture d’un télescope ou d’une lunette donne
la résolution ultime atteignable par l’appareil.

Moins fondamental mais intéressant :

la forme des miroirs et des tiges tenant le miroir secondaire expliquent les aigrette sur les images d'étoile prises par Hubble ou Webb.

Comparaison Hubble/Webb

Interférences de deux ondes

Lorsque deux ondes se rencontrent en un point,
leurs amplitudes en ce point s’additionnent.

Il n'y a pas d'interaction, chaque onde évoluant indépendamment l'une de l'autre, mais il y a superposition des perturbations.

Conditions d’observation :


  • les ondes doivent être de même nature ;
  • les sources doivent être synchrones
    = de même fréquence ;
  • les sources doivent être cohérentes
    = le retard du signal émis par l'une
    par rapport à l'autre reste constant
    (= déphasage constant)

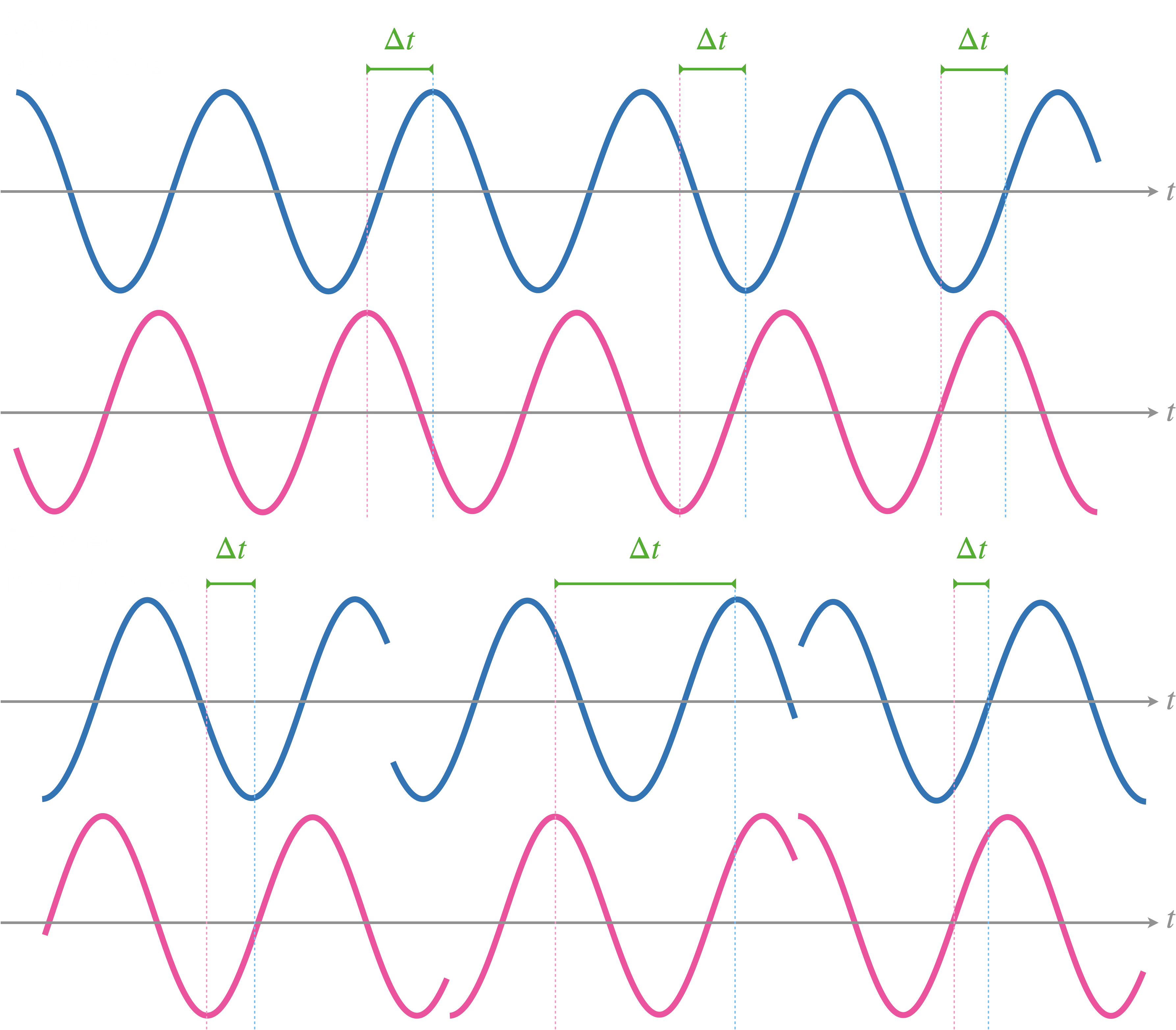
Deux signaux sont dit en phase s’ils coïncident
(les extrema se correspondent).

Si en un point, les signaux des deux ondes sont en phase, on dit que l'interférence est constructive.

Deux signaux sont dit en opposition de phase
si les maxima de l’un correspondent aux minima
de l’autre (il y a un déphasage de π ou 180°).

Si en un point, les signaux des deux ondes sont
en opposition de phase, on dit que
l'interférence est destructive.

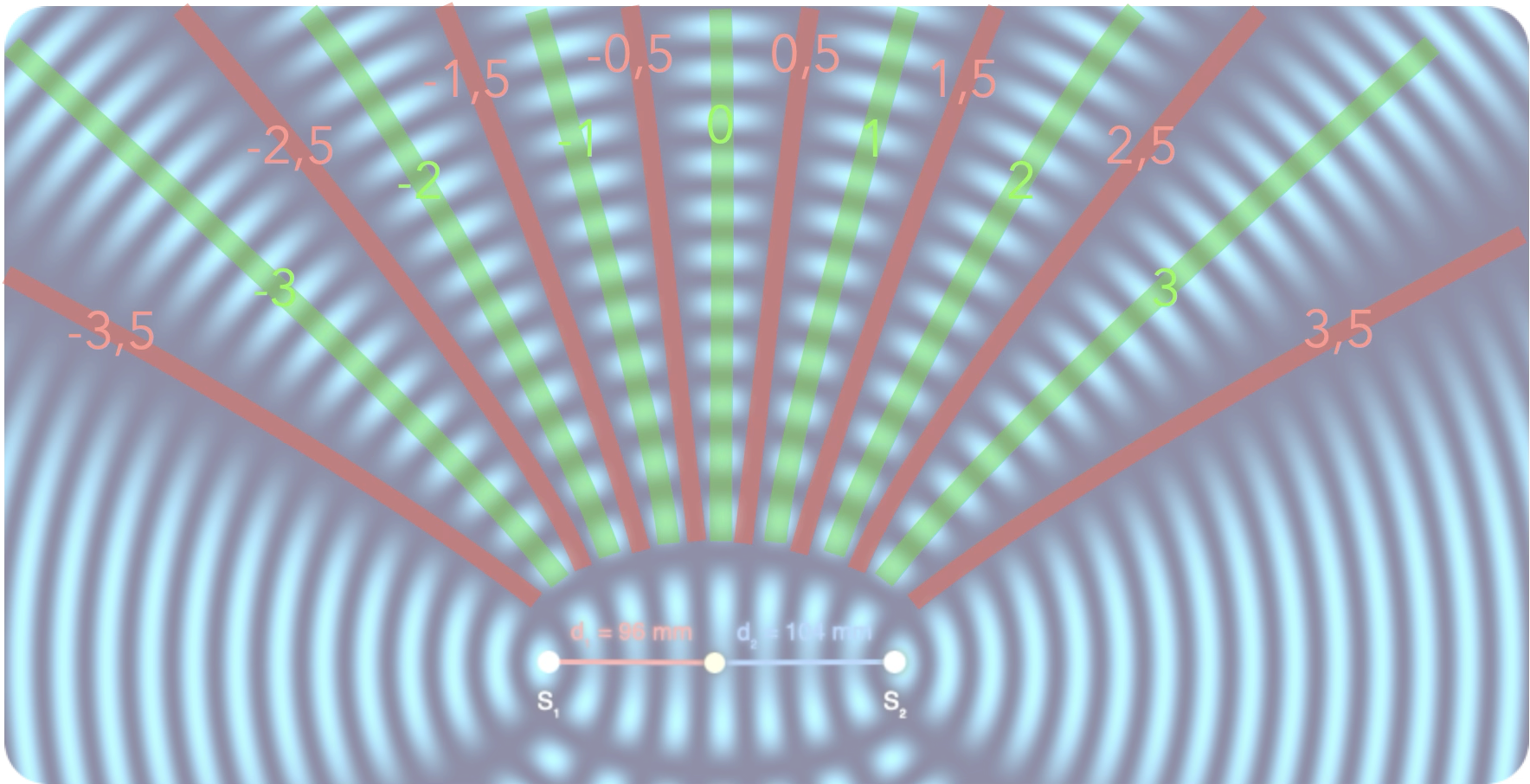
Supposons que les oscillations
des sources S1 et S2 soient en phase.

La condition pour observer une interférence constructive en M est que la différence entre
les distances parcourues sur chacun des chemins
(${\color{#61D836}\delta}=\mathrm{{\color{#FF968D}S_2M}-{\color{#56C1FF}S_1M}} $) induise un déphasage
valant un multiple de 2π.

$\displaystyle2\pi\times \frac{\delta}{\lambda}= k\times 2\pi\;,\; k\in\mathbb{Z}$

On en déduit la condition pour obtenir
en un point une interférence constructive :


$$\frac{\delta}{\lambda} = k \;,\; k\in\mathbb{Z}$$

Autrement dit, la distance supplémentaire parcourue sur le chemin le plus long doit être un multiple
de la longueur d'onde.

Et pour des interférences destructives, il faut :

$$ \begin{aligned} 2\pi\frac{\delta}{\lambda}&=\pi + k\times 2\pi\\ &=2\pi\times\left(k+\frac{1}{2}\right) \end{aligned} $$

$$ \frac{\delta}{\lambda} = \left(k+\frac12\right) \;,\; k\in \mathbb{Z}$$

La distance supplémentaire doit valoir
un nombre impair de demi-longueurs d'onde.

L’entier $k$ est appelé ordre d’interférence.

Dans le cas de l’expérience optique des trous d’Young (ou des fentes d’Young), les deux trous éclairés par
la source lumineuse agissent ensuite comme
deux sources synchrones et cohérentes
séparées d’une distance $a$.

On doit maintenant prendre en compte l’éventuel ralentissement de la lumière dans un milieu d’indice optique $n$, la différence de distance $\mathrm{S_2M-S_1M}$ prend alors le nom de différence de chemin optique
$\mathrm{[S_2M]-[S_1M]}=n\times(\mathrm{S_2M-S_1M})$.

Si la distance $D$ entre les trous et l’écran est
telle que $D\gg a$, alors la différence de chemin optique en un point de l’écran d’abscisse $x$ est approximée par :

$$\delta=\frac{nax}{D}$$

En déduire l'abscisse $x_k$ sur l'écran
où apparaît la $k$e frange brillante.

D'après la condition d'interférence constructive :

$$ \delta = k\lambda\quad \text{avec } k\in\mathbb{Z} $$

$$ \Rightarrow x_k=\frac{k\lambda D}{na} $$

Et pour les franges sombres ?

$$ x'_k=\frac{(k+\frac12)\lambda D}{na} $$

L'interfrange $i$ sur l'écran est définie comme
la distance entre le centre de deux franges brillantes (ou de deux franges sombres) consécutives.

Établir l'expression de l'interfrange $i$.

$$ \begin{aligned} i &= x_{k+1}-x_k\\ &=\frac{(k+1)\lambda D}{na}-\frac{k\lambda D}{na}\\ &=\frac{\lambda D}{na} \end{aligned} $$
  • Si $\lambda\nearrow$, $i$ $\nearrow$
  • Si $a\nearrow$, $i$ $\searrow$
  • Si $D\nearrow$, $i$ $\nearrow$
  • $i$ est indépendante de
    l'ordre d'interférence $k$

Conséquences pratiques :

  • casques/écouteurs à réduction de bruit active
  • couleurs interférentielles
  • interférométrie

Utilisée en astronomie, métrologie,
océanographie, séismologie, etc.
cf. exercice "interférométrie et volcan"

Et dans de nombreuses expériences scientifiques (comme celle de Michelson et Morley
à la fin du 19e siècle)

Grâce à l’interférométrie, un réseau de télescopes ou radiotélescopes atteint une résolution équivalente
à celle d’un miroir (ou radiotélescope) de diamètre équivalent à l’écart entre les instruments combinés.

Pour aller plus loin sur les télescopes

La détection des ondes gravitationnelles
utilise aussi l’interférométrie.

cf. exercice “interféromètre gravitationnel”

La première détection a tout juste 10 ans.
et elle s'est faite grâce à un interféromètre
ayant des bras de 4 km de long !

Enfin, si on décale légèrement la fréquence des sources, on observe non plus seulement des franges dans l’espace mais aussi dans le temps.

On les appelle battements. On les utilise par
exemple pour accorder les instruments.

Retour site