Modéliser l’écoulement
d’un fluide

Fluide incompressible

Un fluide est un liquide ou un gaz.

Un fluide incompressible est un fluide
dont la masse volumique est constante.

$$\rho=\mathrm{cste}$$

Le modèle nécessite une température
constante et homogène dans le fluide.

Et les vitesses d'écoulement doivent être petites devant la célérité des ondes acoustiques dans le fluide
($v\ll c_\mathrm{son}$).

Poussée d’Archimède

Un corps plongé dans un fluide incompressible au repos reçoit une force opposée au poids du liquide déplacée.

C'est la poussée d'Archimède notée $\vec{\pi}_A$.

Cette action est la résultante des forces
de pression du fluide sur le corps.

La résultante est non nulle du fait de la présence d'une gravité qui rend la pression plus grande en profondeur.

Calculons la résultante des forces de pression sur un cylindre vertical de hauteur $h$ et section $S$ immergé dans une fluide incompressible au repos
de masse volumique $\rho$.

Les forces pressantes sur la face latérale s’annulent deux à deux à une altitude donnée.

Il ne reste plus qu'à considérer
les deux faces horizontales...

Sur la face du bas : $\vec{F}_{pb} = P(z_0)\times S\times \vec{k}$

Sur la face du haut : $\vec{F}_{ph}=-P(z_0+h) \times S\times \vec{k}$

Or d’après le principe fondamental de l’hydrostatique :

$$P(z_0+h)=P(z_0)-\rho \, g \, h$$

D’où :

$$ \begin{aligned} \vec{\pi}_A &= \vec{F}_{pb}+\vec{F}_{ph}\\ &= (P(z_0)-P(z_0+h) )\, S\, \vec{k}\\ &= \rho \, g \, {\color{#56C1FF} h \, S}\, \vec{k}\\ &= \rho \, g \, {\color{#56C1FF} V}\, \vec{k}\\ &= -\rho \, V \, \vec{g} \end{aligned} $$

On peut généraliser à tout corps :

$$\vec{\pi}_A = - \rho \, V \, \vec{g}$$

$\pi_A$ est la poussée d'Archimède (en $\pu{N}$)
$\rho$ est la masse volumique du fluide (en $\pu{kg*m-3}$)
$V$ est le volume immergé du corps (en $\pu{m3}$)
$g$ est la pesanteur (en $\pu{m*s-2}$)

⚠️

Si le corps flotte, $V$ désigne seulement
le volume de la partie immergée du corps !

🧊 Application 🧊

Quelle est la proportion immergée
du volume d’un glaçon ?

Données :

masse volumique de l'eau :
$\rho_\ell = \pu{1,0e3 kg*m-3}$
masse volumique de la glace :
$\rho_g = \pu{9,2e2 kg*m-3}$

Bilan des forces :

le poids du glaçon : $\vec{P}=m\vec{g}=\rho_g V_\mathrm{tot} \,\vec{g}$
la poussée d'Archimède : $\vec{\pi}_A = -\rho_\ell V_\mathrm{imm} \, \vec{g}$

On suppose que le glaçon est à l’équilibre.

Donc dans le référentiel terrestre supposé galiléen,
la 1^re loi de Newton nous informe que :

$$ \sum \vec{F}_\mathrm{ext} = \vec{0} $$

$\Rightarrow \vec{P}+\vec{\pi}_A= \vec{0}$

$\Leftrightarrow \rho_g V_\mathrm{tot} \, \vec{g} - \rho_\ell V_\mathrm{imm} \, \vec{g} = 0$

$\displaystyle \Rightarrow \frac{V_\mathrm{imm}}{V_\mathrm{tot}} = \frac{\rho_g}{\rho_\ell}$

92% du glaçon est immergé !

Question subsidiaire :

Qu’en est-il pour un iceberg dans l’océan 🚢 ?

Exercice

On tare la balance avant d’immerger la Tour Eiffel.

Que mesure alors la balance
après immersion de la Tour ?

Si système Tour Eiffel : La force de l’eau sur la Tour s’oppose à la force de la Tour sur l’eau d’après la 3e loi de Newton Et cette force est ensuite communiquée à la balance. Moralaité : la balance mesure la poussée d’Archimède sur la balance. Ou plutôt rho_eau*V = 1(en kg/L)*V(en L) puisqu’elle divise par g. -> Elle donne le volume !

On peut jouer sur le système aussi : {cristallisoir + eau + Tour + ficelle} BDF :

poids cristallisoir, poids eau, poids Tour
Force de soutien de la balance N
Force de tension sur la ficelle T

Comme on a taré avant la Tour, la balance indique zéro si N = -(P_eau + P_crist) Et pour le système {Tour + ficelle} T + P_Tour + πA = 0

Sur gros système : Pcrist + Peau + P_Tour + N + T = 0 -> N = - ( Pcrist + Peau + P_Tour + T ) <-> N = - (0 + P_Tour + (-P_Tour - πA) <-> N = πA

Conservation du débit volumique

Le débit volumique est le volume de fluide qui traverse une section droite du conduit où s’écoule le fluide
par unité de temps.

$$ D_V = \frac{V}{\Delta t} $$

Unité SI : $\pu{m3*s-1}$

Si $S$ est l'aire de la section droite et $v$ la vitesse
de l'écoulement à cet endroit, alors :

$$ {\color{#FF968D}D_V} = \frac{V}{\Delta t} = \frac{S\times v\times \Delta t}{\Delta t} = {\color{#FF968D}v\times S} $$

Rq :

Si la vitesse de l’écoulement n’est pas la même en tout point de la section (i.e. non uniforme sur une section), on peut remplacer $v$ par $\bar{v}$, la vitesse moyenne
sur la section.

Pour un fluide incompressible,
le débit se conserve.

Quel lien peut-on alors faire entre l’aire d’une section et la vitesse de l’écoulement si le conduit
où s’écoule le fluide est de section variable ?

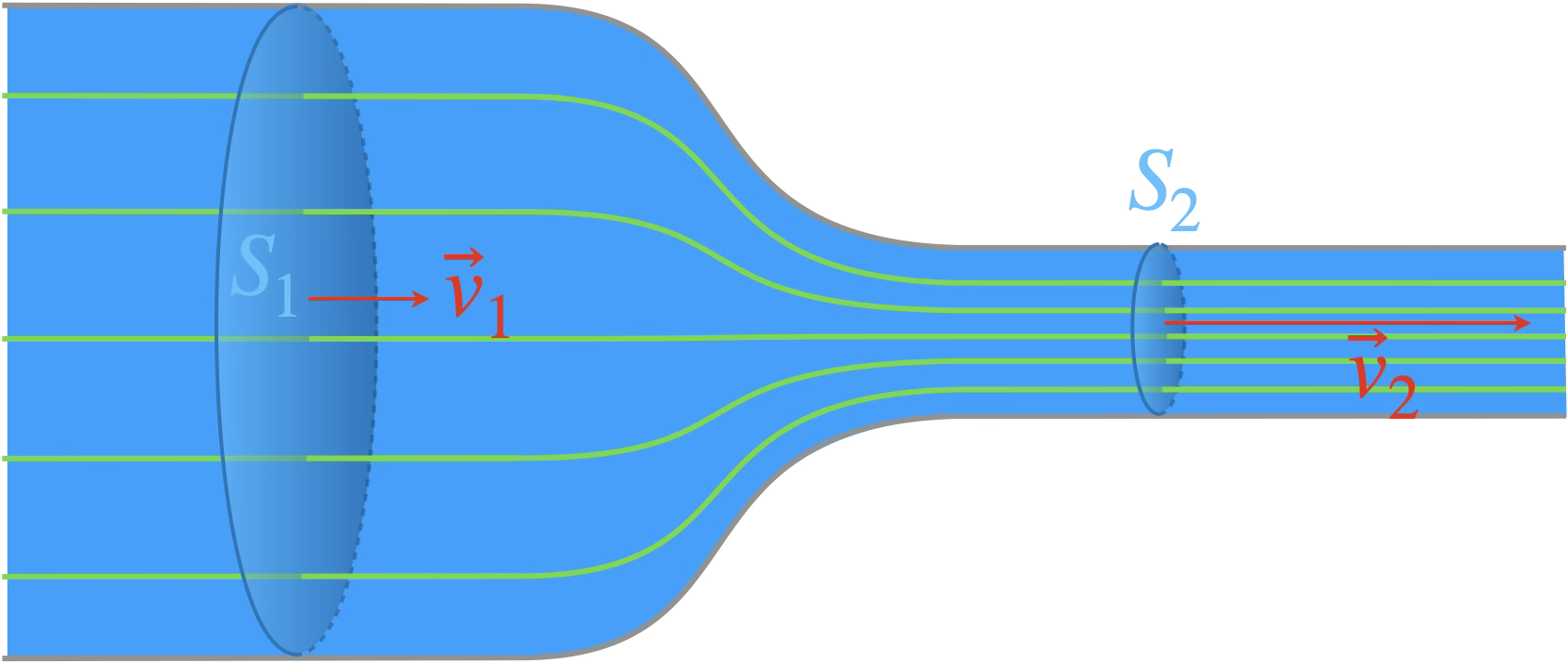
Par conservation du débit :

$${\color{#FF968D}v_1}\times {\color{#56C1FF}S_1} = {\color{#FF968D}v_2}\times {\color{#56C1FF}S_2}$$

La vitesse d'écoulement est inversement proportionnelle à l'aire de la section du conduit.

Fluide parfait

Un fluide est dit parfait si on peut décrire son écoulement sans prendre en compte
les effets de la viscosité.

En réalité, les seuls fluides réellement non visqueux sont l’hélium superfluide, les condensats de Bose-Einstein ou les plasmas quarks-gluons…

Mais en pratique, si les effets de la viscosité sont suffisamment faibles par rapports aux effets inertiels (liés à la vitesse), l'approximation de fluide parfait est adaptée (et d'autant plus qu'on est loin
d'un obstacle ou d'une paroi).

Écoulement permanent

Un écoulement en régime permanent (ou stationnaire) est un écoulement où la vitesse en chaque point ne varie pas au cours du temps.

Une ligne de courant d’un écoulement est
un chemin tangent au champ des vitesse.

Les lignes de courant permettent de cartographier
le champ de vitesse du fluide.

Relation de Bernoulli

L’écoulement d’un fluide incompressible parfait en régime permanent suit la relation de Bernoulli entre deux points $\mathrm{M_1}$ et $\mathrm{M_2}$ sur une ligne de courant :

$$ {\color{#73FDEA}P_1}+{\color{#FFF056}\rho g z_1} + {\color{#FF968D}\frac12 \rho v_1^{\,2}} = {\color{#73FDEA}P_2}+{\color{#FFF056}\rho g z_2}+ {\color{#FF968D}\frac12 \rho v_2^{\,2}} $$

Cette relation exprime la conservation de l’énergie volumique d’une particule de fluide :

$\frac12\rho v^2$ est une densité volumique d'énergie cinétique
$\rho g z $ est une densité volumique d'énergie potentielle de pesanteur
$P$ est une densité volumique d'énergie potentielle dont dérivent les forces de pression

Rq :

Cette conservation est valable
le long d’une ligne de courant.

Mais si l'écoulement est irrotationnel
(nul part dans le fluide, un petit moulinet ne se mettrait à tourner), elle est valable en tout point du fluide
(on dit que l'écoulement est potentiel).

Si le fluide est au repos ($v_1=v_2=0$), on retrouve
la loi fondamentale de la statique des fluides :

$$P_1+\rho g z_1 = P_2 + \rho g z_2$$

Et pour un écoulement horizontal
($z_1=z_2$), on obtient :

$$P_1+\frac12\rho v_1^{\,2}=P_2+\frac12\rho v_2^{\,2}$$

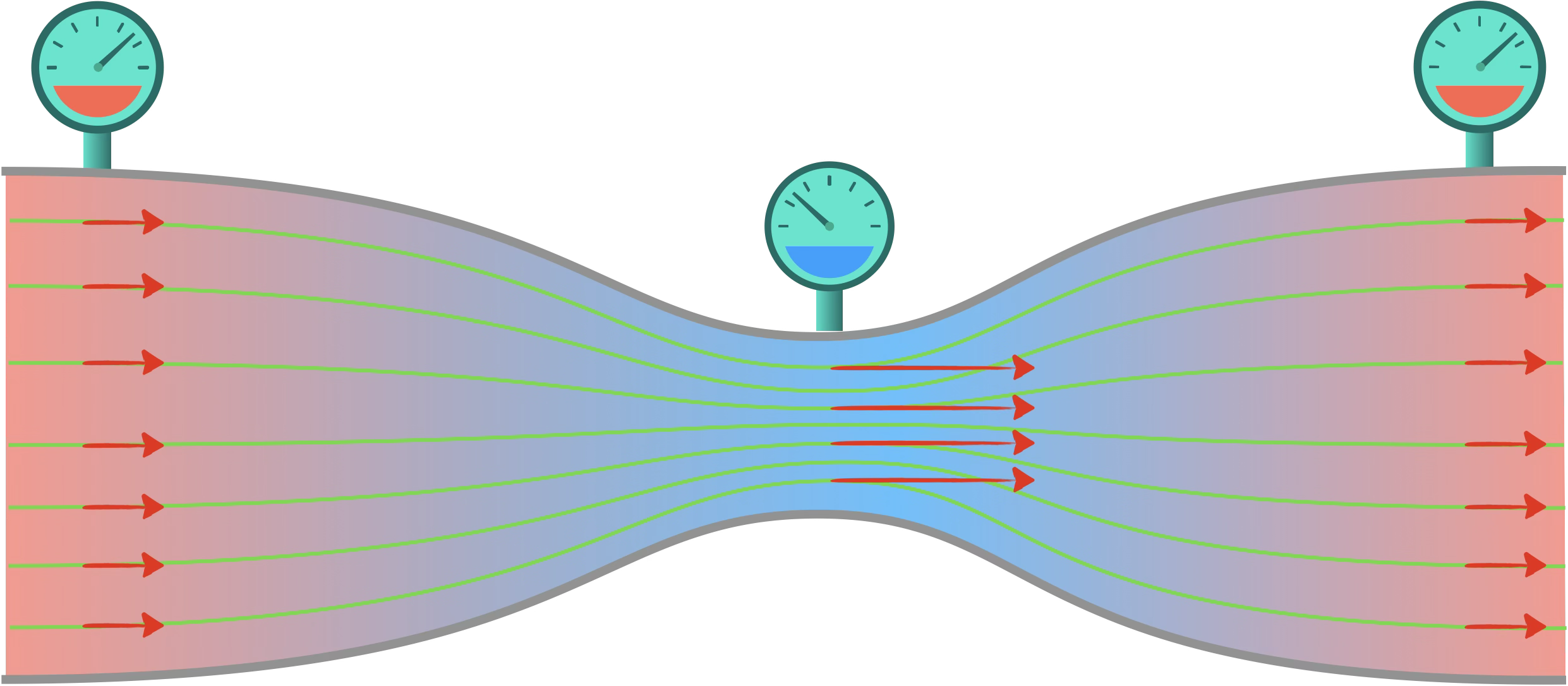
C'est l'effet Venturi.

L’effet Venturi indique donc que
si la vitesse de l’écoulement $\color{#FF968D}\nearrow$, alors la pression $\color{#56C1FF}\searrow$.

Or la conservation du débit volumique nous a appris que si l'écoulement devient plus étroit ($S$ $\color{#56C1FF}\searrow$),
alors sa vitesse $\color{#FF968D}\nearrow$.

On déduit donc que la pression $\color{#56C1FF}\searrow$
dans un étranglement.