Mouvement dans
un champ de gravitation

Les lois de Kepler

Johannes Kepler a énoncé trois lois empiriques concernant les mouvement des planètes autour
du Soleil qu’on peut étendre aux mouvements
des satellites autour des planètes.

Première loi – Loi des orbites

Dans le référentiel héliocentrique,
les trajectoires des planètes du système solaire sont des ellipses, dont le Soleil
occupe l'un des foyers.

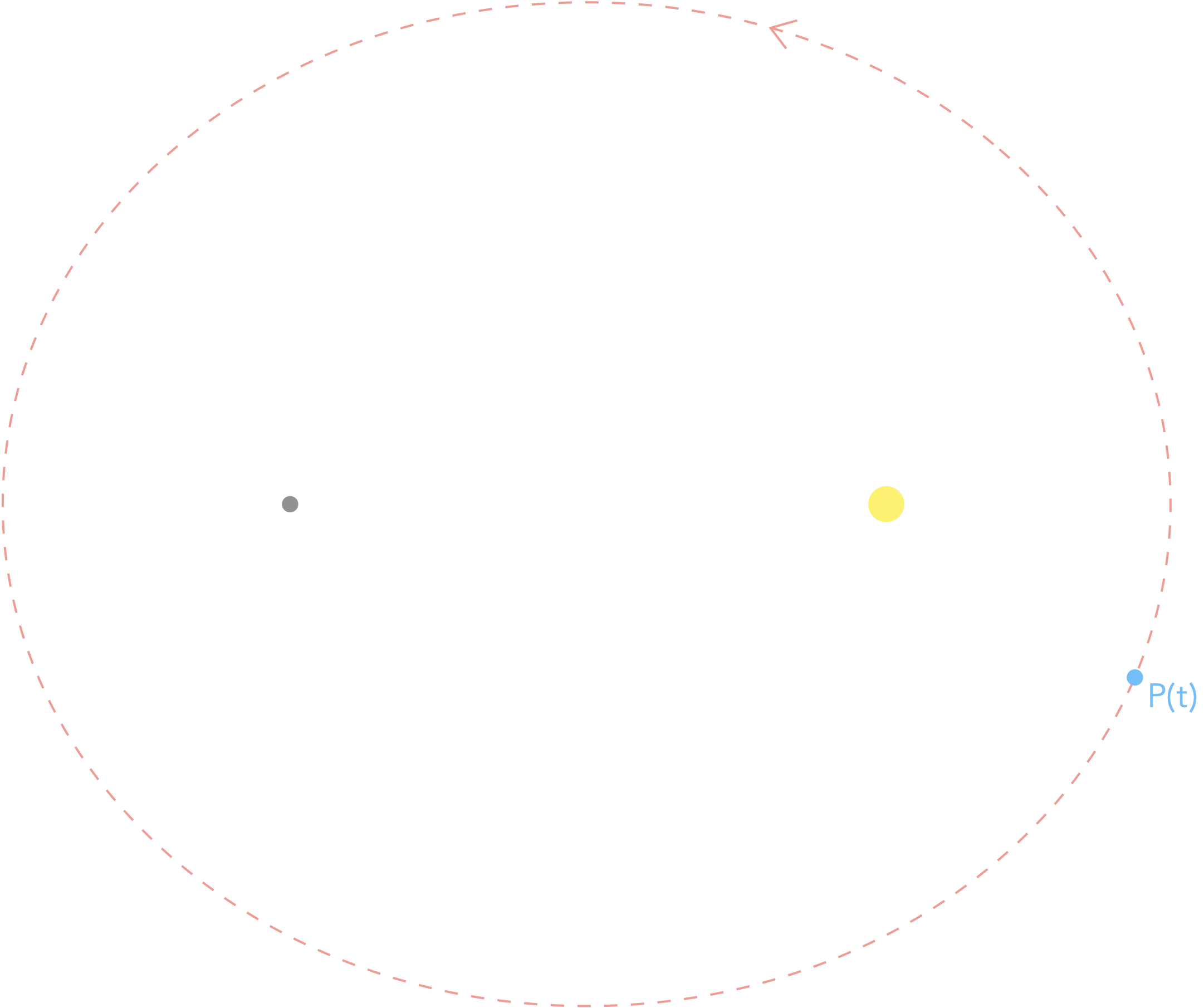
Une ellipse est une sorte de cercle applati.

Elle est caractérisée par son excentricité $e$
(écart au cercle) comprise entre 0 et 1.

La plus grande distance entre deux points
de l'ellipse est appelée grand axe et notée $2a$.

La plus petite distance entre deux points
de l'ellipse est appelée petit axe et notée $2b$.

  • $e=0$ $\rightarrow$ $a=b$


  • $ 0 < e < 1 \rightarrow a > b $

À part mercure, les planètes du système solaire
ont une très faible excentricité :

Mercure Vénus Terre Mars Jupiter Saturne Uranus Neptune
$e$ 0,2056 0,0068 0,0167 0,0934 0,0489 0,0565 0,0457 0,0113

Deuxième loi – Loi des aires

Le segment [SP] qui relie le centre P de la planète au centre S du Soleil balaie des aires égales
sur des durée égales.

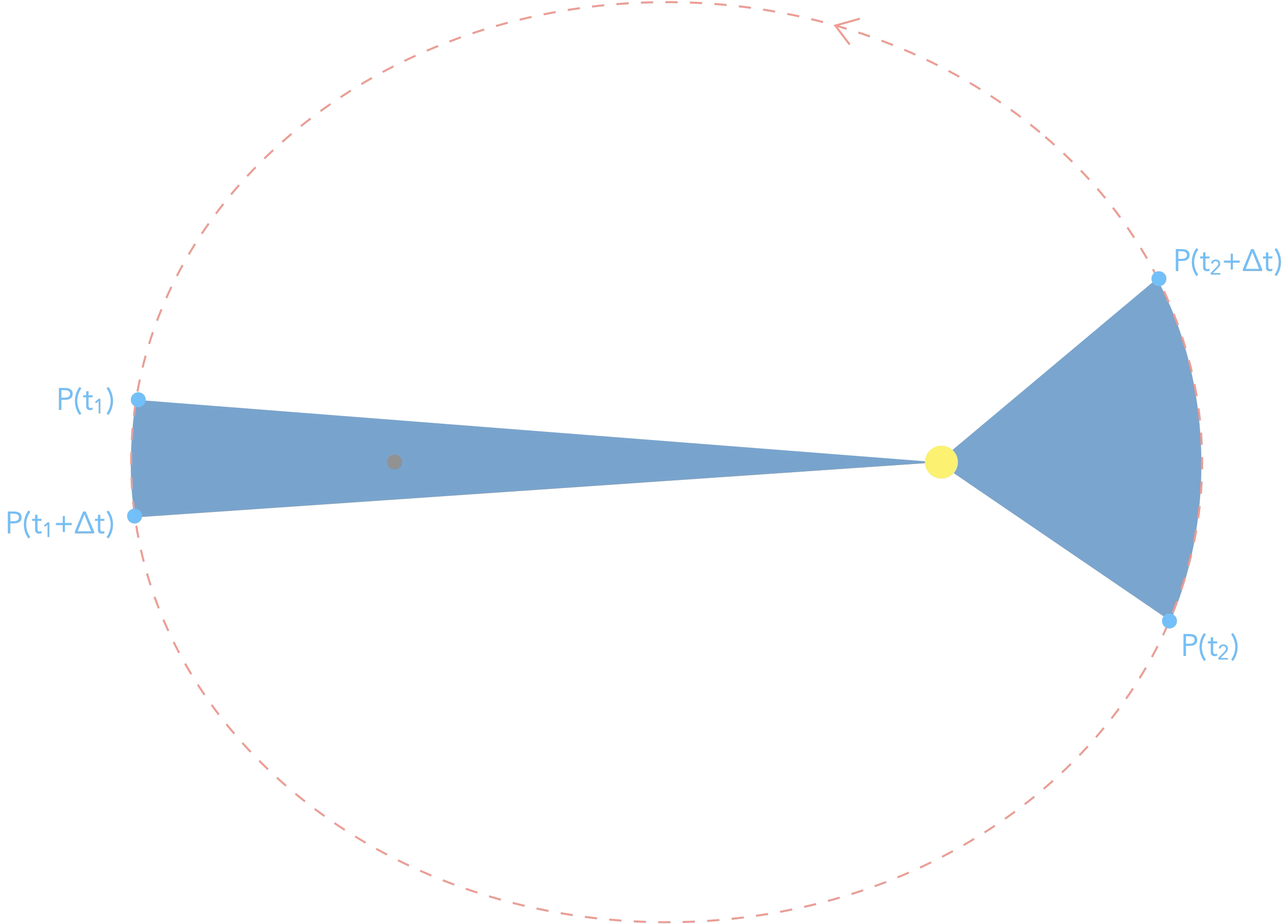
Conséquence sur la vitesse des planètes :

La vitesse de la planète évolue le long de son orbite
en fonction de la distance au Soleil :

  • elle est maximale au périhélie
    (point le plus proche du Soleil),
  • et minimale à l'aphélie
    (point le plus loin du Soleil).

Troisième loi – Loi des périodes

Le quotient du carré de la période de révolution $T$ d'une planète par le cube de la longueur $a$
du demi grand axe de son orbite est égal à une même constante pour toutes les planètes
du système solaire.

$$\frac{\color{#FFF056}T^2}{\color{#56C1FF}a^3} = \color{#88FA4E}k $$

Rq 1 :

La constante dépend de l’astre “central”.

Ainsi tous les satellites de la Terre partagent eux aussi un même quotient mais il est différent que pour
les planètes autour du soleil ($\frac{T^2}{a^3}=k'≠k$).

Rq 2 :

Ces lois ne sont qu’approximatives. Leur validité supposerait que la masse du Soleil soit infiniment
plus grande que celle des planètes.

En réalité, le petit astre ne tourne pas autour du gros mais les deux astres tournent autour
de leur centre de masse.

Système en orbite circulaire

D’après la loi d’interaction gravitationnelle, un astre
de masse $M_\mathcal{A}$ et de centre de masse O crée en tout point M de l’espace un champ de gravitation $\mathcal{G}$.

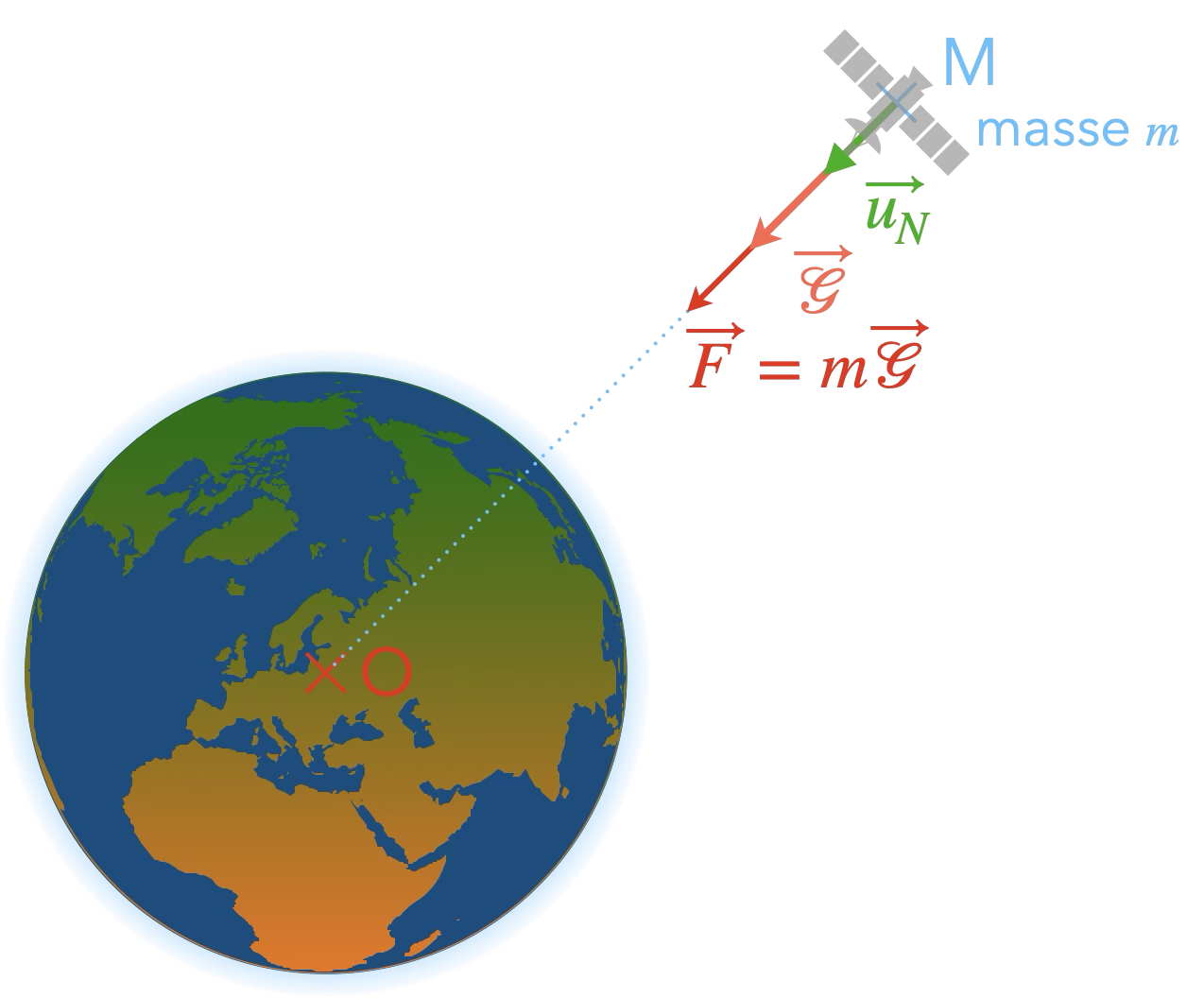
$\displaystyle\vec{\mathcal{G}}=$ $\displaystyle G\frac{M_\mathcal{A}}{\mathrm{OM}^2}\vec{u}_N$

  • $M_\mathcal{A}$ en kg
  • $\mathrm{OM}$ en m
  • $G=\pu{6,67E-11 N*m^2*kg^-2}$
  • $\vec{u}_N$ vecteur unitaire de direction (OM)
    orienté vers O.

Si un système de masse $m$ n’est soumis qu’à
l’attraction d’un seul astre de masse $M_\mathcal{A}$, le champ
est dit newtonien ; la seule force est la force d’interaction gravitationnelle $\vec{F}=m\vec{\mathcal{G}}$.

On se place dans un référentiel astrocentrique :

il est lié à l'astre de centre de masse O
et 3 étoiles lointaines supposées fixes.

Le référentiel astrocentrique est supposé galiléen.

Rq :
si l'astre est la Terre $\rightarrow$ référentiel géocentrique,
et pour le Soleil $\rightarrow$ référentiel héliocentrique.

La trajectoire du système de masse $m$ et de
centre de masse M est appelée orbite.

Étudions le mouvement de M
dans le cas d’une orbite circulaire.

Si $M_\mathcal{A}\gg m$, l'orbite pourra être considérée
comme centrée en O, le centre de l'astre.

La deuxième loi de Newton nous donne :

$ m{\color{#61D836}\,\vec{a}}={\color{#FF644E}m\,\vec{\mathcal{G}}}\Rightarrow $ $ {\color{#61D836}\,\vec{a}}=\color{#FF644E}\,\vec{\mathcal{G}} $

On décompose sur le repère de Frenet :

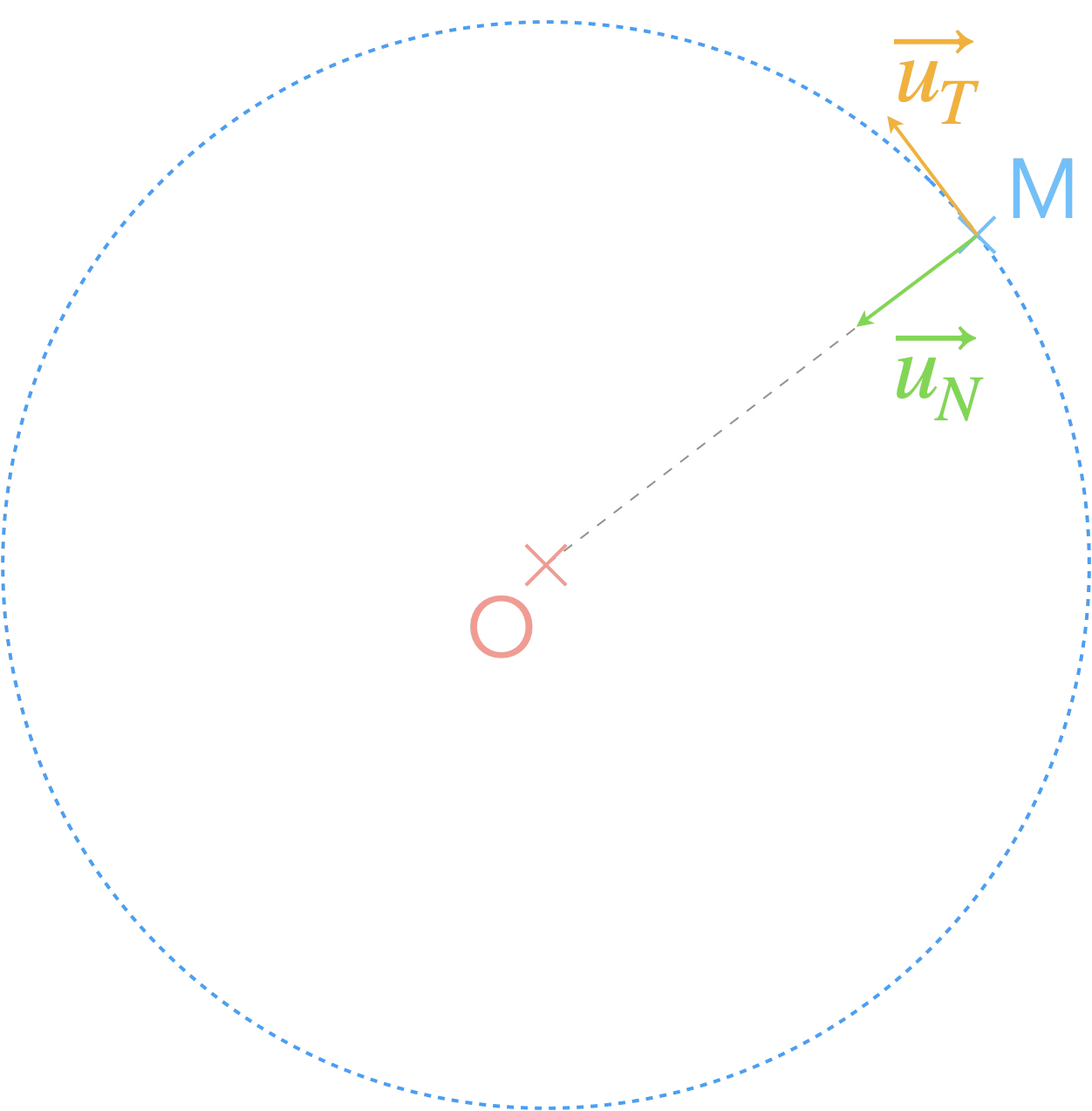
$$ \displaystyle \begin{cases} {\color{#61D836}a_T=\frac{\mathrm{d}v}{\mathrm{d}t}}=\color{#FF644E}0\\ {\color{#61D836}a_N = \frac{v^2}{R}} = \color{#FF644E}G\frac{M_\mathcal{A}}{R^2} \end{cases} $$

Rq : $R$ est le rayon de l'orbite ($R=\mathrm{OM}=\mathrm{cte}$).

On constante que le vecteur accélération
n’a pas de composante tangentielle.

$$ \vec{a}=G\frac{M_\mathcal{A}}{R^2}\vec{u}_N $$

On dit que l'accélération est centripète (vers le centre).

Et la norme de l'accélération
est constante.

De plus, à partir de

$$ \frac{\mathrm{d}v}{\mathrm{d}t} = 0, $$

on déduit que le mouvement est uniforme
($v(t)=\text{cste}$).

et de

$$ \frac{v^2}{R} = G\frac{M_\mathcal{A}}{R^2}, $$

on obtient la norme de la vitesse :

$\displaystyle v = $ $\displaystyle \sqrt{\frac{GM_\mathcal{A}}{R}}$

Le vecteur vitesse $\vec{v}$ du centre de masse M
d’un système en orbite circulaire s’écrit donc :

$$ \vec{v}=\sqrt{\frac{G M_\mathcal{A}}{R}} \, \vec{u}_T $$

Rq :
$\vec{v}$ ne dépend pas de la masse $m$ du système.

Période de révolution $T$

$T$ est la durée pour parcourir
l'orbite circulaire de rayon $R$.

On a donc :

$$ v\times T = 2\pi R $$

Prenons le carré de chaque membre :

$$ {\color{#FFD932}v^2} \times T^2 = 4\pi^2 R^2 $$
$$ {\color{#FFD932}\frac{G M_\mathcal{A}}{R}}\times T^2 = 4\pi^2 R^2 $$

Et en réarrangeant, on obtient :

$\displaystyle \frac{T^2}{R^3} = $ $\displaystyle\frac{4\pi^2}{G M_\mathcal{A}}$

Comme $\frac{T^2}{R^3}$ ne dépend pas de la masse $m$ du système, on vient de démontrer la troisième loi de Kepler
dans le cas d’une orbite circulaire.

Isolons $T$ :

$$ T = 2\pi \sqrt{\frac{R^3}{G M_\mathcal{A}}} $$

On constate que la période de révolution est d'autant plus grande que la distance à l'astre est grande.

On peut en déduire l’altitude
d’un satellite géostationnaire.

Un satellite géostationnaire est un satellite
immobile dans le référentiel terrestre.


  • Son orbite est circulaire,
  • dans le plan équatorial de la Terre,
  • et sa période vaut la période de rotation de la Terre.

Posons $R=(R_T+h)$ où $R_T$ est le rayon
terrestre et $h$ l’altitude du satellite
puis isolons $h$ dans la formule :

$$ \frac{T^2}{(R_T+h)^3} = \frac{4\pi^2}{{G}M_\mathrm{T}} $$

$\Downarrow$

$$ h = \sqrt[3]{\frac{{G}M_\mathrm{T} T^2}{4\pi^2}}-R_T $$

Application numérique

Données :

  • $M_\mathrm{T}=\pu{6,0E24 kg}$
  • $R_\mathrm{T}=\pu{6,4E6 m}$
$$ \begin{aligned} h&=\left(\frac{(\pu{6,67E-11)\times(\pu{6,0E24})\times( 24 \times 3600)^2 }}{4\pi^2}\right)^{\!\frac 13}-\pu{6,4E6}\\ &=\pu{3,6E7 m} \end{aligned} $$

Les satellites géostationnaires
orbitent à une altitude de 36 000 km.

Pourquoi n’est-ce pas réaliste ?

(à part la présence de frottements)

Car tout objet qui orbite un “caillou” près
de sa surface le fait en environ 1h30 !

En effet, supposons une boule rocheuse de densité uniforme égale à 5 (densité moyenne de la Terre).

On a alors $\rho\approx\pu{5E3 kg*m-3}$
et la masse de l'astre vaut
$M = \rho\times V= \rho\times\frac 43 \pi R^3$

Or on a obtenu plus haut :

$$T^2 = \frac{4\pi^2 R^3}{GM}$$

En remplaçant M :

$$T^2 = \frac{4\pi^2 R^3}{G \rho \frac 43 \pi R^3}$$

Et après simplification :

$$T^2 = \frac{3\pi }{G \rho}$$

Soit

$\displaystyle T = \sqrt{\frac{3\pi}{G\rho}}$

Le résultat ne dépend plus de $R$ !!

Pour toute boule d'approximativement
la même densité, on aura la même période
de révolution $T$ près de sa surface !

A.N. :

$T\displaystyle =\frac{3\pi}{\pu{6,67e-11}\times\pu{5,0e3}}$
$\approx \pu{5E3 s}$

Soit entre 1h et 2h.

Si Obelix recommence la même expérience sur la Lune, il devrait trouver un temps comparable.

Et si Obelix lance le javelot plus fort ?

On change d'orbite (plus circulaire) !

Et s'il envoie le javelot à plus de 11,2 km/s (vitesse
de libération), le javelot s'en va pour toujours ! Il échappe à l'attraction gravitationnelle de la Terre.

Retour site