Force des acides
et des bases

Autoprotolyse de l’eau

L’eau est un ampholyte.

Les deux couples acide-base
auxquels l'eau appartient sont :

$$({\color{#88FA4E}\ce{H2O}}/{\color{#56C1FF}\ce{HO^-}})$$

$$({\color{#FF968D}\ce{H3O+}}/{\color{#88FA4E}\ce{H2O}})$$

L’eau peut donc réagir sur elle-même !
C’est la réaction d’autoprotolyse de l’eau.

Équation de la réaction :

$$\ce{{\color{#88FA4E}\ce{H2O}}(ℓ) + {\color{#88FA4E}\ce{H2O}}(ℓ) -> {\color{#FF968D}\ce{H3O+}}(aq) + {\color{#56C1FF}\ce{HO^-}}(aq)}$$

La constante d’équilibre de cette réaction, aussi appelée produit ionique de l’eau s’écrit :

$${\color{#FFF056}K_\mathrm{e}} = \frac{\ce{[{\color{#FF968D}\ce{H3O+}}]}\times\ce{[{\color{#56C1FF}\ce{HO^-}}]}}{{C^\mathrm{o}}^2}$$

À 25°C, $K_\mathrm{e}=\pu{1,0e-14}$,
d'où $\mathrm{p}K_\mathrm{e} =$ $-\log\left(K_\mathrm{e}\right)=$ $14$.

Si on connaît $K_\mathrm{e}$, la concentration en ions oxonium permet de déterminer celle en ions hydroxyde
et inversement.

Exemple :

Le pH d’une solution à 25°C est mesurée à 2,3.

Déterminer la concentration en ions oxonium
et en ions hydroxyde.

$\begin{aligned} \ce{[H3O+]}&=10^{- \mathrm{pH}}\\ &= 10^{-2,3}\\ &= \pu{5,0e-3 mol*L-1} \end{aligned}$

$\begin{aligned} \ce{[HO^-]}&=\frac{K_\mathrm{e} \times{C^\mathrm{o}}^2}{\ce{[H3O+]}}\\ &= \frac{\pu{1,0e-14\times 1,0}}{\pu{5,0e-3}}\\ &= \pu{2,0e-12 mol*L-1} \end{aligned}$

On peut déduire de $K_\mathrm{e}$ le pH
d’une solution acide, neutre ou basique.

Si la solution est neutre

On a par définition :
$\ce{[{\color{#FF968D}\ce{H3O+}}]=[{\color{#56C1FF}\ce{HO^-}}]}$

Et comme $\displaystyle\frac{\ce{[{\color{#FF968D}\ce{H3O+}}}]\times[{\color{#56C1FF}\ce{HO^-}}]}{{C^\mathrm{o}}^2}={\color{#FFF056}K_\mathrm{e}}$

on obtient $\ce{[{\color{#FF968D}\ce{H3O+}}]}^2 = {\color{#FFF056}K_\mathrm{e}} \times {C^\mathrm{o}}^2 $

Finalement :

$\begin{aligned} \ce{[{\color{#FF968D}\ce{H3O+}}]} &= \sqrt{{\color{#FFF056}K_\mathrm{e}} \times {C^\mathrm{o}}^2}\\ &= \sqrt{{\color{#FFF056}K_\mathrm{e}}}\times {C^\mathrm{o}} \\ &= \pu{1,0e-7 mol*L-1} \end{aligned} $

Ou encore :
$ \displaystyle\mathrm{pH} = \frac{1}{2}\mathrm{p}K_\mathrm{e} = 7,0 $

Si la solution est acide

$\ce{[{\color{#FF968D}\ce{H3O+}}]>[{\color{#56C1FF}\ce{HO^-}}]}$

Et donc $\displaystyle\ce{[{\color{#FF968D}\ce{H3O+}}]}>\frac{{\color{#FFF056}K_\mathrm{e}}\times {C^\mathrm{o}}^2}{\ce{[{\color{#FF968D}\ce{H3O+}}]}}$

$\displaystyle \Rightarrow\ce{[{\color{#FF968D}\ce{H3O+}}]}^2>{\color{#FFF056}K_\mathrm{e}}\times {C^\mathrm{o}}^2$

$\displaystyle \Rightarrow\ce{[{\color{#FF968D}\ce{H3O+}}]}> \sqrt{{\color{#FFF056}K_\mathrm{e}}}\times {C^\mathrm{o}}$

d'où $\displaystyle \ce{[{\color{#FF968D}\ce{H3O+}}]}> \pu{1,0e-7 mol*L-1}$

Ou encore $\displaystyle \mathrm{pH}<\frac{1}{2}{\color{#FFF056}\mathrm{p}K_\mathrm{e}}$
Soit $\displaystyle \mathrm{pH}<7,0$

Si la solution est basique

$\ce{[{\color{#FF968D}\ce{H3O+}}]<[{\color{#56C1FF}\ce{HO^-}}]}$

$\displaystyle \Rightarrow \ce{[{\color{#FF968D}\ce{H3O+}}]}< \pu{1,0e-7 mol*L-1}$

Soit $\displaystyle \mathrm{pH}>7,0$

Acides forts et bases fortes

Un acide fort ou une base forte réagissent
de manière quasi-totale avec l'eau.

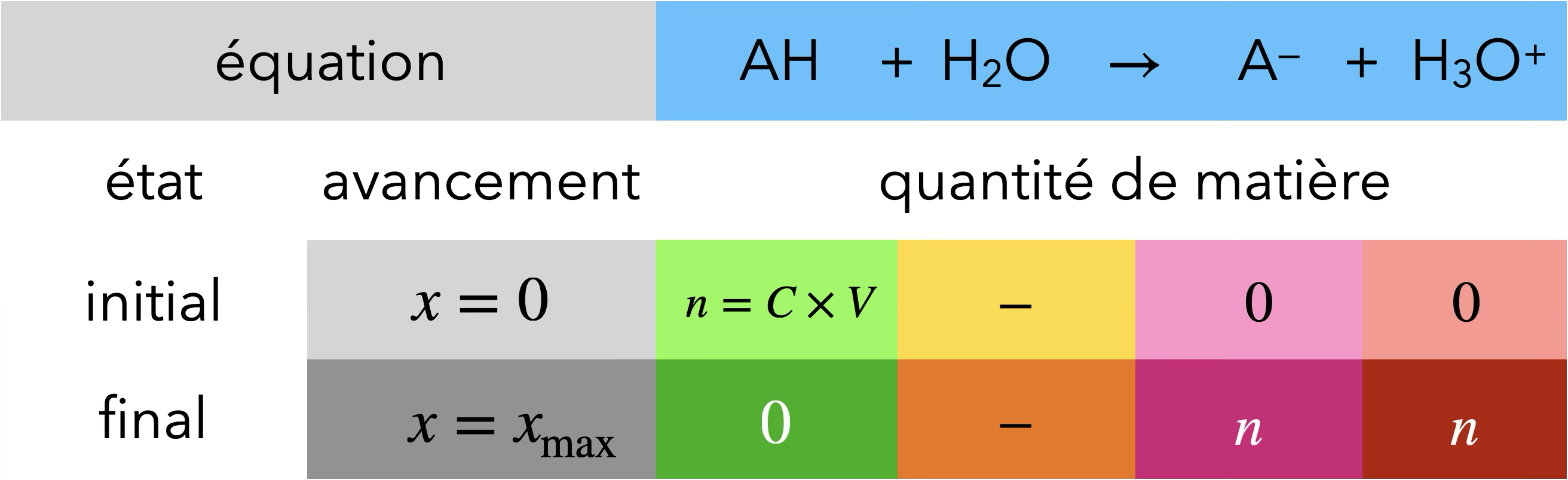
$\ce{{\color{#FF968D}AH} + H2O ->}$ $\ce{A- + H3O^+}$

Si $\ce{AH}$ est un acide fort

$\tau=$ $1$

(où $\tau$ est le taux d'avancement de la réaction)

D’où ${\color{#FF968D}\ce{[H3O^+]}} = \ce{[AH]_0} = {\color{#FF968D}C}$

La concentration en ions oxonium en solution est
égale à la concentration apportée $C$ en acide.

$\Rightarrow\mathrm{pH}=$ $\displaystyle -\log\left(\frac{C}{C^\mathrm{o}}\right)$

${\color{#56C1FF}\ce{A^-}} \ce{+ H2O ->}$ $\ce{AH + HO^-}$

Si $\ce{A-}$ est une base forte, $\tau= 1$

D'où ${\color{#56C1FF}\ce{[HO^-]}} \ce{= [A^-]_0} = {\color{#56C1FF}C}$
la concentration en ions hydroxyde est égale
à la concentration apportée $C$ en base.

$\Rightarrow\mathrm{pH}=$ $\displaystyle 14 +\log\left(\frac{C}{C^\mathrm{o}}\right)$

En effet :

$$K_e =\frac{\ce{[H3O+]\times [HO-]} }{{C^\circ}^2}$$

$$ \begin{aligned} \Rightarrow \ce{[H3O+]}&=\frac{K_e {C^\circ}^2}{\ce{[HO-]}}\\ &=\frac{K_e {C^\circ}^2}{\color{#FFD932}C} \end{aligned} $$

$$ \begin{aligned} \Rightarrow \mathrm{pH} &=-\log\left(\frac{\ce{[H3O+]}}{C^\circ}\right)\\ &=-\log\left(K_e\times\frac{C^\circ}{\color{#FFD932}C}\right)\\ &=-\left( \log\left(K_e\right)+\log\left(\frac{C^\circ}{\color{#FFD932}C}\right)\right)\\ &=\mathrm{p}K_e + \log\left(\frac{\color{#FFD932}C}{C^\circ}\right) \end{aligned} $$

Exemples d’acides forts :

l'acide chlorhydrique $\ce{HCℓ(g)}$
$\ce{HCℓ(g) + H2O(ℓ) -> H3O^+(aq) + Cℓ^-(aq)}$

l'acide nitrique $\ce{HNO3(ℓ)}$
$\ce{HNO3(ℓ) + H2O(ℓ) -> H3O^+(aq) + NO3^-(aq)}$

Exemple de base forte :

l'hydroxyde de sodium ou soude $\ce{NaOH(s)}$
$\ce{NaOH(s) + H2O(ℓ) -> HO^-(aq) + Na^+(aq)}$

Acides faibles et bases faibles

La transformation chimique entre un acide faible
ou une base faible et l’eau n’est pas totale.

$\ce{{\color{#FF968D}AH} + H2O <=> A- + H3O^+}$

Si $\ce{AH}$ est un acide faible

$\tau$ $<1$

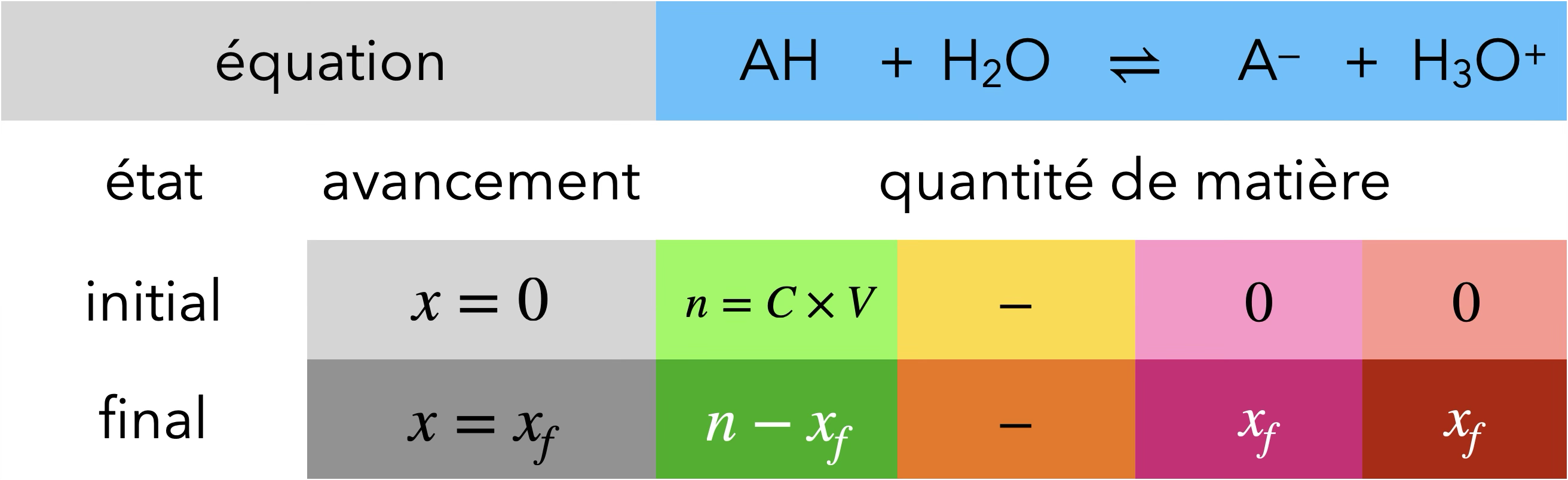
$$ \begin{aligned} x_f < n &\Rightarrow \ce{[H3O+] < C}\\ & \Rightarrow {\color{#FF968D} \mathrm{pH} > -\log\left(\frac{C}{C^\mathrm{o}}\right) } \end{aligned} $$

Le pH d'un acide faible dans l'eau est plus grand que celui d'un acide fort de même concentration apportée.

${\color{#56C1FF}\ce{A^-}}\ce{ + H2O -> AH + HO^-}$

Si $\ce{A-}$ est une base faible, $\tau < 1$

Le pH d'une base faible dans l'eau est
plus faible que celui d'une base forte
de même concentration apportée.

En effet :

$\ce{[HO-]}\searrow$ $\Rightarrow$ $\ce{[H3O+]}\nearrow$ $\Rightarrow$ $\mathrm{pH}\searrow$

Exemple d’un acide faible :

l'acide éthanoïque $\ce{CH3COOH(ℓ)}$
(ou acide acétique)
Sa forme dissoute est simplement $\ce{CH3COOH(aq)}$.
$\ce{CH3COOH(ℓ) + H2O(ℓ) <=> H3O^+(aq) + CH3COO^-(aq)}$
Sa base conjuguée est l'ion éthanoate.

Exemple d’une base faible :

l'ammoniac $\ce{NH3(g)}$
Sa forme dissoute est simplement $\ce{NH3(aq)}$.
$\ce{NH3(g) + H2O(ℓ) <=> HO^-(aq) + NH4^+(aq)}$
Son acide conjugué est l'ion ammonium.

Force d’un acide faible
ou d’une base faible

$$\ce{{\color{#FF968D}AH} + H2O <=> A- + H3O^+}$$

La constante d’équilibre de la réaction d’un acide faible dans l’eau s’appelle constante d’acidité notée $K_\mathrm{A}$.

$K_\mathrm{A}$ caractérise un couple acide-base $({\color{#FF968D}\ce{AH}}/{\color{#56C1FF}\ce{A-}})$.

Par définition,

${\color{#FF968D}K_\mathrm{A}}=$ $\displaystyle\frac{\ce{[A-]_\mathrm{f} \times[H3O+]_\mathrm{f} }}{[{\color{#FF968D}\ce{AH}}]_\mathrm{f}\times C^\mathrm{o}}$

Pour comparer la force des acides faibles, ou la force des bases faibles, on compare leurs $K_\mathrm{A}$ ou plutôt leurs $\mathrm{p}K_\mathrm{A}$ qui permettent de manipuler des valeurs plus pratiques (généralement entre 0 et 14).

$\displaystyle\mathrm{p}K_\mathrm{A}=-\log\left(K_\mathrm{A}\right)$

Plus la réaction d’un acide faible sur l’eau est avancée,

plus $\tau$ est proche de 1

plus $K_\mathrm{A}$ est grand

plus $\mathrm{p}K_\mathrm{A}$ est faible

${\color{#56C1FF}\ce{A^-}}\ce{ + H2O <=> AH + HO^-}$

Pour une base faible, la constante d’équilibre
de sa réaction avec l’eau s’écrit :

$$ \begin{aligned} {\color{#56C1FF}K_\mathrm{B}}&=\frac{\ce{[AH]\times[HO-]}}{[{\color{#56C1FF}\ce{A^-}}]\times C^\mathrm{o}}\\ &=\frac{\ce{[AH]}\times {\color{#FFF056}K_\mathrm{e}\times {C^\mathrm{o}}^2}}{[{\color{#56C1FF}\ce{A^-}}]\times C^\mathrm{o}\times {\color{#FFF056}\ce{[H3O+]}}}\\ &= \frac{\color{#FFF056}K_\mathrm{e}}{\color{#FF968D}K_\mathrm{A}} \end{aligned} $$

Plus la réaction d’une base faible sur l’eau est avancée,

plus $\tau$ est proche de 1

plus $K_\mathrm{B}$ est grand

plus $K_\mathrm{A}$ est petit

plus $\mathrm{p}K_\mathrm{A}$ est grand

Donc plus un acide faible est fort
(plus il réagit avec l’eau),
plus son $\mathrm{p}K_\mathrm{A}$ est faible.

À l'inverse,
plus une base faible est forte
(plus elle réagit avec l'eau),
plus son $\mathrm{p}K_\mathrm{A}$ est grand.

Pour le couple $({\color{#FF968D}\ce{H3O+}}/{\color{}\ce{H2O}})$, que vaut $K_\mathrm{A}$ ?

$${K_\mathrm{A}} = 1$$

Et $\mathrm{p}K_\mathrm{A}$ ?

$$\mathrm{p}K_\mathrm{A} = 0$$

Pour le couple $({\color{}\ce{H2O}}/{\color{#56C1FF}\ce{HO-}})$, que vaut $K_\mathrm{A}$ ?

$${K_B} = 1$$

$$\Rightarrow {K_\mathrm{A}} = \frac{\color{#FFF056}K_\mathrm{e}}{\color{#56C1FF}K_B}=10^{-14}$$

Et $\mathrm{p}K_\mathrm{A}$ ?

$$\mathrm{p}K_\mathrm{A} = 14$$

On classe les acides et les bases
sur une échelle de pK_A.

$\ce{NH4+}$ est un acide plus faible / fort que $\ce{CH3COOH}$

$\ce{NH3}$ est une base plus faible / forte que $\ce{CH3COO-}$

Diagramme de distribution

La proportion à l’équilibre
d’un acide $r_\mathrm{AH}$ est le quotient :

$${\color{#FF968D} r_\mathrm{AH}}=\frac{\color{#FF968D} n_\mathrm{AH,f}}{{\color{#FF968D}{n_\mathrm{AH,f}}}+{\color{#56C1FF}n_\mathrm{A^-,f}}}$$

Et celle de sa base conjuguée :

$${\color{#56C1FF} r_\mathrm{A^-}}=\frac{\color{#56C1FF} n_\mathrm{A^-,f}}{{\color{#FF968D}{n_\mathrm{AH,f}}}+{\color{#56C1FF}n_\mathrm{A^-,f}}}$$

Dans un diagramme de distribution, on superpose les courbes donnant la proportion à l’équilibre en quantité d’un acide et de sa base conjuguée en fonction du pH.

Diagramme de prédominance

Le diagramme de prédominance est une simplification du diagramme de distribution. On n’indique plus que l’espèce qui prédomine sur un axe de pH :

pour $\mathrm{pH < pK_A}$, $\mathrm{{\color{#FF968D}[AH]}>{\color{#56C1FF}[A^-]}}$
pour $\mathrm{pH = pK_A}$, $\mathrm{{\color{#FF968D}[AH]}={\color{#56C1FF}[A^-]}}$
pour $\mathrm{pH > pK_A}$, $\mathrm{{\color{#FF968D}[AH]}<{\color{#56C1FF}[A^-]}}$

Exemples :

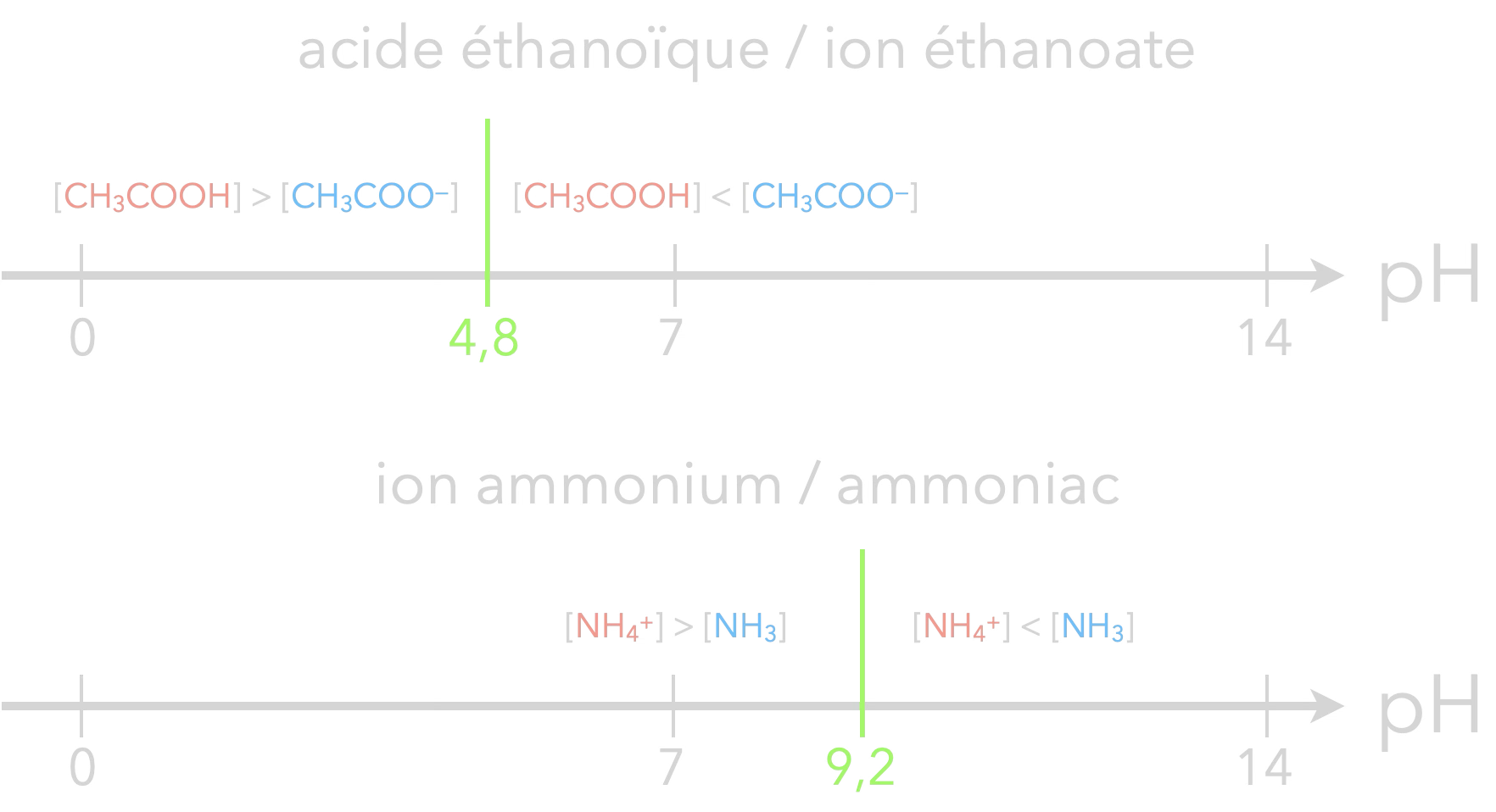
Rq :

L’acide d’un couple peut très bien dominé sa base conjuguée dans une solution aqueuse basique
et réciproquement, une base peut dominer
dans une solution acide !

Indicateur coloré

Un indicateur coloré est un couple acide-base
dont la forme acide et la forme basique
n’ont pas la même couleur.

La zone de virage d’un indicateur coloré
est la zone de pH où les formes acides et basique
sont en proportions similaires.

La couleur de l'indicateur coloré dans la zone de virage est alors un mélange des couleurs acide et basique.

La zone de virage intervient pour $\mathrm{pH}=$ $\mathrm{pK_A}$.

Les diagramme de prédominance permettent de caractériser efficacement un indicateur coloré.

Pour utiliser efficacement un indicateur coloré
lors d’un titrage ayant pour support une réaction
acide-base, il faut que la zone de virage
contienne le pH à l’équivalence pH_E.

Exemple : choisir un indicateur coloré
adapté au titrage ci-après.

On retrouve des indicateurs colorés sur
les bandelettes et papier pH…

… et dans la nature.

Hortensias (Hydrangea macrophylla) Sol Calcaire Basique / Alcalin (pH>7) Rose à Rouge (chez nous) Sol Granitique Acide (pH<5,5) Bleu à Violet (en Bretagne)

Contrairement à une idée reçue, ce n’est pas l’acidité elle-même qui colore les fleurs en bleu, mais la présence d’ions aluminium (Al3+).

En sol acide (granitique) : L’aluminium présent dans la terre devient soluble. La plante l’absorbe, et celui-ci se lie à un pigment de la fleur (la delphinidine-3-glucoside), ce qui produit la couleur bleue.

En sol basique (calcaire) : L’aluminium reste “prisonnier” sous forme de précipités insolubles. La plante ne peut pas l’assimiler, et le pigment reste dans sa forme naturelle, qui est rose.

Dans un sol calcaire, le carbonate de calcium réagit avec les ions H+ pour les neutraliser = effet tampon. Dans un sol granitique, ce tampon est absent. Les pluies, naturellement légèrement acides à cause du CO 2 dissous (acide carbonique), font donc chuter le pH du sol sans résistance.

Pour forcer un hortensias rose à devenir bleu dans un jardin calcaire, il ne suffit pas d’acidifier le sol (avec de la terre de bruyère) ; il faut souvent ajouter du “bleuissant” (sulfate d’alumine) pour fournir l’aluminium manquant.

Acide $\alpha$-aminé

Qu’ont de communs ces acides α-aminés ?

un groupe carboxyle
un groupe amine

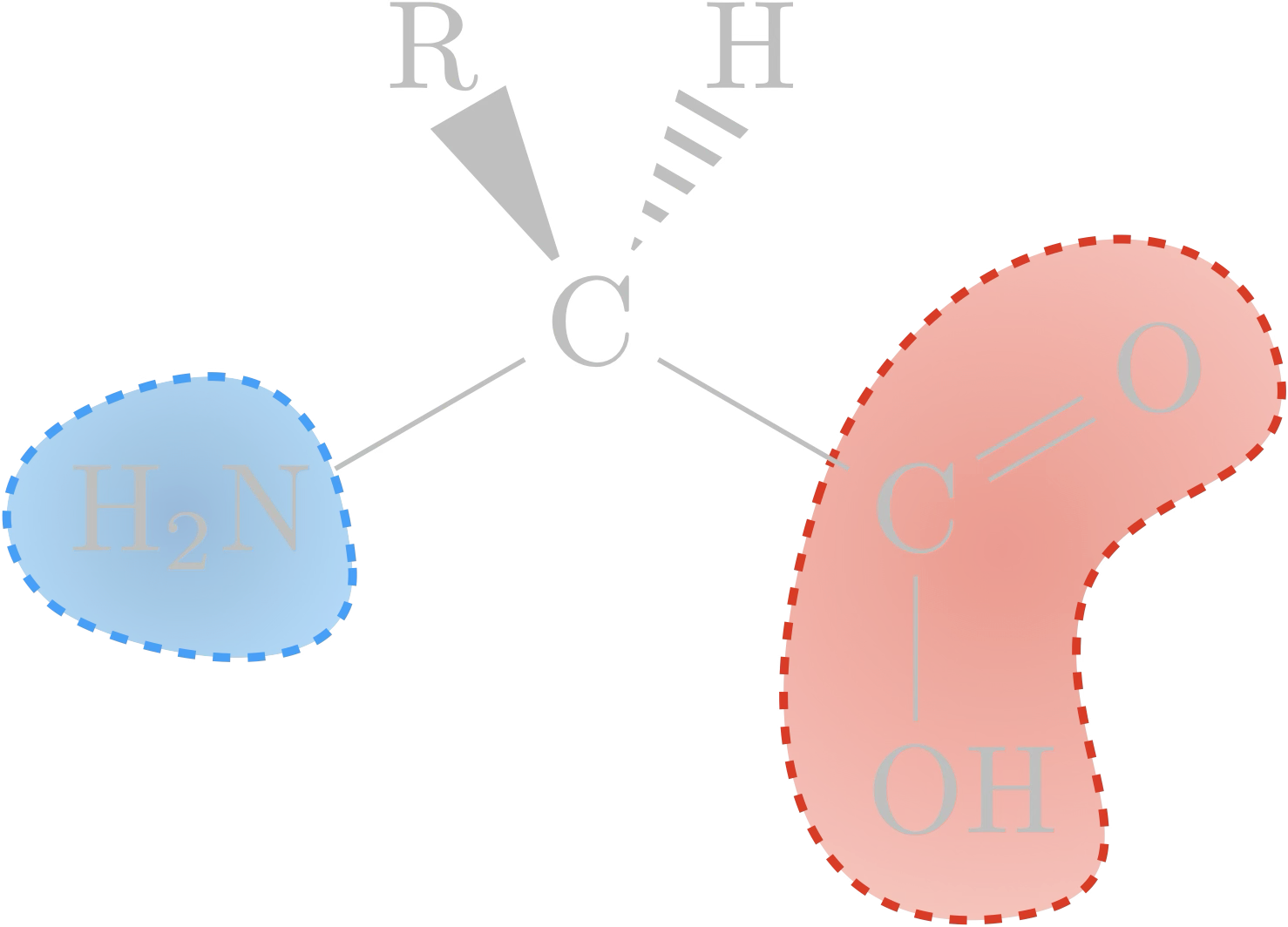
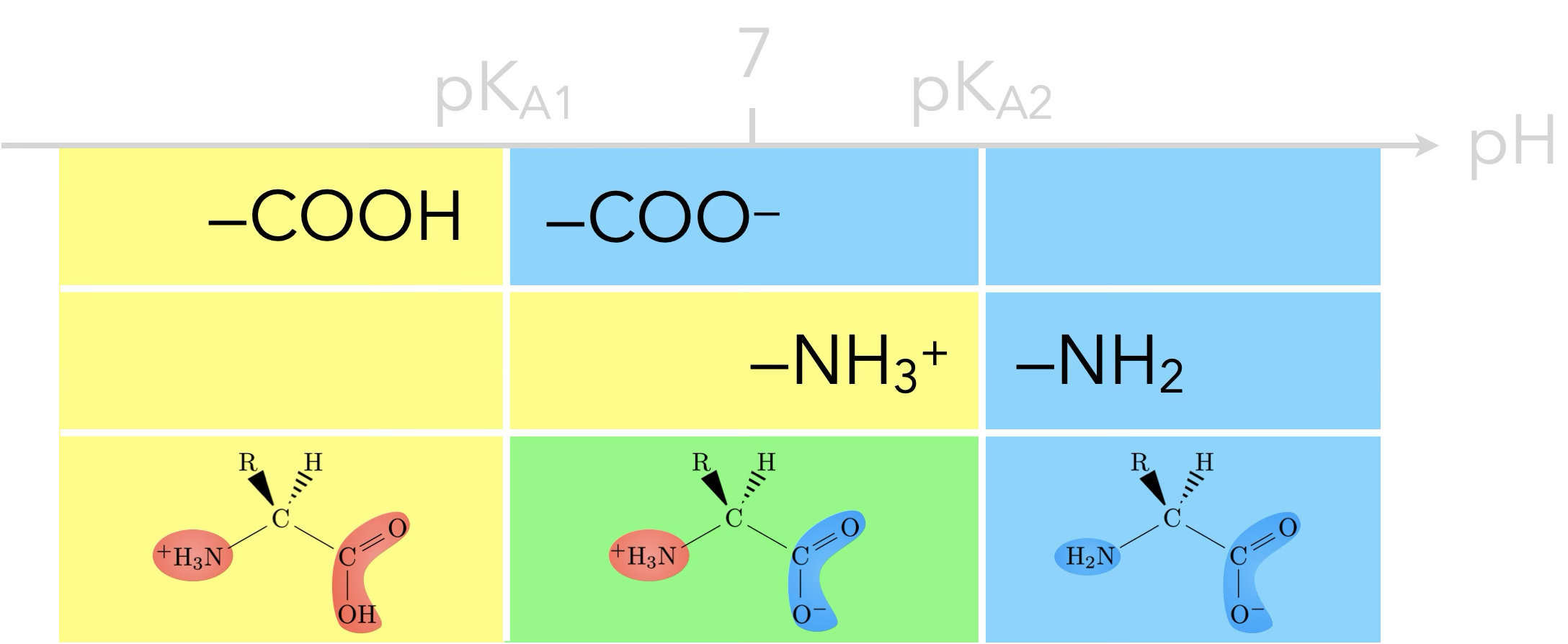
Les acides aminés sont donc des amphotères car ils interviennent à la fois dans le couple acide-base acide carboxylique ($\ce{-COOH}$) / ion carboxylate ($\ce{-COO^-}$) de constante d’acidité $\mathrm{K_{A1}}$ et le couple ion ammonium
($\ce{-NH3^+}$) / amine ($\ce{-NH2}$) de constante $\mathrm{K_{A2}}$,
avec $\mathrm{pK_{A1}<pK_{A2}}$.

Diagramme de prédominance d’un acide aminé :

Au pH de l’organisme, un acide aminé
est donc une espèce ampholyte.

Et cette forme est doublement ionique.
On parle de zwitterion ou de dipôle ionique.

Ça garantit une excellente solubilité dans le sang et
le cytoplasme grâce aux fortes liaisons ion-dipôle
avec les molécules d'eau.

Cela permet surtout la formation de liaisons ioniques
à l'intérieur de la structure tertiaire de la protéine.

🦺 Hors-programme ⚠️

À l'exception de la glycine, le carbone sur lequel se trouve le groupe amino a 4 liaisons différentes.
On parle alors de carbone asymétrique.

La présence de carbone asymétrique donne à la molécule une propriété particulière : la chiralité. Une molécule chirale n'est pas superposable à son image dans un miroir (comme une main, d'où le nom).

Deux molécules chirales images l'une de l'autre
dans un miroir sont appelées énantiomères
(c'est un exemple d'isomérie de configuration).

Dans un environnement achiral, ça ne change rien (mêmes températures de changement d'état, même densité, etc.), mais dans un environnement chiral,
ces molécules peuvent se comporter de manière radicalement différente.

Ex : la carvone est une molécule chirale dont les deux formes interagissent différemment avec les récepteurs olfactifs de notre nez (qui sont eux-mêmes composés de protéines chirales).

Un exemple plus sinistre : la thalidomide,
un médicament des années 50.

La thalidomide était vendue comme un mélange racémique (mélange 50/50 des deux énantiomères).

L'énantiomère (R) possède les propriétés recherchées, à savoir un effet sédatif et anti-nauséeux, très efficace pour les femmes enceintes souffrant de nausées matinales.
L'énantiomère (S) s'est révélé être un agent tératogène extrêmement puissant, provoquant de graves malformations congénitales chez les fœtus.

Le scandale de la thalidomide (commercialisée sous le nom de Contergan en Europe) est considéré comme la plus grande catastrophe médicale d’origine humaine. Si ses effets tératogènes (induisant des malformations fœtales) n’ont pas été détectés à l’époque, c’est en raison d’une combinaison de lacunes réglementaires, de croyances scientifiques erronées et de pièges biologiques.

Dans les années 1950, la réglementation pharmaceutique était embryonnaire. Priorité à la toxicité aiguë : Les tests se concentraient sur la dose létale. Comme il était presque impossible de tuer un rat avec de la thalidomide, le médicament a été déclaré “incroyablement sûr”. Pas de tests de tératogénicité : Il n’était tout simplement pas obligatoire de tester l’effet d’une molécule sur le développement du fœtus ou sur les femelles gestantes avant la mise sur le marché.

À cette époque, la communauté scientifique était convaincue que le placenta agissait comme un filtre absolu, protégeant le fœtus de toute substance nocive présente dans le sang maternel. On pensait que seules les nutriments et l’oxygène passaient, et que les médicaments restaient “du côté de la mère”. Cette erreur fondamentale a conduit à une confiance aveugle dans la prescription de sédatifs aux femmes enceintes.

La résistance des rongeurs : Les premiers tests sur animaux ont été faits principalement sur des rats et des souris. Or, il s’est avéré plus tard que ces rongeurs sont naturellement résistants aux effets tératogènes de la thalidomide, car ils possèdent des taux d’antioxydants plus élevés protégeant leur embryon. Si les tests avaient été effectués sur des lapins ou des primates (ce qui est devenu la norme après la catastrophe), les malformations auraient été détectées immédiatement.

Cette tragédie a donné naissance aux essais cliniques modernes et à l’amendement Kefauver-Harris (1962), imposant la preuve de l’efficacité et de la sécurité (y compris reproductive) avant toute mise sur le marché.

Tous les acides aminés présents dans le vivant correspondent à l'énantiomère gauche (S) !

$\Rightarrow$ Le vivant est homochiral :
il n'utilise qu'une seule "main".

Inverser un seul acide aminé dans une protéine (en passant de S à R) empêcherait le bon repliement de la protéine et lui ferait perdre sa fonction biologique.

À l'inverse, les sucres de notre ADN et
de notre ARN sont tous de forme "droite".

Un léger surplus de forme S a été
observé sur une météorite

Une hypothèse serait que la lumière circulairement polarisée émise par des étoiles massives dans le nuage pré-solaire aurait détruit préférentiellement les formes R, laissant un surplus de formes S qui auraient ensuite "ensemencé" la Terre.

Solution tampon

Solution pour laquelle un ajout modéré
d’acide ou de base modifie peu le pH.

De même, le pH varie peu lors d'une dilution.

Une telle solution peut exister grâce à l’"effet tampon" qui consiste en l’absorption ou la libération d’ion hydrogène par les espèces présentes dans la solution.

On rencontre cet effet dès lors qu'un acide $\color{#FF968D}\ce{AH}$
et sa base conjuguée $\color{#56C1FF}\ce{A-}$ sont présents en solution.

Si pour une raison quelconque, la concentration en ions oxonium varie en solution, cela va déplacer
l’équilibre entre $\color{#FF968D}\ce{AH}$ et $\color{#56C1FF}\ce{A-}$ de manière
à compenser cette variation.

Cette compensation (et donc l'effet tampon)
est maximale quand ${\color{#FF968D}\ce{[AH]}}={\color{#56C1FF}\ce{[A-]}}$,
c'est-à-dire lorsque $\mathrm{pH}=$ $\mathrm{pK_A}$.

Les courbes de titrage pH-métrique confirment que les plus faibles variations de pH ont lieu dans cette zone :

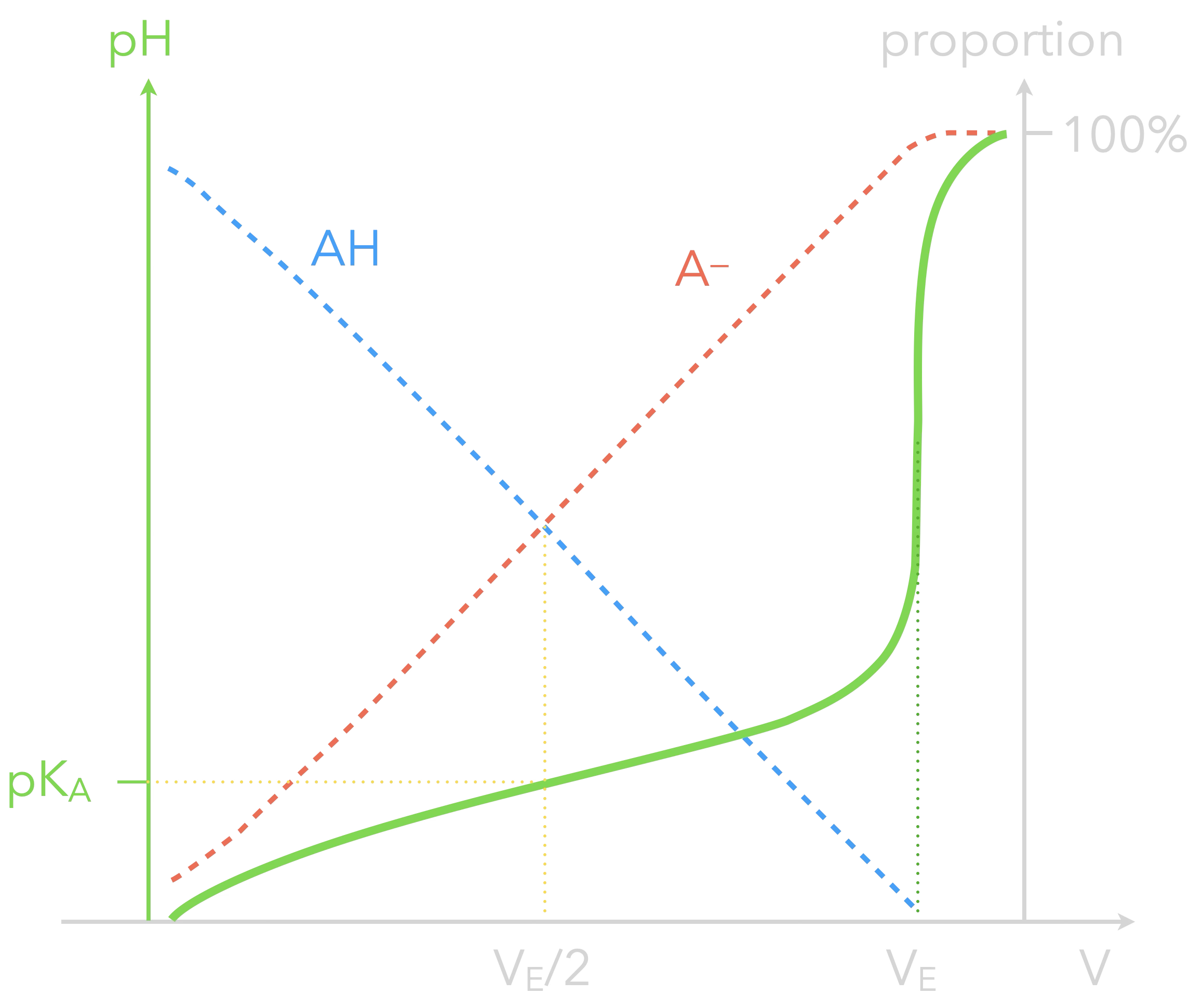
Le sang est une solution tampon !

C’est le couple acide carbonique $\ce{H2CO3}$ /
ion bicarbonate (ou hydrogénocarbonate) $\ce{HCO3-}$
qui est le principal responsable du maintien du pH
du sang entre 7,35 et 7,45.

Au-delà de la petite fenêtre, des acidoses ou alcaloses se développent rapidement et conduisent à la mort.

💀

La forme ampholyte des acides aminés
renforce aussi l'effet tampon :

un excès d'ions $\ce{H+}$ peut être absorbé par le groupe $\ce{-COO^-}$ qui peut en absorber ;
un déficit de $\ce{H+}$ peut être compensé par le groupe $\ce{-NH3^+}$ qui peut en libérer.

Application

retour sur l’exercice du chaulage du lac acide

Pourquoi utilise-t-on du carbonate de calcium
sachant que l’ion carbonate est une base faible
(couple $(\ce{HCO3-}/\ce{CO3^2-}$) de $\mathrm{p}K_\mathrm{A}=10,3$)
plutôt qu’une base forte comme
l’hydroxyde de sodium ?

Un titrage pH-métrique d’un litre de solution à pH 5,5 représentant l’eau du lac est réalisé avec une solution d’ions carbonates avec $\ce{[CO3^2-]=\pu{1,00 mmol*L-1}}$, puis par une solution d’ions hydroxyde avec $\ce{[HO^-]=\pu{1,00 mmol*L-1}}$.

La concentration de ces solutions
titrantes est-elle adaptée ?

Graphes de l’activité Python
“Taux d’avancement et $\mathrm{p}K_A$”

Retour site

Force des acideset des bases