Lunette astronomique
Rappels sur les lentilles
Par quoi est caractérisée une lentille convergente ?

Par sa distance focale $f’=\overline{OF’}$
F’ est le foyer image de la lentille
et O son centre optique.
Foyer objet F tel que $\overline{\mathrm{OF}}=-\overline{\mathrm{OF’}}=-f'$
Quelle est la caractéristique géométrique des rayons émis par un objet (source) très éloigné ?
Ils sont parallèles.
Que deviennent ces rayons émis par une source
très éloignée lorsqu’ils traversent la lentille ?
Ils convergent en un point du plan focal image.
Comment trouver ce point ?
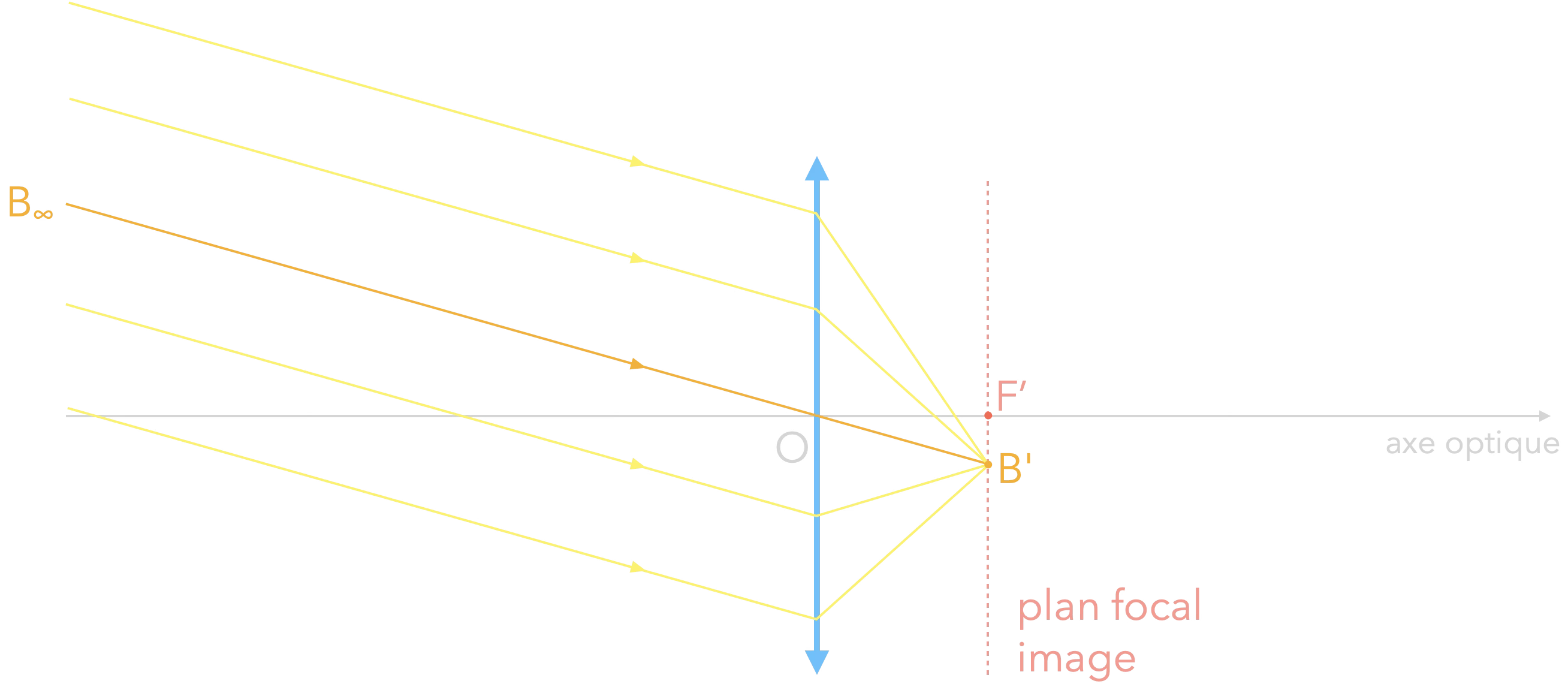
C'est le point d'intersection entre le plan focal et le rayon particulier passant pas O (seul rayon non dévié).
Et si l’objet est dans la direction de l’axe optique ?
Les rayons convergent au foyer image F'.
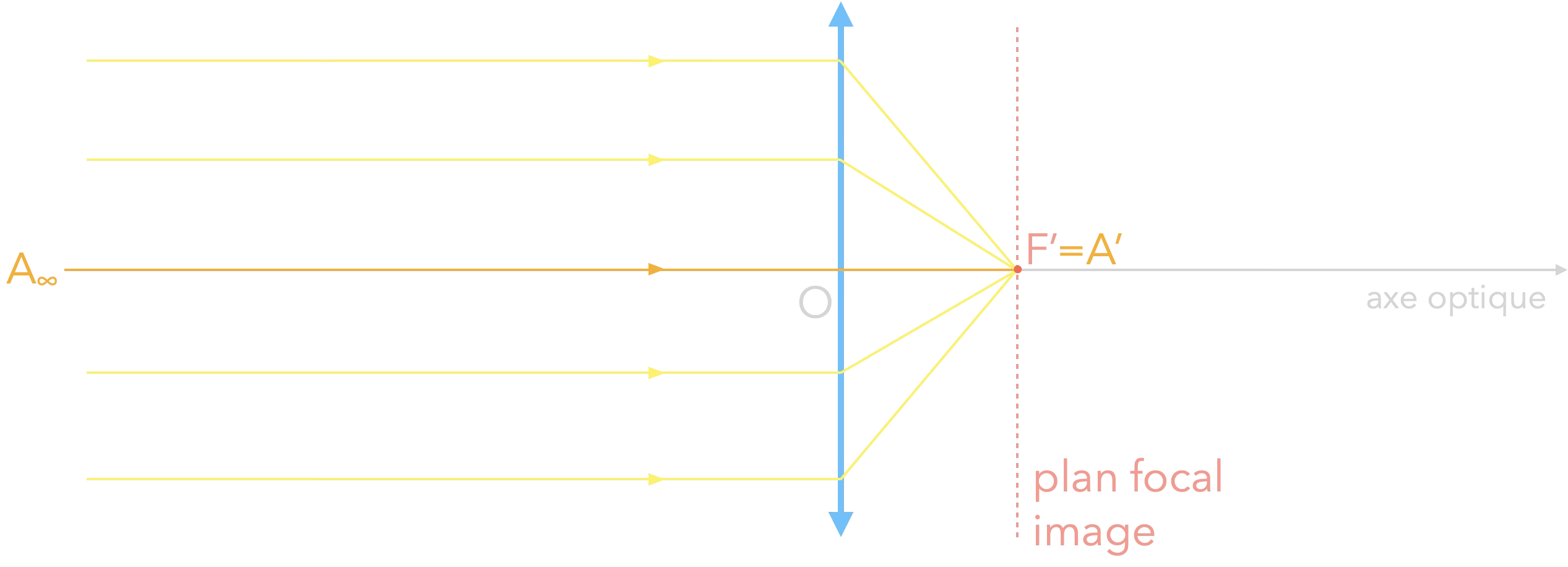
$$-\infty \xrightarrow{(L)} \mathrm{F'}$$
Où doit être placé l’objet pour que la lentille en fasse une image en $+\infty$ ($\Leftrightarrow$ rayons émergents parallèles) ?
Sur le plan focal objet.
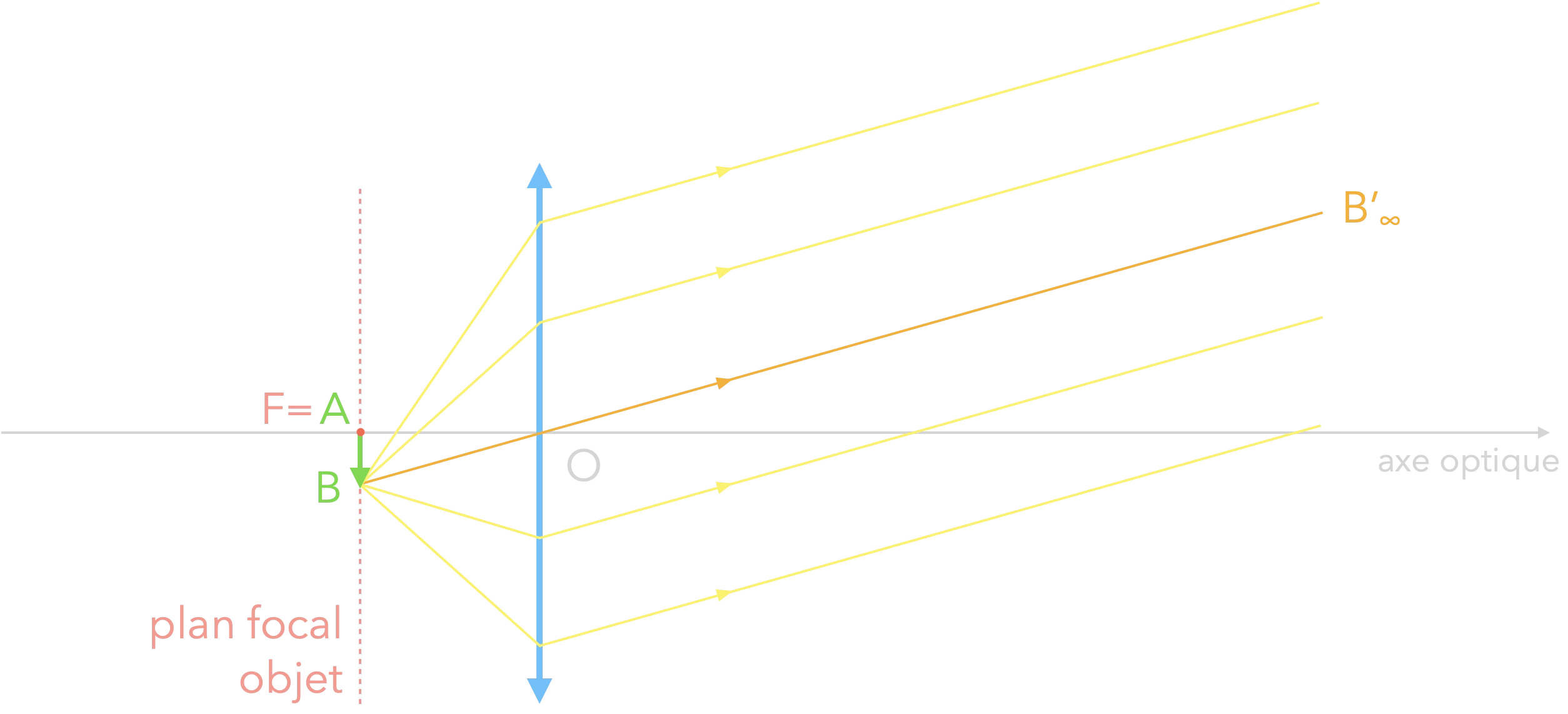
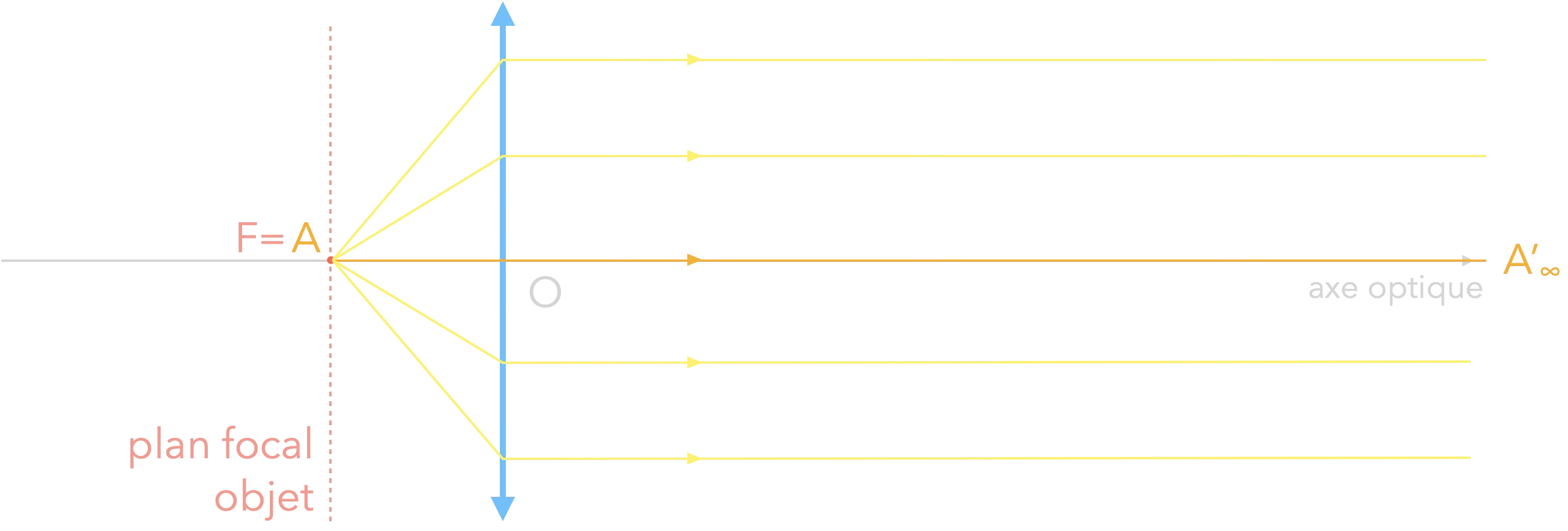
$$F \xrightarrow{(L)} +\infty$$
Où doit-être l’objet pour que nos yeux
puissent le voir sans accommoder ?
Très loin (par rapport à la distance focale
de nos yeux), c'est-à-dire en $-\infty$.
La lunette afocale
Beaucoup d’instruments d’optique (lunette astronomique, télescope, microscope, etc.) se terminent par une lentille appelée oculaire.
Le rôle de l'oculaire est d'envoyer
les rayons dans l'œil.
Comment doivent être ces rayons dans l’idéal ?
Parallèles entre eux !
Et comme une lunette astronomique regarde des objets très loins, les rayons issus d’un point objet arrivent eux aussi parallèles entre eux.

Une lunette astronomique bien réglée est alors
par définition afocale puisqu’on a :
$$-\infty \xrightarrow{\text{(lunette astronomique)}} + \infty$$
L'image d'un objet à l'infini est située à l'infini.
À quoi sert une lunette astronomique ?
Elle permet de "grossir" des objets très éloignés.
Mais que veut dire “grossir” ?
Grossir, c'est augmenter le diamètre apparent de l'objet, c'est-à-dire l'angle (⚠️) sous lequel l'objet est vu.
Supposons que l’objet soit vu sous l’angle $\alpha$ sans la lunette (le diamètre apparent de l’objet vaut donc $\alpha$)
et sous l'angle $\alpha'$ à travers la lunette.
Le bas de l’objet est aligné avec l’axe optique et le rayon issu du haut de l’objet fait un angle $\alpha$ avec l’axe optique.
Le rayon issu du haut de l'objet fait l'angle $\alpha'$
avec l'axe optique en quittant la lunette.
Le grossissement $G$ est alors défini par :
On utilise deux lentilles convergentes
pour réaliser une lunette astronomique de type Kepler.
La première est l'objectif et la seconde,
déjà évoquée, est l'oculaire.
Comment disposer les deux lentilles pour que l’oculaire renvoie les rayons le traversant parallèlement ?
Conclusion
$$ {\color{#56C1FF}F’_{\mathrm{ob}}} = {\color{#FF95CA}F_{\mathrm{oc}} } $$
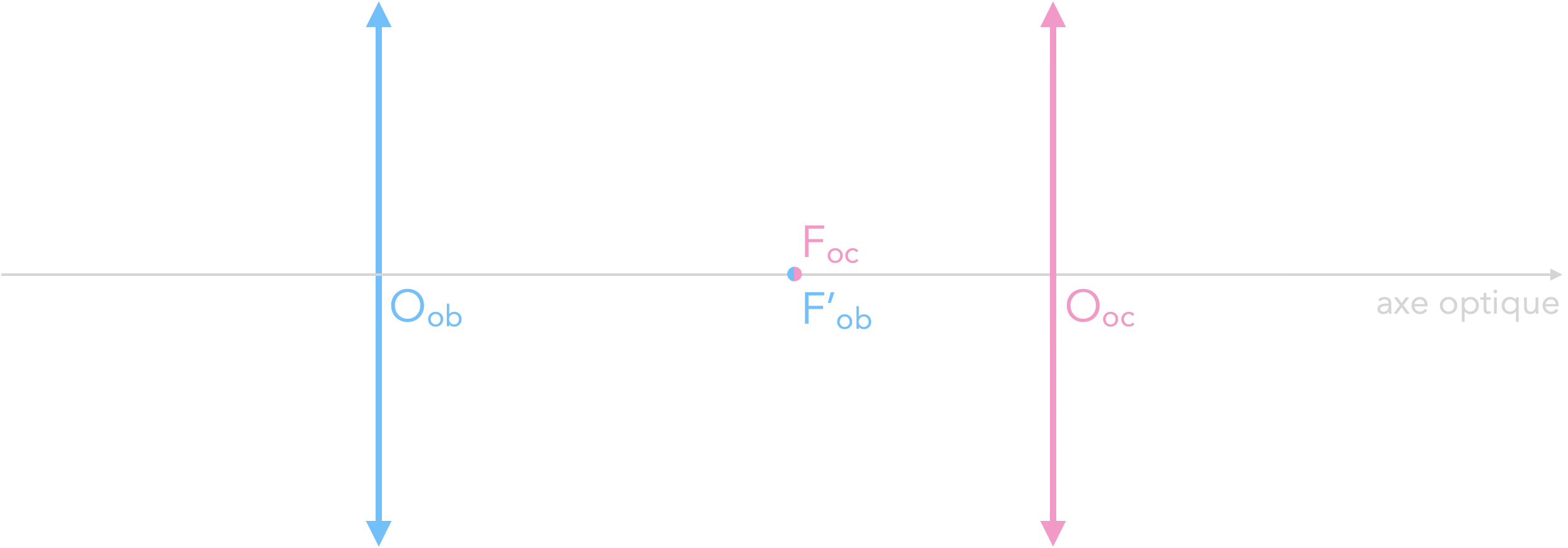
Le foyer image de l'objectif doit être
confondu avec le foyer objet de l'oculaire
pour obtenir une lunette afocale.
Conséquence :
La distance $\mathrm{O_{ob} O_{oc}}$ entre les deux lentilles
(qui correspond approximativement à
la longueur de la lunette) vaut $f'_\mathrm{ob}+f'_\mathrm{oc}$.
Comment exprimer le grossissement
en fonction de $f’_{ob}$ et $f’_{oc}$ ?
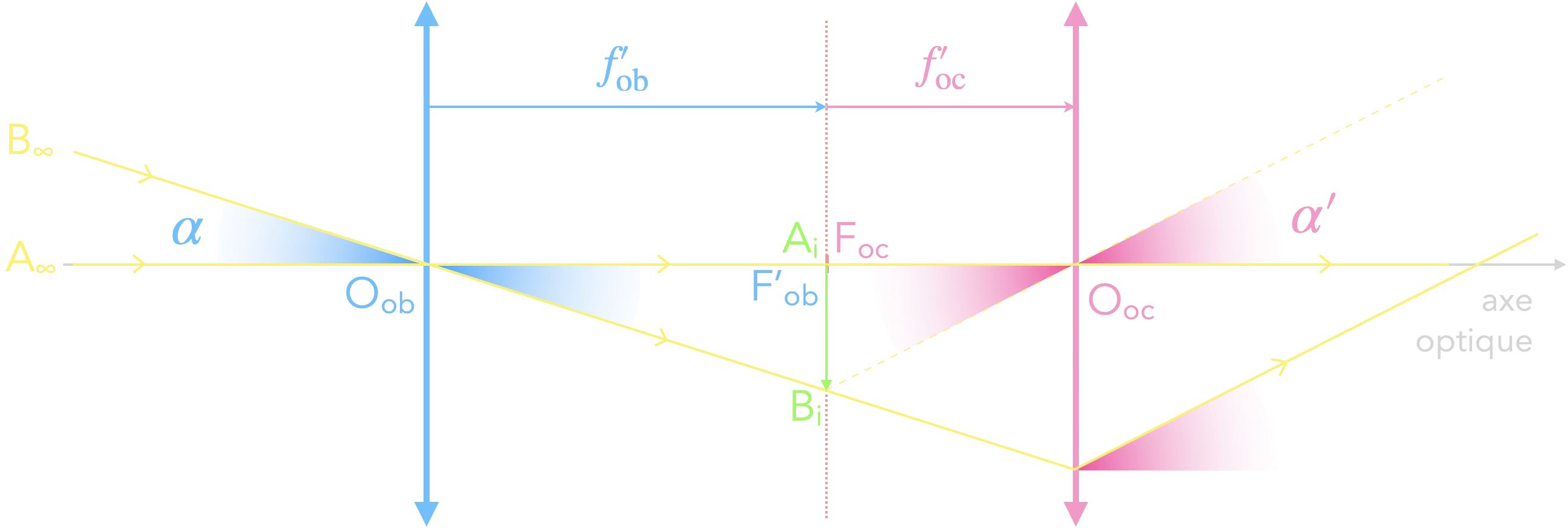
Rq : $\color{#88FA4E}\mathrm{A_i B_i}$ est l’image réelle renversée
de l’objet lointain $\color{#FFF056}\mathrm{A_\infty B_\infty}$ par l’objectif.
Sur le triangle $\mathrm{O_{ob}A_i B_i}$ :
$\mathrm{A_i B_i}=f'_\mathrm{ob}\times\tan(\alpha)$
Sur le triangle $\mathrm{O_{oc}A_i B_i}$ :
$\mathrm{A_i B_i}=f'_\mathrm{oc}\times\tan(\alpha')$
D'où :
$f'_\mathrm{ob}\times\tan(\alpha) = f'_\mathrm{oc}\times\tan(\alpha')$
$\displaystyle \Leftrightarrow \frac{\tan(\alpha')}{\tan(\alpha)} = \frac{f'_\mathrm{ob}}{f'_\mathrm{oc}}$
Et si on se place dans l'approximation des petits angles
($\alpha,\alpha'\ll \pu{1 rad}$), on a
$\tan(\alpha)\approx \alpha$
et $\tan(\alpha')\approx\alpha'$ ($\alpha$ et $\alpha'$en radians)
On en déduit :
⚠️ À savoir redémontrer ⚠️
À quelle condition sur $f’_\mathrm{ob}$ et $f’_\mathrm{oc}$ a-t-on un grossissement supérieur à 1 ?
Schémas
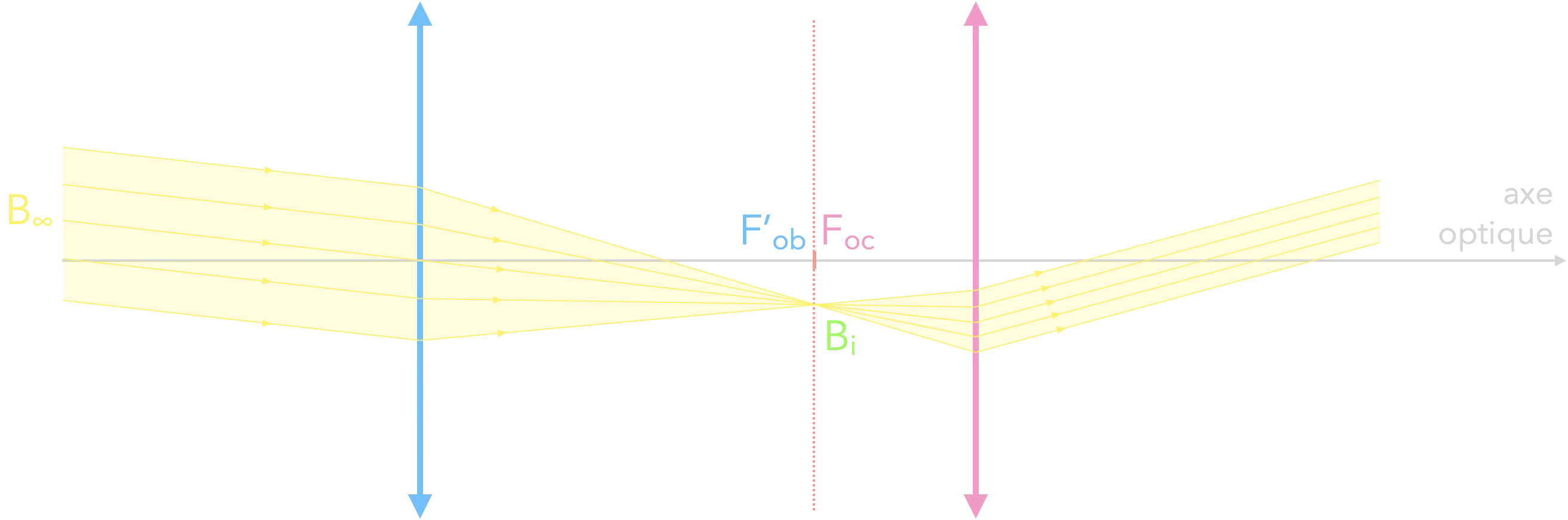
Qu’est-ce qui ne va pas dans ce schéma ?
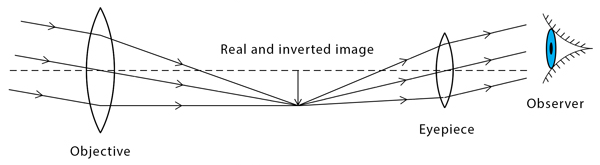
Les rayons ne doivent pas être déviés en Bi !

Avec œil :
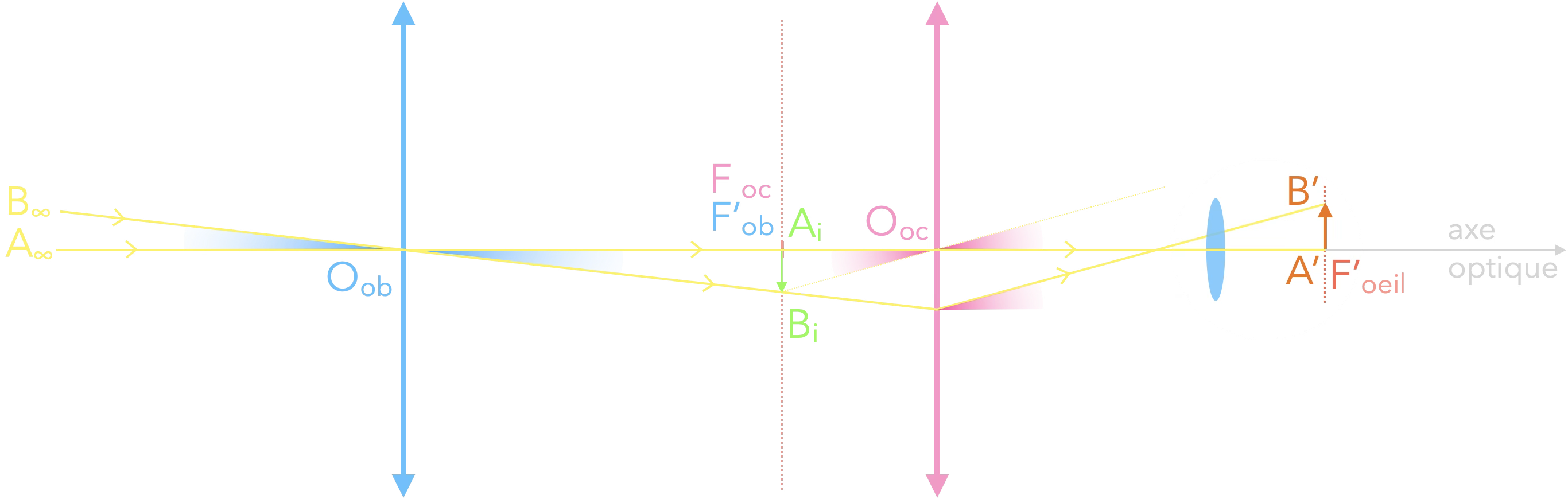
Faisceau issu de $\mathrm{B_\infty}$ :
Caractéristiques d’une
lunette astronomique
Les étoiles autres que le soleil sont trop loin pour
être vues autrement que comme des points
à travers une lunette astronomique.
Quelle autre utilité peut avoir la lunette ?
La lunette permet d’augmenter la luminosité en concentrant la lumière passant à travers l’objectif.
Pour cela, il faut que la lentille convergente servant d'objectif ait le plus grand diamètre possible.
Mais les grandes lentilles présentent
de nombreux problèmes :
- Une lentille disperse
$\rightarrow$ problème d'aberration chromatique. - Une grande lentille est très lourde et peut fléchir.
- L'obtention d'un verre homogène et son polissage sont difficiles et longs. Les coûts deviennent prohibitifs.
Les miroirs gomment tous ces défauts.
C'est pour cela que les grands télescopes
sont réflecteurs et non réfracteurs.
En pratique, on n'est pas allé au-delà de 1 m pour l'objectif d'une lunette alors qu'il existe (presque)
des télescope de 40 m de diamètre.
- Rôle de l'objectif :
il collecte la lumière et forme l'image intermédiaire $\mathrm{A_i B_i}$ de l'objet situé à l'infini. - Rôle de l'oculaire : il sert de loupe en formant l'image de $\mathrm{A_i B_i}$ en l'infini.
Pour avoir la meilleure
lunette astronomique, il faut donc :
- une lentille de grand diamètre pour l'objectif afin d'avoir le meilleur collecteur de lumière possible,
- une distance focale de l'objectif grande par rapport
à celle de l'oculaire pour avoir le plus grand grossissement possible.
L'encombrement de la lunette est alors approximativement donné par la somme des
distances focales de l'oculaire et de l'objectif.