Cinématique
La cinématique est l’étude du mouvement.
Un mouvement s’étudie dans un référentiel.
la position ou le mouvement.
Un référentiel est composé :
- d'un repère d'espace $(0;\vec{i},\vec{j},\vec{k})$
permettant de définir la position, - d'un repère de temps ou horloge $(t)$
permettant d'associer une date à chaque position.
Référentiels usuels :
- Référentiel terrestre :
tout solide immobile à la surface de la Terre.
- Référentiel géocentrique :
solide défini par le centre de la Terre et 3 étoiles lointaines considérées comme fixes.
- Référentiel héliocentrique :
solide défini par le centre du Soleil et 3 étoiles lointaines considérées comme fixes.
Vecteur position
Dans un repère orthonormé $(0;\vec{i},\vec{j},\vec{k})$, la position d’un point $\mathrm{M}$ à la date $t$ est donnée par son vecteur position
$\overrightarrow{\mathrm{OM}}(t)\left(\begin{aligned}x(t)\\y(t)\\z(t)\end{aligned}\right)$
$\overrightarrow{\mathrm{OM}}(t)=x(t)\vec{i}+y(t)\vec{j}+z(t)\vec{k}$
On notera fréquemment :
$$ \begin{cases} x(t)=\ldots\\ y(t)=\ldots\\ z(t)=\ldots \end{cases} $$Rq : en pratique, les mouvements seront presque toujours à 2 dimensions seulement. $$ \begin{cases} x(t)=\ldots\\ y(t)=\ldots \end{cases} $$
La norme $\mathrm{OM}$(t) du vecteur position vaut :
$\mathrm{OM}(t)=||\overrightarrow{\mathrm{OM}}(t)||=\sqrt{x(t)^2+y(t)^2+z(t)^2}$
Unité : $\pu{m}$
Vecteur vitesse
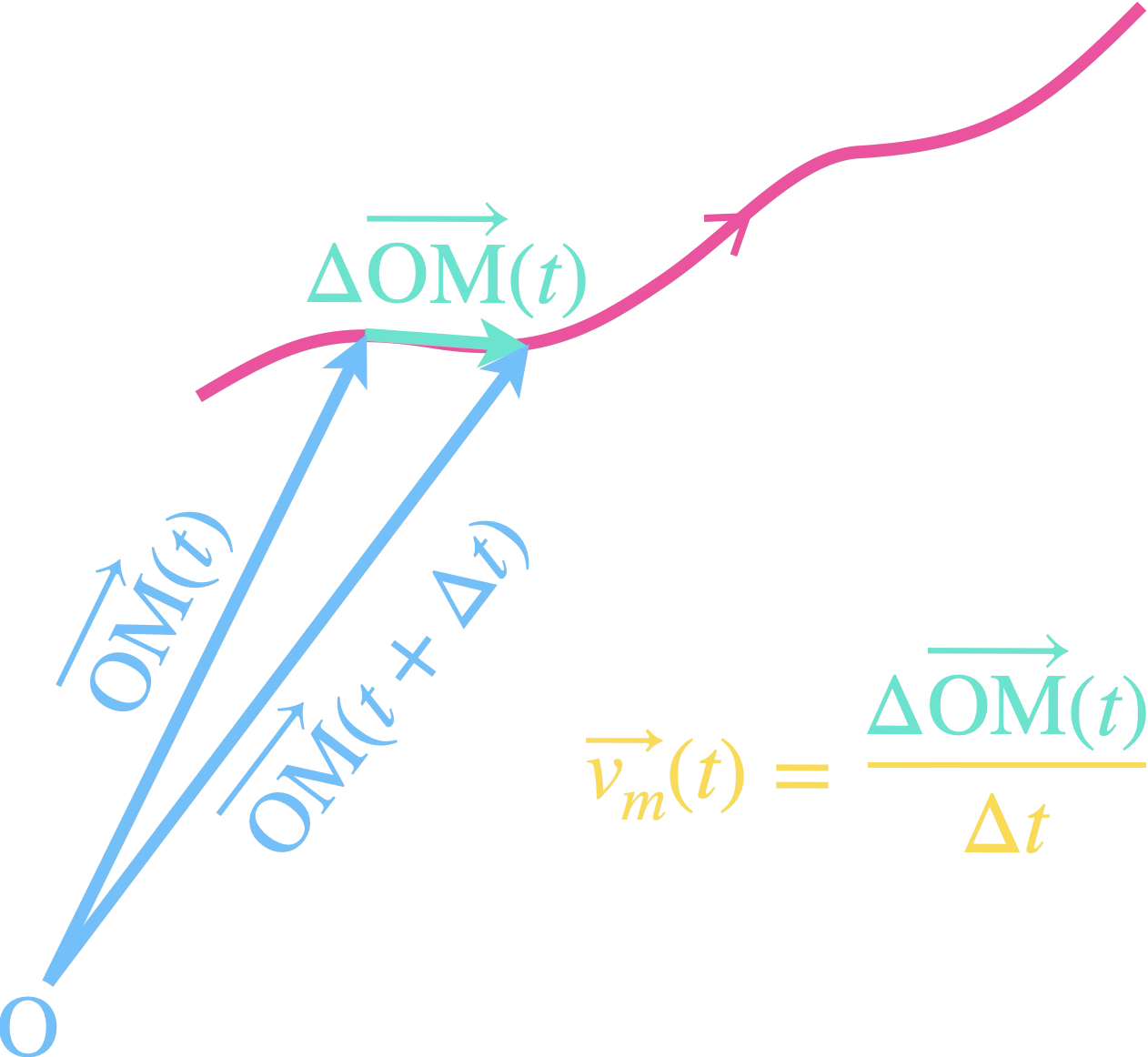
Le vecteur vitesse moyenne d’un point $\mathrm{M}$
entre deux instants $t$ et $t+\Delta t$ est défini par :
$ \begin{aligned} \vec{v}_m(t) &= \frac{\overrightarrow{\mathrm{M}(t)\mathrm{M}(t+\Delta t)}}{\Delta t}\\ &= \frac{\overrightarrow{\mathrm{OM}(t+\Delta t)}-\overrightarrow{\mathrm{OM}(t)}}{\Delta t}\\ &=\frac{\overrightarrow{\Delta\mathrm{OM}(t)}}{\mathrm{\Delta}t} \end{aligned} $
On obtient le vecteur vitesse $\vec{v}(t)$
en faisant tendre $\Delta$ vers $0$.
On obtient alors la dérivée du vecteur position.
Le vecteur vitesse $\vec{v}(t)$ d’un point $\mathrm{M}$ à la date $t$ est la dérivée par rapport au temps du vecteur position :
Notation :
En physique, $\Delta$ correspond à une variation
et $\mathrm{d}$ à une variation infinitésimale.
$$ \begin{array}{rcrcrcr} \vec{v}(t) & = & v_x(t)\, \vec{i} & + & v_y(t) \, \vec{j} & + &v_z(t) \, \vec{k}\\ & = &\frac{\mathrm{d}x}{\mathrm{d}t} \,\vec{i} & +& \frac{\mathrm{d}y}{\mathrm{d}t} \, \vec{j} & + &\frac{\mathrm{d}z}{\mathrm{d}t} \, \vec{k} \end{array} $$
$$ \begin{cases} v_x(t)=\frac{\mathrm{d}x}{\mathrm{d}t}=\ldots\\ v_y(t)=\frac{\mathrm{d}y}{\mathrm{d}t}=\ldots\\ v_z(t)=\frac{\mathrm{d}z}{\mathrm{d}t}=\ldots \end{cases} $$
Rq :
La notation physique $\frac{\mathrm{d}x}{\mathrm{d}t}$ correspond
à la notation mathématique $x'(t)$.

Le vecteur vitesse est porté par la tangente à la trajectoire et orienté dans le sens du mouvement.
La norme $v$(t) du vecteur vitesse vaut :
$v(t)=||\vec{v}(t)||=\sqrt{v_x(t)^2+v_y(t)^2+v_z(t)^2}$
Unité : $\pu{m*s-1}$
Vecteur accélération
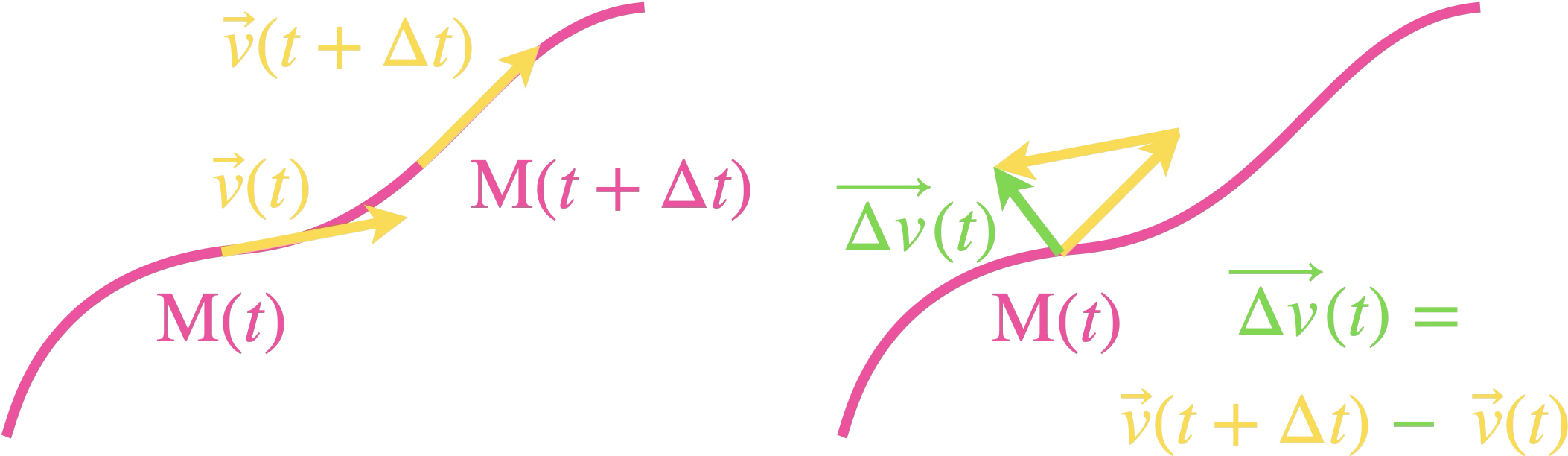
Le vecteur accélération moyenne d’un point $\mathrm{M}$
entre deux instants $t$ et $t+\Delta t$ est défini
à partir du vecteur variation de vitesse :
$ \begin{aligned} \vec{a}_m(t) &= \frac{\vec{v}(t+\Delta t)-\vec{v}(t)}{\Delta t}\\ &= \frac{\overrightarrow{\Delta v}(t)}{\Delta t} \end{aligned} $
On obtient le vecteur vitesse $\vec{a}(t)$
en faisant tendre $\Delta$ vers $0$.
Cela donne la dérivée du vecteur vitesse et donc
la dérivée seconde du vecteur position.
Le vecteur accélération $\vec{a}(t)$ d’un point $\mathrm{M}$ à la date $t$ est la dérivée par rapport au temps du vecteur vitesse et la dérivée seconde du vecteur position :
$$ \begin{array}{rcrcrcr} \vec{a}(t) & = & a_x(t)\, \vec{i} & + & a_y(t) \, \vec{j} & + &a_z(t) \, \vec{k}\\ & = &\frac{\mathrm{d}v_x}{\mathrm{d}t} \,\vec{i} & +& \frac{\mathrm{d}v_y}{\mathrm{d}t} \, \vec{j} & + &\frac{\mathrm{d}v_z}{\mathrm{d}t} \, \vec{k} \end{array} $$
$$ \begin{cases} a_x(t)=\frac{\mathrm{d}v_x}{\mathrm{d}t}=\ldots\\ a_y(t)=\frac{\mathrm{d}v_y}{\mathrm{d}t}=\ldots\\ a_z(t)=\frac{\mathrm{d}v_z}{\mathrm{d}t}=\ldots \end{cases} $$

Le vecteur accélération est dans la direction
et le sens du vecteur variation de vitesse.
Dans le cas d'une trajectoire courbe,
il pointe vers l'intérieur de la courbe.
La norme $a$(t) du vecteur accélération vaut :
$a(t)=||\vec{a}(t)||=\sqrt{a_x(t)^2+a_y(t)^2+a_z(t)^2}$
Unité : $\pu{m*s-2}$
Vidéos
Jusqu’à 3'22’’ (la méthode d’Euler est introduite après, utile pour le supérieur mais pas au programme de Tspé)
Jusqu’à 4'51’’ (mouvement circulaire uniforme décrit dans un repère orthonormé fixe = pas au programme)
Mouvements rectilignes
Un mouvement est rectiligne
si sa trajectoire est une droite.

Le vecteur vitesse conserve alors
la même direction (celle du mouvement).
Si le vecteur vitesse est constant,
le mouvement est dit rectiligne uniforme.
Que vaut alors le vecteur accélération ?
$$ \vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=\vec{0} $$
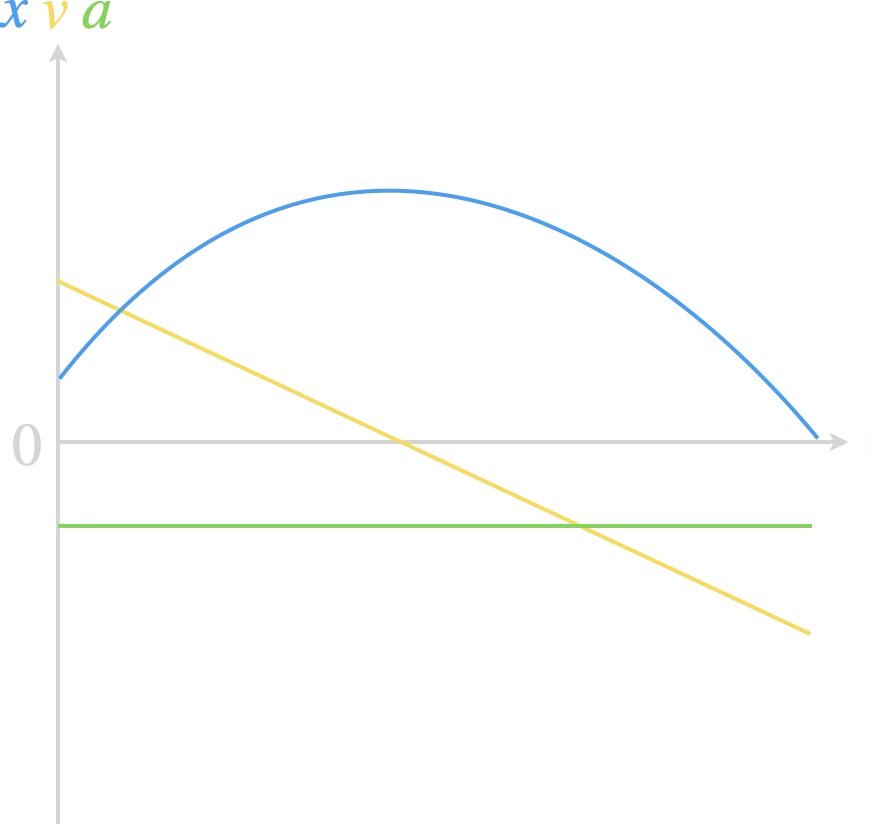
Tracer les évolutions de la position $x(t)$,
de la vitesse $v(t)$ et de l’accélération $a(t)$.

Tracer les évolutions de la position $x(t)$,
de la vitesse $v(t)$ et de l’accélération $a(t)$.
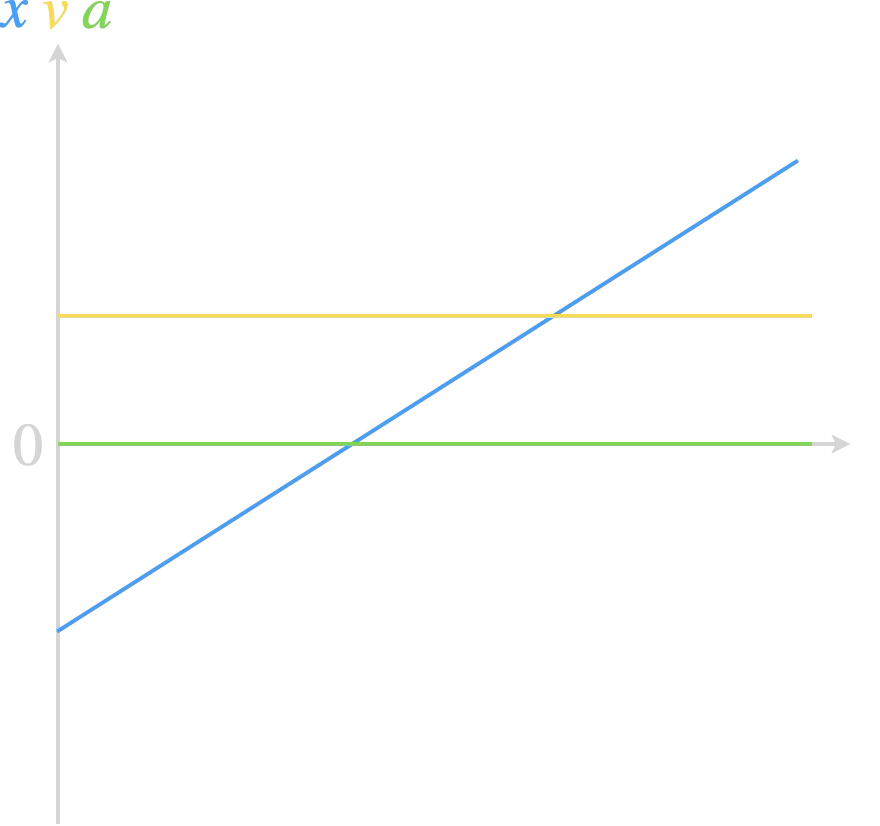
$\vec{a}(t)=\vec{cte}$
Un mouvement rectiligne avec un vecteur accélération constant est dit rectiligne uniformément accéléré.
Tracer les évolutions de la position $x(t)$,
de la vitesse $v(t)$ et de l’accélération $a(t)$.

Tracer les évolutions de la position $x(t)$,
de la vitesse $v(t)$ et de l’accélération $a(t)$.
Petite exercice :

Avant d’aborder le virage des combes (5) du circuit
de Spa-Francorchamps, un pilote de F1 freine fortement pour passer sa vitesse de 327 km/h
à 176 km/h en 1,48 s.
En supposant le mouvement rectiligne uniformément accéléré, décrire le vecteur accélération de la F1.
Sur combien de mètres a lieu le freinage ?
Il se fait en réalité sur 93 m, que peut-on conclure ?
Mouvements circulaires
Un mouvement est circulaire
si sa trajectoire est un cercle (ou un arc de cercle).
On parle de mouvement circulaire uniforme si
la norme du vecteur vitesse est constante.
Pour décrire le mouvement circulaire
d’un point M sur un cercle de centre O,
on utilise un repère de Frenet.
C’est un repère mobile centré au point
étudié M et de vecteurs unitaires :
- $\vec{u}_T$ : vecteur tangent
$\hphantom{\vec{u_t}}$ tangent à la trajectoire,
$\hphantom{\vec{u_t}}$ orienté dans le sens du mouvement - $\vec{u}_N$ : vecteur normal
$\hphantom{\vec{u_n}}$ de direction (OM)
$\hphantom{\vec{u_n}}$ orienté vers le centre O
Rq : $\vec{u}_T$ est parfois noté $\vec{T}$ et $\vec{u}_N$ noté $\vec{N}$.
Dans le repère de Frenet $(\mathrm{M};\vec{u}_T,\vec{u}_N)$,
le vecteur vitesse se décompose en :
Finalement :
$\vec{v}(t)=v(t)\,\vec{u}_T$
Et le vecteur accélération :
Finalement :
$\vec{a}(t)=\frac{\mathrm{d}v}{\mathrm{d} t}\,\vec{u}_T + \frac{v^2}{R}\,\vec{u}_N$
Et si le mouvement est circulaire uniforme ?
On a $\frac{\mathrm{d}v}{\mathrm{d}t}=0$ puisque $v=\mathrm{cte}$
$$ \vec{a}(t) \begin{cases} a_T(t)=0\\ a_N(t)=\frac{v^2}{R} \end{cases} $$
L’accélération est centripète (dirigée
vers le centre) et de norme constante.