Transformations nucléaires
Diagramme (N,Z)
Rappel notation symbolique d’un élément :
- $\ce{X}$ est le symbole chimique de l'élément
- $\ce{\color{#FF968D}Z}$ est le nombre de protons du noyau.
- $\ce{\color{#56C1FF}A}$ est le nombre de nucléons du noyau.
Rq :
- $\ce{\color{#FF968D}Z}$ (le numéro atomique), permet de
déterminer la charge du noyau :
$Q=\ce{\color{#FF968D}Z}\times e$ - $\ce{\color{#56C1FF}A}$ (aussi appelé nombre de masse)
permet de déterminer approximativement
la masse du noyau :
$m\approx\ce{\color{#56C1FF}A}\times m$ (avec $m_p\approx m_n\approx m$)
Le nombre $\ce{N}$ de neutrons du noyau est donné par :
On appelle isotopes deux noyaux
ayant le même nombre de protons $\ce{\color{#FF968D}Z}$
mais un nombre différent de neutrons $\ce{\color{#FFF056}N}$.
(ou, ce qui revient au même,
un nombre différent de nucléons $\ce{\color{#56C1FF}A}$)
On désigne généralement un isotope
par son nom chimique suivi de son nombre $\ce{\color{#56C1FF}A}$.
Le carbone 14 ou l'uranium 235 par exemple.
On peut ranger tous les isotopes
connus dans un diagramme $\ce{(N,Z)}$
(avec $\ce{\color{#FF968D}Z}$ en abscisse et $\ce{\color{#FFF056}N}$ en ordonnée).
On constate que les noyaux stables
sont très minoritaires et se concentrent dans
une vallée de la stabilité (autour de $\ce{N=Z}$)
pour les petits noyaux puis avec $\ce{N>Z}$).
À partir du bismuth ($\ce{Z=83}$),
il n'y a plus d'isotopes stables.
Transformations nucléaires
Les noyaux instables subissent
des désintégrations radioactives
mettant en jeu une ou plusieurs
transformation(s) nucléaire(s) du noyau
visant à le rapprocher de la vallée de la stabilité.
Lois de conservations
Lors d'une transformation nucléaire, il y a
- conservation de la charge,
- conservation du nombre de nucléons,
Exemple :
Lorsqu’un noyau d’uranium 235 absorbe un neutron,
il peut fissioner en deux noyaux fils dont l’un est
le strontium 94 tout en émettant 2 neutrons.
Déterminer l'autre noyau fils.
Types de radioactivité
Lors d’une désintégration radioactive,
différentes transformations nucléaires peuvent permettre de rapprocher le noyau fils de la stabilité.
Historiquement, on a classé ces différents types de radioactivité en fonction du rayonnement émis :
α, β-, β+ et γ.
Radioactivité alpha $\alpha$
Exemple :
$$\ce{^{238}_{92} U -> ^{234}_{90} Th +\color{#FF968D} \alpha}$$
Par conservation de la charge et du nombre de nucléons, déterminer la nature des rayons alpha.
La radioactivité alpha correspond à l’émission
de noyaux d’Hélium $\ce{^4_2He}$ (particule α).
Radioactivité bêta moins $\beta^-$
Exemple :
$$\ce{^{14}_{6} C -> ^{14}_{7} N + \color{#56C1FF}\beta^-} + \; ^0_0\bar{\nu_e}$$
Par conservation de la charge et du nombre de nucléons, déterminer la nature des rayons $\beta^-$.
La radioactivité $\beta^-$ correspond à
la transformation d’un neutron en proton
en émettant un électron $^{\;\; 0}_{-1}e$ (particule $\beta^-$).
Elle concerne des noyaux
comportant trop de neutrons.
Radioactivité bêta plus $\beta^+$
Exemple :
$$\ce{^{18}_{9} F -> ^{18}_{8} O + \color{#FF95CA}{\beta^+} + \; ^0_0\nu_e }$$
Par conservation de la charge et du nombre de nucléons, déterminer la nature des rayons $\beta^+$.
La radioactivité $\beta^+$ correspond à
la transformation d’un proton en neutron
en émettant un positron $^{\;\; 0}_{+1}e$
(antiparticule de l’électron).
Elle concerne des noyaux
comportant trop de protons.
Radioactivité gamma $\gamma$
Exemple :
$$\ce{^{60}_{28} Ni^* -> ^{60}_{28} Ni + \color{#FFF056}\gamma}$$
Par conservation de la charge et du nombre de nucléons, déterminer la nature des rayons gamma.
La radioactivité gamma correspond à la désexcitation d’un noyau en émettant un photon (généralement dans le domaine électromagnétique des rayons gamma).
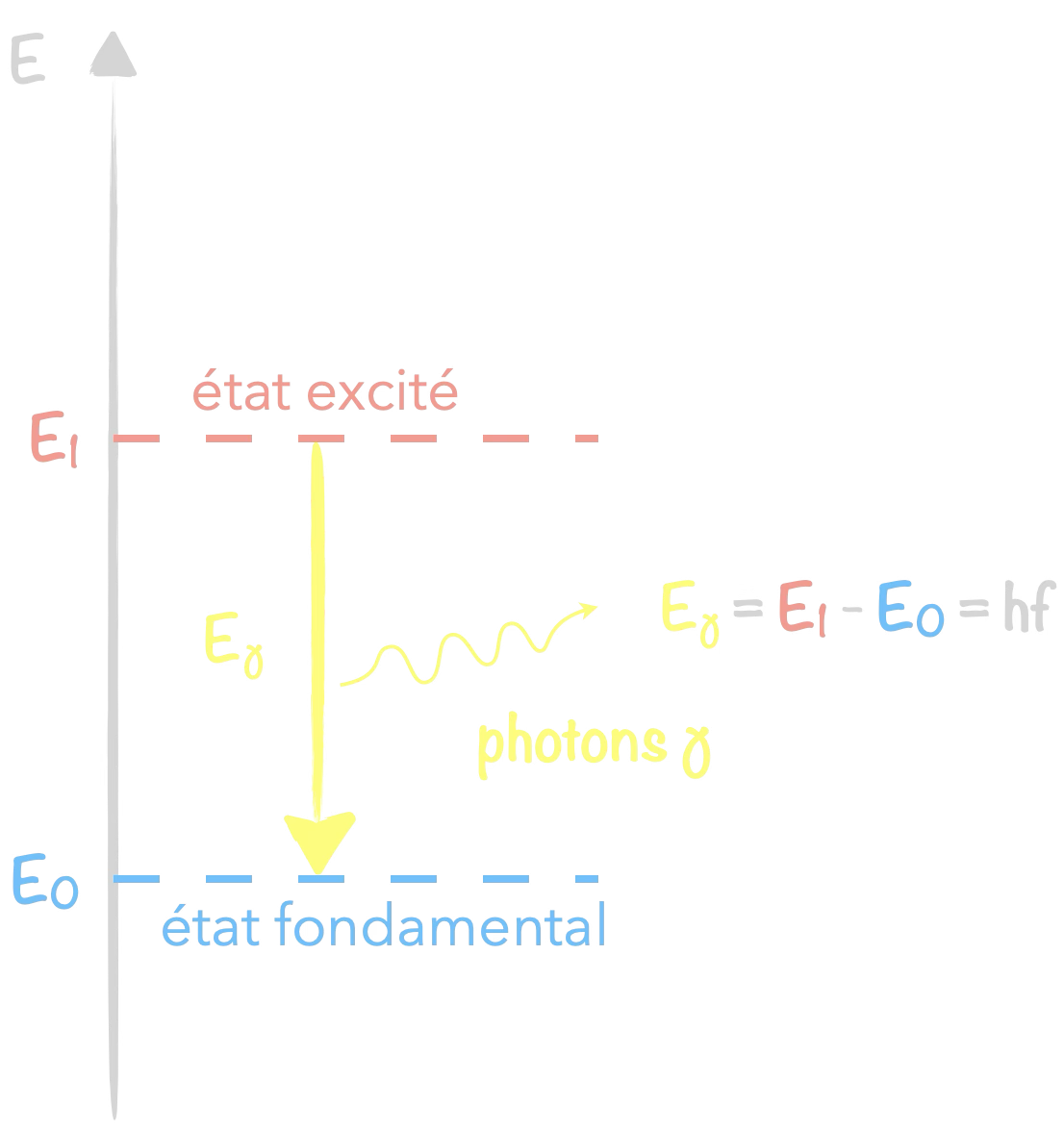
L’énergie est typiquement de l’ordre du MeV
($\approx\pu{1E-13 J}$)
Loi de décroissance radioactive
Un noyau radioactif a une certaine probabilité $\lambda \mathrm{d}t$
de se désintégrer pendant le prochain
petit laps de temps $\mathrm{d} t$ (avec $\mathrm{d} t \ll 1/\lambda$).
$\lambda$ (en $\pu{s^-1})$ est la constante radioactive.
Elle est indépendante du temps !
Après 1 s ou 1000 ans, la probabilité
pour un noyau de se désintégrer
pendant les prochains $\mathrm{d} t$
vaut toujours $\lambda\mathrm{d} t$.
Tous les mêmes isotopes ont
la même constante radioactive $\lambda$
et donc la même probabilité de se désintégrer
pendant le prochain laps de temps infinitésimal $\mathrm{d} t$.
La désintégration d'un noyau radioactif est donc
un phénomène aléatoire et l'évolution d'une population de noyau suit une loi statistique.
Soit $N(t)$ la population de noyaux non désintégrés
à un instant $t$. La variation $\mathrm{d} N$ de la population pendant le laps de temps infinitésimal $\mathrm{d} t$ vaut :
Qu'on peut réécrire :
On reconnaît une équation différentielle linéaire homogène du premier ordre à coefficient constant.
Les solutions sont de la forme :
Or si on connaît la population à l’instant initial :
On en déduit $C$ :
D’où la loi de décroissance radioactive :
- $N$ sans unité
- $t$ en $\pu{s}$ (ou l'inverse de l'unité de $\lambda)$
Rq :
On peut aussi écrire :
où $\tau=1/\lambda$ est le temps de vie moyen d'un noyau.
Activité
L’activité $A$ d’un échantillon radioactif est l’opposée
de la dérivée temporelle du nombre de noyaux :
- $A$ en becquerel (Bq)
On déduit $A(t)$ de la loi de décroissance radioactive :
${\color{#FF968D}{A_0 = \lambda N_0}} = A(t=0)$ est l'activité initiale.
Temps de demi-vie
On peut obtenir $t_{1/2}$ graphiquement
ou à partir de $\lambda$ (ou $\tau$) :
Population restante au bout de n demi-vies ?