Piles

Rappels oxydoréduction

Une réaction d'oxydo-réduction modélise
une transformation mettant en jeu
un transfert d'électrons entre
deux couples oxydant-réducteur.

L’oxydant d’un premier couple oxyde
le réducteur d’un deuxième couple.







On peut décomposer cette réaction
en deux demi-équations électroniques :


  • la réduction de l'oxydant 1.
  • l'oxydation du réducteur 2.
  • Lors d'une réduction, un oxydant est réduit :
    il capte des électrons et devient son réducteur conjugué.
    • $$\ce{Ox_1 + m e- = Red_1}$$
  • Lors d'une oxydation, un réducteur est oxydé :
    il cède des électrons et devient son oxydant conjugué. $$\ce{Red_2 = Ox_2 + n e-}$$

Pour obtenir l’équation bilan il faut équilibrer
le nombre d’électrons dans chaque demi-équation
afin qu’ils puissent disparaître du bilan.

Il y a en effet forcément autant d'électrons perdus
par les uns que d'électrons gagnés par les autres.

$$\quad\qquad\ce{Ox_1} + \color{#FFF056}\ce{m e-}\color{#93a1a1}=\ce{Red_1}\qquad\qquad \color{#56C1FF}(\times n)\qquad$$

$$\qquad\qquad\ce{Red_2 = Ox_2} + \color{#56C1FF} \ce{n e-}\quad \color{#FFF056} (\times m)$$

$$\ce{n Ox_1 + m Red_2 -> n Red_1 + m Ox_2}$$

Établir une équation d’oxydoréduction

🐣
Réaction d’oxydoréduction
entre l’ion fer II et l’ion cuivre II

Les couples sont :

$\left(\ce{Fe^3+(aq) / Fe^2+(aq)}\right)$
et $\left(\ce{Cu^2+(aq) / Cu (s)}\right)$

🐥
Réaction d’oxydoréduction
entre l’aluminium et le diiode

Les couples sont :

$\left(\ce{Al^3+(aq) / Al (s)}\right)$
et $\left(\ce{I2(aq) / I-(aq)}\right)$

🐥
Réaction d’oxydoréduction
entre le dioxygène et le zinc

Les couples sont :

$\left(\ce{O2(aq) / H2O (\ell)}\right)$
et $\left(\ce{Zn^2+(aq) / Zn (s)}\right)$

🐓
Réaction d’oxydoréduction entre
le dioxyde de soufre et l’ion permanganate

Les couples sont :

$\left(\ce{SO4^2-(aq) / SO2 (aq)}\right)$
et $\left(\ce{MnO4-(aq) / Mn^2+(aq)}\right)$

Pensez à simplifier à la fin.

🦚
Réaction d’oxydoréduction entre
l’éthanol et les ions dichromates.

Les couples sont :

$\left(\ce{Cr2O7^2- (aq)/ Cr^3+ (aq)}\right)$
et $\left(\ce{CH3COOH (\ell)/ CH3CH2OH (\ell)}\right)$

oxydants et réducteurs usuels

Parmi les oxydants, on peut citer :


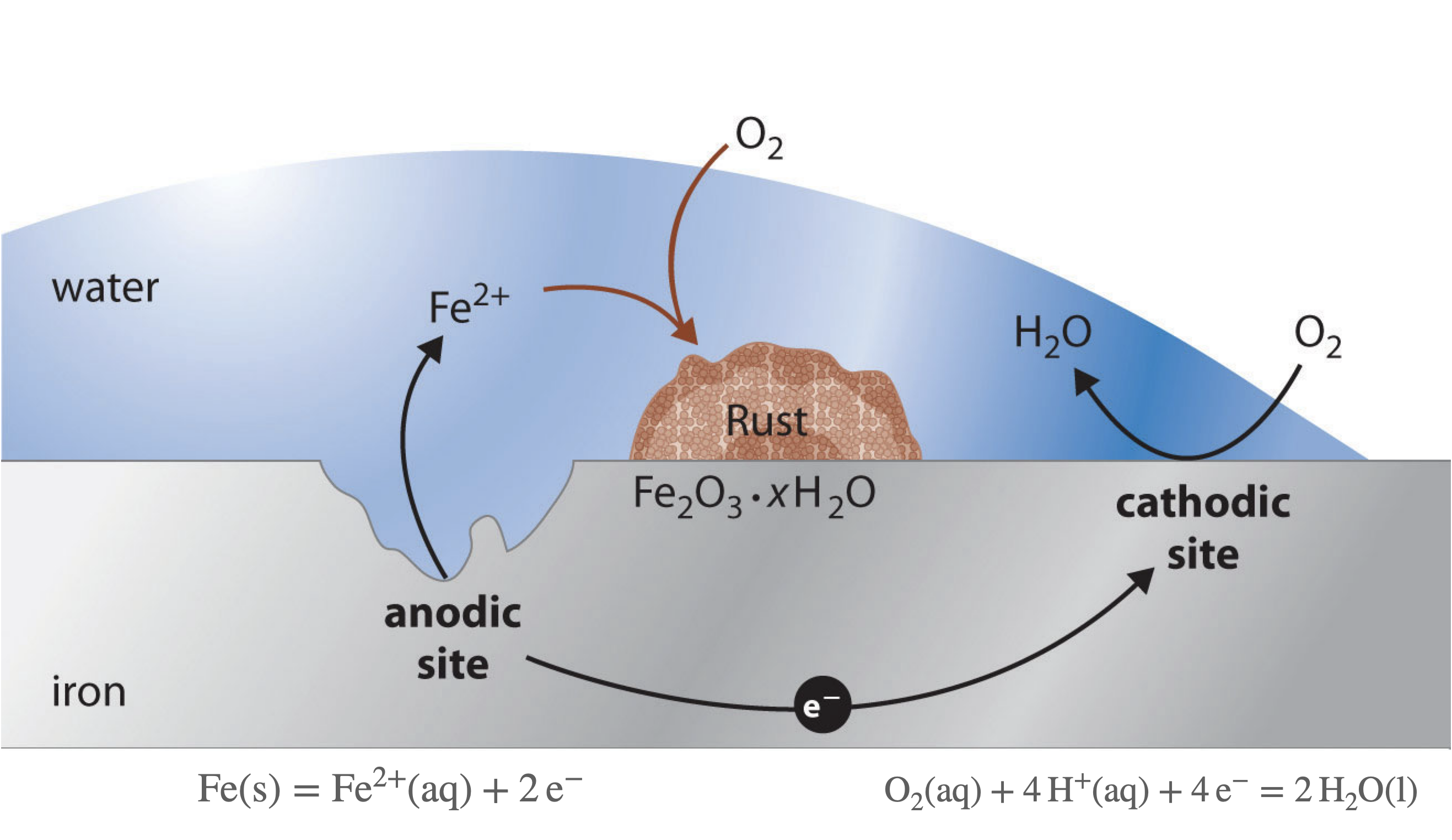
  • le dioxygène $\ce{O2 (g)}$ utilisé dans la respiration et les piles à combustible.

le dioxygène dissous $\ce{O2(aq)}$ est, lui,
responsable de la corrosion.


  • l'ion hypochlorite $\ce{CℓO^-}$ utilisé dans l'eau de Javel.
  • dichlore $\ce{Cℓ2}$ utilisé dans la production d'acide chlorhydrique.
  • dichlore $\ce{Cℓ2}$ utilisé dans la production d'acide chlorhydrique.

Parmi les réducteurs, on peut citer :

  • le dihydrogène $\ce{H2 (g)}$ utilisé dans les piles à hydrogène ou encore la production d'acide chlorhydrique ;
  • le glucose, réducteur dans la réaction de la respiration aérobie ;
  • l'acide ascorbique (vitamine C), antioxydant dans l'alimentation.

La présence d’un seul ou deux électrons de valence pour les métaux du bloc $\mathrm{s}$ du tableau périodique (lithium, sodium, magnésium, etc.) leur un caractère fortement réducteur (ils veulent ’en débarrasser).

C'est pour ça qu'ils se retrouvent au cœur de nombreuses piles (pile alcaline, pile lithium-ion,
pile magnésium-soufre, etc.).

La famille des alcalins est même capable
de réduire l'eau, ce qui peut provoquer
leur enflammement à son contact !

Principe de fonctionnement

Lorsqu’un oxydant est en contact d’un réducteur,
une transformation spontanée peut avoir lieu.

Cette réaction d'oxydo-réduction correspond à
un transfert d'électrons du reducteur vers l'oxydant.

Séparer les réactifs et les relier par un conducteur permet d’externaliser le transfert d’électrons.

C'est le principe d'une pile.

Une pile est en réalité constituée de deux demi-piles.

Chaque demi-pile abrite les deux membres
d'un couple oxydant-réducteur.

$\mathrm{(Ox_1/Red_1)}$ dans la demi-pile 1
et $\mathrm{(Ox_2/Red_2)}$ dans la demi-pile 2.

Et dans chaque demi-pile a lieu une des deux demi-équations électroniques.

Chaque demi-pile a besoin de
deux ingrédients supplémentaires :


  • une électrode faite d'un matériau
    conducteur solide qui va servir
    d'interface avec le circuit extérieur.

  • un électrolyte (milieu conducteur
    par déplacement d'ions).

Rq : l'électrode peut être directement l'oxydant ou le réducteur s'il est métallique ou un conducteur inerte comme du graphite ou du platine.

Supposons que la réaction spontanée
ait lieu entre $\mathrm{Ox_1}$ et $\mathrm{Red_2}$.


  • La demi-pile 2 est alors le siège de l'oxydation
    et va donc fournir les électrons. Son électrode, appelée anode est ainsi le pole négatif de la pile.

  • La demi-pile 1 est, elle, le siège de la réduction
    et va donc capter les électrons. Son électrode, appelée cathode est ainsi le pole positif de la pile.

⚠️

Les noms anodes et cathodes ne sont pas liés à la polarité (on verra que pour l’électrolyseur, les polarités sont inversées : l’anode est le pole $\oplus$ alors que
la cathode est le pole $\ominus$).

Mais les noms sont liés à la réaction :

  • la cathode est toujours le siège de la réduction.
  • L'anode est toujours le siège de l'oxydation.

Plus qu’à connecter les deux électrodes au circuit électrique qu’on cherche à alimenter.

Mais pour que du courant circule il faut assurer
un contact électrique entre les deux demi-piles
grâce à une jonction électrolytique
(pont salin, membrane, vase poreux, etc.).

Rôle du pont salin :

Maintien de la neutralité électrique
en fermant le circuit

Lorsque la réaction redox se produit, des électrons circulent dans le circuit externe, ce qui crée un déséquilibre de charges dans les solutions
des deux demi-piles.

Le pont salin permet alors le déplacement d’ions (anions vers l’anode et cations vers la cathode)
pour compenser ce déséquilibre.

Que se passerait-il sans le pont salin ?

Le déséquilibre de charge créerait un champ électrique qui finirait par stopper le flux d’électrons, phénomène que l’on appelle la polarisation des demi-piles.

L’intérêt du pont salin est d’assurer cette jonction électrolytique sans mélanger les deux solutions !

Sinon, on irait à l'encontre même du principe de la pile qui était de séparer l'oxydation et la réduction pour externaliser le transfert d'électrons.

Et pourtant…

Voici le schéma d’une pile très utilisée à la fin du 19e siècle (elle alimentait la plupart des télégraphes).

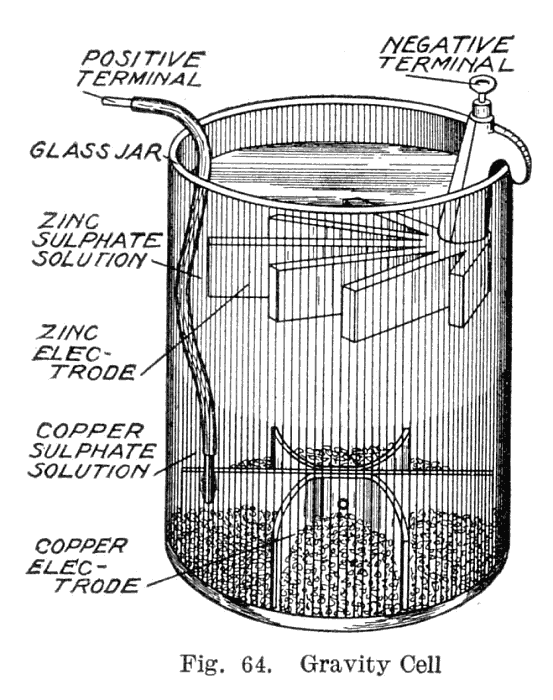
Comment ça marche ?


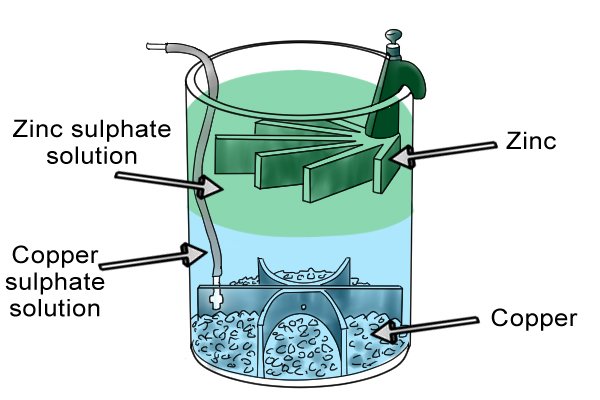
Donc il peut malgré tout y avoir un léger mélange des solutions (c’est aussi le cas avec un pont salin) mais du moment que les concentrations d’un même électrolyte restent très différents dans les deux compartiments,
la réaction est maintenue.

Déplacement des charges

Sur le schéma d’une pile, il faut savoir indiquer :

  • les polarités des électrodes ;
  • le déplacement des électrons
    dans le circuit électrique ;
  • le sens conventionnel du courant
    dans le circuit électrique ;
  • les déplacement des électrolytes
    dans le pont salin.

Le schéma suivant indique ces déplacements
dans le cas de la pile Daniell.

Étude quantitative

Tension à vide


La tension à vide d’une pile est la valeur absolue
de la tension mesurée entre ses électrodes
en circuit ouvert, c’est-à-dire quand aucun
courant électrique ne la traverse.

Cette tension à vide est mesurée en branchant
les électrodes aux bornes d'un voltmètre.

Rq : la tension à vide est aussi appelée force électromotrice (f.e.m.) de la pile.

Capacité électrique


La capacité électrique $Q$ d’une pile est la charge électrique maximale que la pile est susceptible
de faire circuler dans un circuit extérieur.

$ \begin{aligned} Q &=n(\text{é})_\mathrm{max}\times N_A\times e\\ &= n_\text{é}\times \mathcal{F} \end{aligned} $
  • $n(\text{é})_\mathrm{max}$ est la quantité maximale
    d'électrons échangés
    (en $\pu{mol}$)
  • $N_A$ est le nombre d'Avogadro
    ($N_A=\pu{6,02E23 mol-1}$)
  • $e$ est la charge élémentaire
    ($e=$$\pu{1,60E-19 C}$)
  • $\mathcal{F}$ est la constante de Faraday
    $\mathcal{F}=$$\color{#FFF056}{e\times N_A}$
    $\phantom{\mathcal{F}}=\pu{96,5E3 C*mol-1}$

Comment trouve-t-on $n(\text{é})_\mathrm{max}$ ?

  • On détermine le nombre $\nu_\text{é}$ d'électrons
    échangés dans l'équation globale de
    la réaction de fonctionnement de la pile.
  • Puis on détermine l'avancement maximal
    $x_\mathrm{max}$ de la réaction.

On a alors :

$n_\text{é} = \nu_\text{é}\times x_\mathrm{max}$

Exemple :

Une pile cuivre-aluminium repose sur
les deux couples oxydant/réducteur suivant :
$\ce{(Aℓ^3+(aq)/Aℓ(s))}$ et $\ce{(Cu^2+(aq)/Cu(s))}$

La transformation spontanée a lieu entre
les ions cuivre et l’aluminium.

  • Écrire l'équation de la réaction
    de fonctionnement de la pile
    à partir des demi-équations.
  • Combien d'électrons sont échangés
    dans cette réaction ?

Composition de la pile :

  • demi-pile 1 : électrode de 35 g d’aluminium
    dans 200 mL d’une solution de sulfate d’aluminium
    $\pu{0,50 mol*L-1}$ ;
  • demi-pile 2 : électrode de 50 g de cuivre dans 200 mL d’une solution de sulfate de cuivre à $\pu{0,50 mol*L-1}$ ;
  • Calculer l'avancement maximale
    de la réaction supposée totale.
  • En déduire la capacité électrique
    de la pile.

Durée de fonctionnement


L’intensité $I$ délivrée (supposée constante), la capacité électrique $Q$ et la durée de vie $\Delta t_\mathrm{max}$ de la pile
sont reliées par la relation :


$ \begin{aligned} Q = I\times\Delta t_\mathrm{max} \end{aligned} $

  • $Q$ en C
  • $I$ en A
  • $\Delta t_\mathrm{max}$ en s

Rq 1 :

Cette relation permet aussi de trouver la capacité électrique $Q$ si on nous donne l'intensité $I$ et la durée maximale de fonctionnement $\Delta t_\mathrm{max}$ !


Rq 2 :

Industriellement, la capacité est
le plus souvent donnée en $\pu{Ah}$ ou $\pu{mAh}$.
Conversion : 1 mAh $=$ 3,6 C

Retour site