Conduction thermique

Que nous apprend cette image ?

L’immeuble au premier plan est beaucoup mieux isolé que celui en arrière plan !

Cela se traduit par un plus faible flux thermique à travers sa paroi et ainsi un plus fort écart de température entre l'extérieur et l'intérieur.

Flux thermique

Le flux thermique à travers une paroi est l’énergie qui traverse cette paroi
par unité de temps.

Le flux est toujours orienté du chaud vers le froid.

Le flux thermique $\Phi$ à travers une paroi dépend

  • de la surface $S$ de la paroi,
  • de l'écart de température $\Delta \theta$
    de part et d'autre de la paroi,
  • et de la résistance thermique $R_{th}$ de la paroi.

Flus thermique $\Phi$ à travers la paroi (en W) :


$\displaystyle \Phi = \frac{S \Delta \theta}{R_{th}}=\frac{S\left(\theta_{\text{chaud}}-\theta_{\text{froid}}\right)}{R_{th}}$

  • $S$ en $\pu{m2}$
  • $\theta_{\text{chaud}}$ et $\theta_{\text{froid}}$ en °C ou K
  • $R_{th}$ en $\pu{K.m^2.W-1}$

En hiver, $\Phi$ donne l’énergie thermique perdue chaque seconde par une habitation.






Elle doit être compensée par un chauffage
de même puissance pour maintenir l’écart de température $\Delta \theta$ entre intérieur et extérieur.

À l’inverse, en été, le flux est souvent en journée
de l’extérieur vers l’intérieur.






Il donne la puissance d’un climatiseur devant maintenir une température intérieure
plus fraiche que l’extérieur.

Comment faire pour diminuer $\Phi$ ?


➘ $\Delta \theta$

ce qui revient à diminuer son confort thermique

➘ $S$

ce qui revient à avoir des petites ouvertures
et le moins de décrochements possible

➚ $R_{th}$

ce qui revient à améliorer l’isolation

Résistance thermique

La résistance thermique $R_{th}$
d’une paroi d’$\pu{1 m2}$ dépend :

  • de son épaisseur $e$ (en $\pu{m}$),
  • de la conductivité thermique $\lambda$ (en $\pu{W * m-1 * K-1}$) du matériau qui la constitue.

La conductivité thermique est une caractéristique intrinsèque d’un matériau traduisant sa capacité à diffuser l’énergie thermique à travers lui.

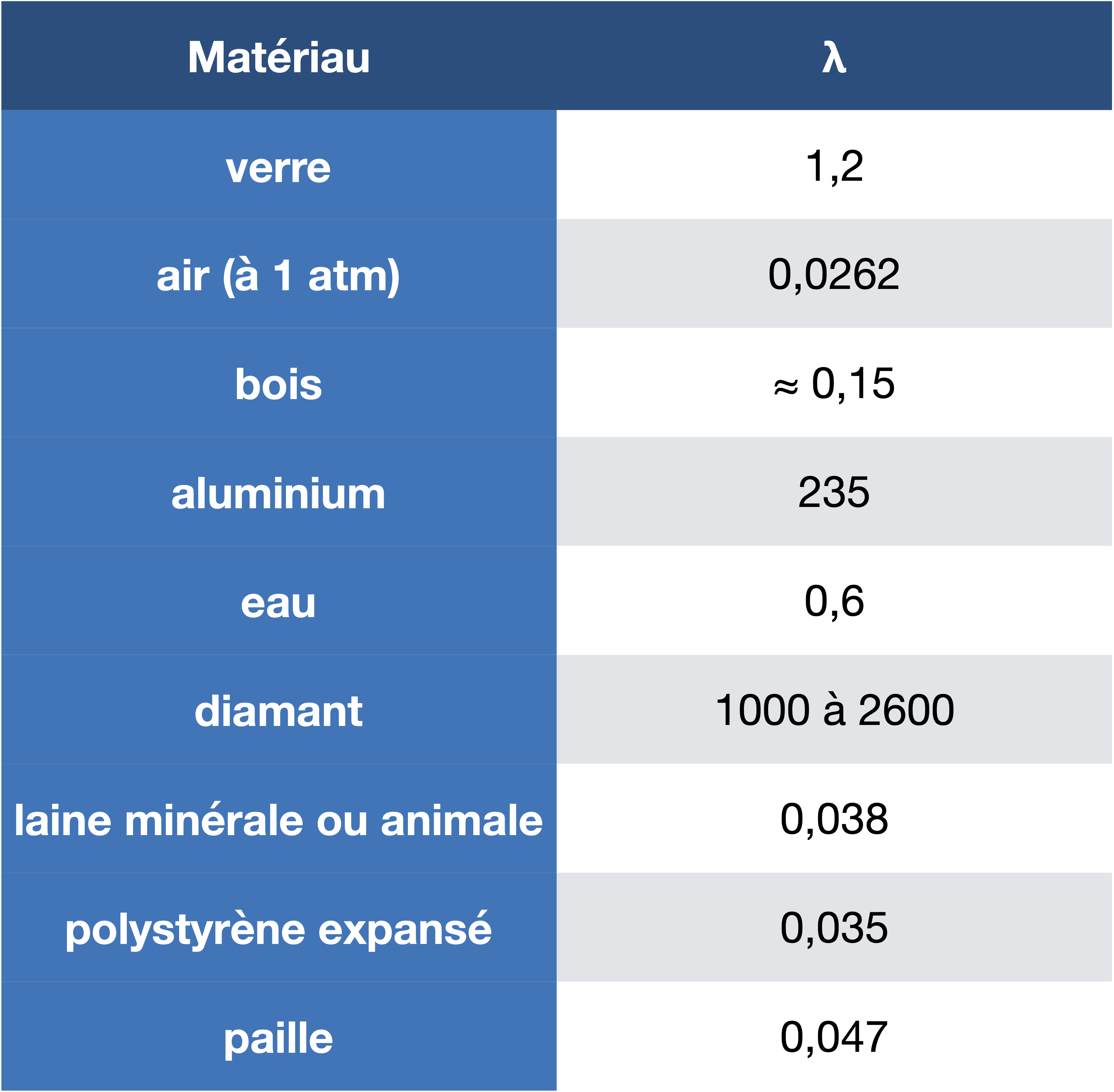
Expliquez le double vitrage
à l’aide du tableau précédent.

Comment construire la grandeur $R_{th}$
à partir de $e$ et $\lambda$.

Pour une paroi homogène :


$\displaystyle R_{th} = \frac{e}{\lambda}$

  • $R_{th}$ en $\pu{m2 * K * W-1}$
  • $e$ en $\pu{m}$.
  • $\lambda$ en $\pu{W*K-1*m-1}$

Les résistances thermiques
de parois superposées s’ajoutent.










Retour site