Exercice 1

• direction : horizontale
• sens : vers l’avant

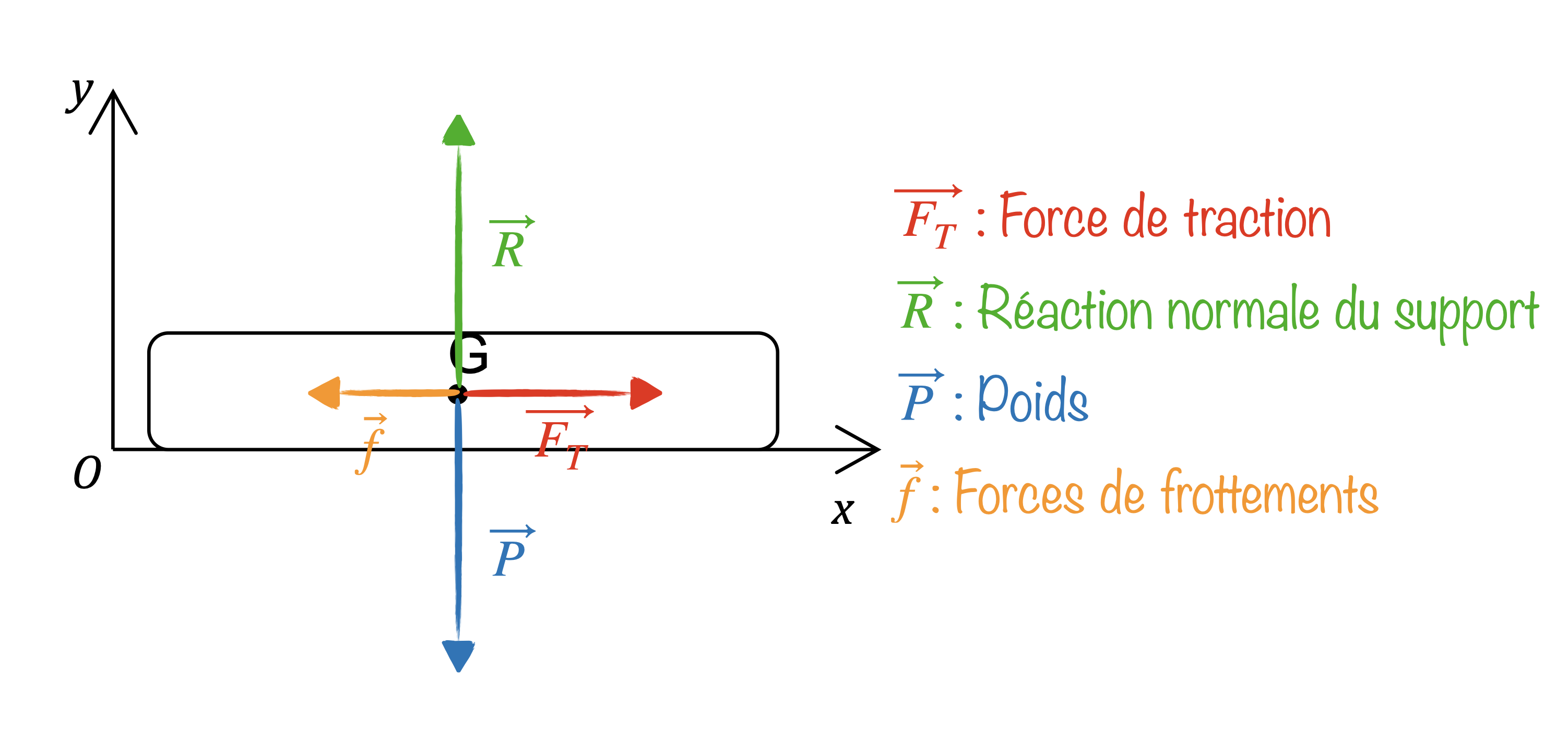
Principe fondamentale de la dynamique :

$m\vec{a} = \vec{f} + \vec{F_T} + \vec{P} + \vec{R}$

Comme le mouvement est horizontal, les forces verticales se compensent : $\vec{P}+\vec{R}=\vec{0}$

Et on néglige les frottement : $f\approx 0$

Conclusion : $m\vec{a} = \vec{F_T} \Rightarrow F_T=m\times a$

Prenons le cas où l’avion est le plus lourd
(au décollage) :

$ \begin{aligned} F_T &= m\times a\\ &= \pu{73500}\times 0,585 \\ &= \pu{42,8 kN} \end{aligned} $

Exercice 2

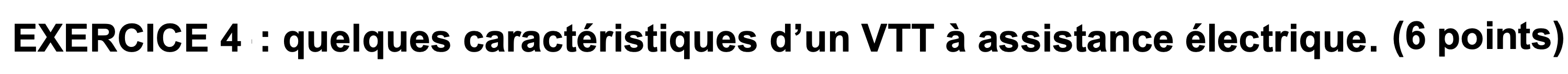
$ \begin{aligned} v &= \frac{d}{\Delta t}\\ & = \frac{\pu{7,54E3 m}}{\pu{30 min} \times \pu{60 s/min}}\\ &= \pu{4,2 m*s-1} \end{aligned} $

Le travail d’une force est égal au produit de la force par le déplacement dans la direction de cette force.

$W(\vec{P} )= \vec{P}\cdot\vec{AB}$

Donc dans le cas du poids :

$W(\vec{P} )= -mg\Delta z$

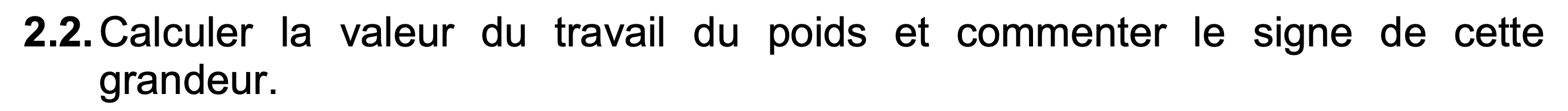
$ \begin{aligned} W(\vec{P} )&= -85\times9,8\times 5,8\cdot 10^2\\ &=\pu{-4,8E5 J} \end{aligned} $

Le travail du poids est négatif donc résistant.
Il agit en effet ici contre le mouvement
étant donné que le vététiste grimpe.

$P_{\text{apportée}} = 111 + 111\times160\% = \pu{289 W}$

$E_{\text{apportée}} = P_{\text{apportée}}\times \Delta t$

$ \begin{aligned} E_\text{air} &= P_\text{air}\times \Delta t\\ &= k \times v^3\times \Delta t \end{aligned} $

Le bilan d’énergie consiste à comparer
l’énergie apporté $E_\text{apportée}$ d’un côté
à l’énergie perdue $E_\text{perdue}$ de l’autre.

Du côté négatif, l'énergie est perdue
de deux façons :

• par les frottements,
• et surtout par le travail du poids.

$ \begin{aligned} E_\text{air} &= \pu{0,25 W*s^3*m-3}\times (\pu{4,2 m*s-1})^3\times \pu{1800 s}\\\\ &= \pu{3,3E4 J} \end{aligned} $

$ \begin{aligned} E_\text{perdue} &= E_\text{air} + |W(\vec{P})|\\\\ &= \pu{3,3E4 J}+ \pu{4,8E5 J}\\\\ &= \pu{5,1E5 J} \end{aligned} $

Finalement $E_\text{apportée}$ $>$ $E_\text{perdue}$ , le vététiste peut donc parvenir à son but (il a assez d’énergie pour).

On a négligé la résistance au roulement dans ce traitement, on peut supposer qu’en les prenant en compte, le temps nécessaire augmente de 5 min.