Qu’est-ce qu’une mole ?
Un paquet de 602 mille milliards de milliardsBut de cette définition ?
Une mole de nucléons pèse 1 g !
On déduit la masse molaire M du nombre de nucléons du noyau de l’atome :
Hydrogène
très majoritairement composé de l’isotope $^{1}_{1}\text{H}$
M = 1 g.mol-1
Carbone
très majoritairement composé de l’isotope $^{12}_{\hphantom{0}6}\text{C}$
M = 12 g.mol-1
Oxygène
très majoritairement composé de l’isotope $^{16}_{\hphantom{0}8}\text{O}$
M = 16 g.mol-1
On connaît la masse $m$ (en g), comment obtenir
la quantité de matière $n$ (en mol) ?
Volume ↔︎ Masse
Cas de l’eau :
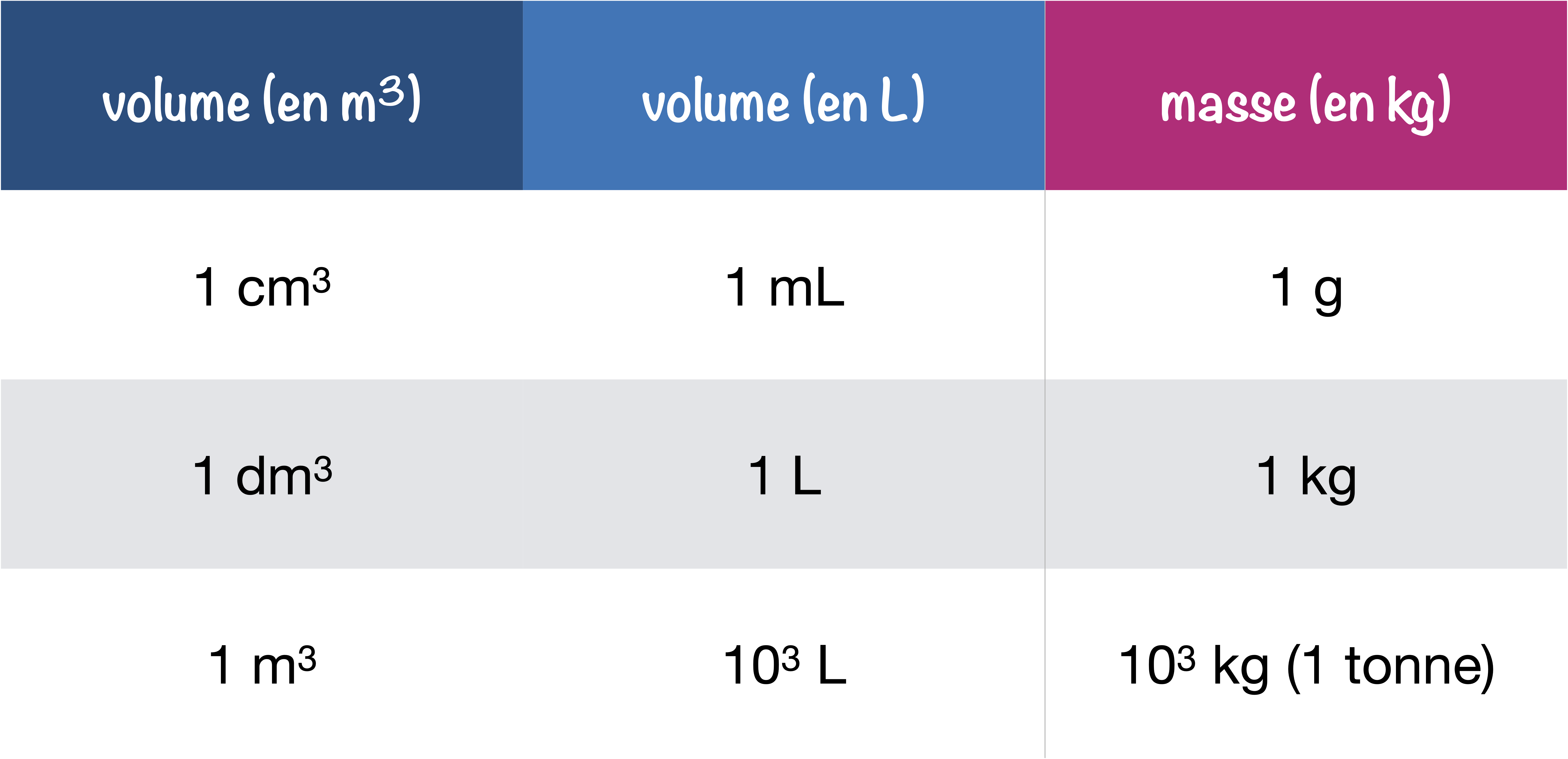
Pour autre chose que l’eau,
on utilise la masse volumique $\rho$ :
$$m=\rho\times V$$
Combien de moles d'eau dans un verre d'eau ?
$\approx$ 10 mol

Même solvant, même soluté, même volume… Qu’est-ce qui change entre ces 4 solutions ?
Concentration
massique
$$\color{#CB4335}\boxed{C_m=\frac{m}{V}}$$
m : masse du soluté (en g)
V : volume du solvant (en L)
unité : g.L-1
molaire
$$\color{#CB4335}\boxed{C=\frac{n}{V}}$$
n : quantité de matière du soluté (en mol)
V : volume du solvant (en L)
unité : mol.L-1
parfois notée [X] où X est le symbole chimique de l’espèce
(surtout pour les ions)
Comment fabrique-t-on une solution d’une concentration massique ou molaire donnée ?
Par dissolution !Dissolution d’un soluté dans un solvant
Protocole :
On connaît le volume $V$ (en L) d’une solution, comment obtenir la quantité de matière (en $\pu{mol}$) d’un soluté de concentration $C$ (en $\pu{mol * L-1}$) ?
$$n =C\times V$$
Une solution est trop concentrée.
Que peut-on faire ?
Dilution
Matériel utilisé ?
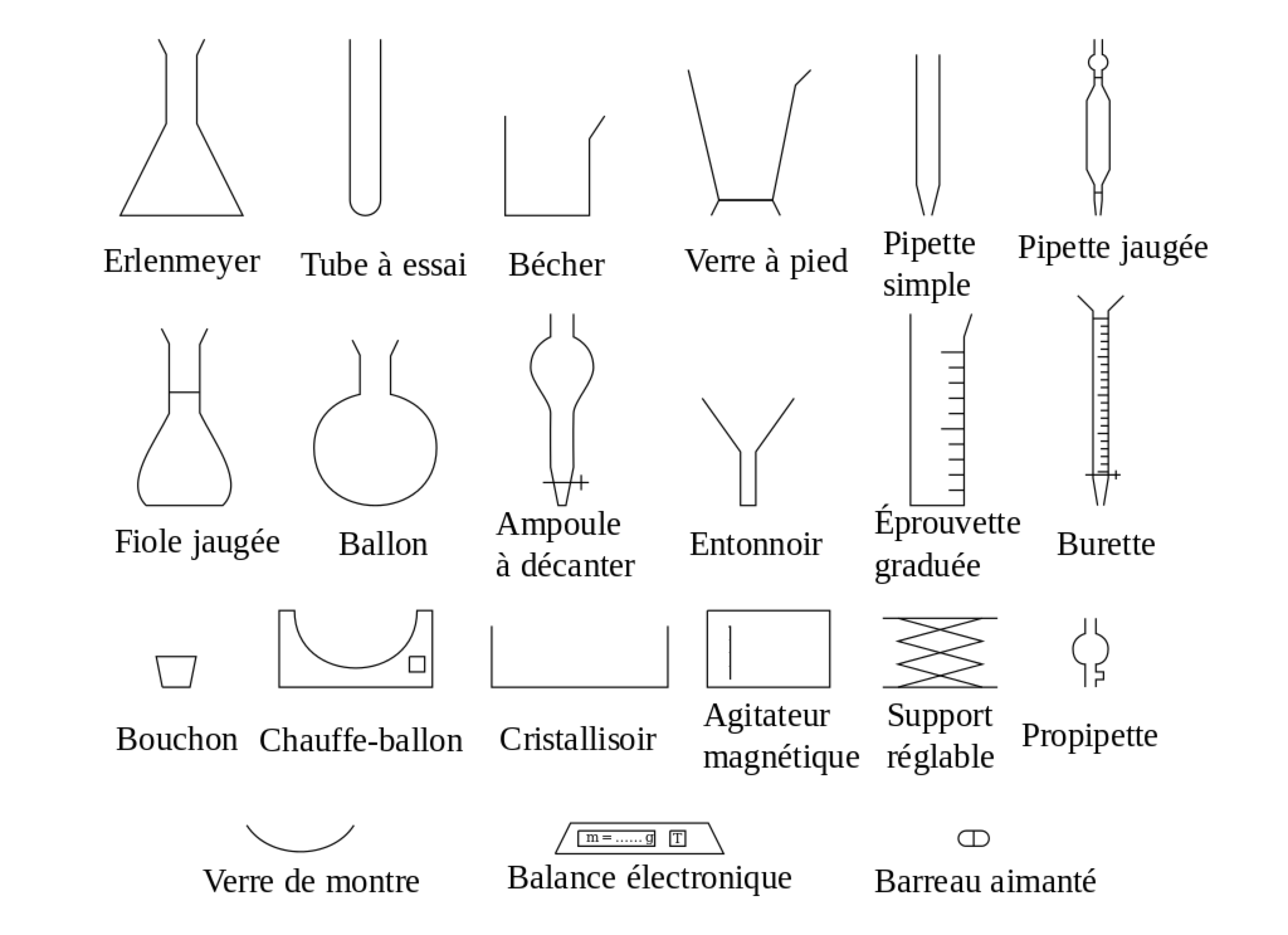
Matériel utilisé ?

Protocole :
Soit $X$ le facteur de dilution (on veut diluer $X$ fois).
Quel est le lien entre $X$, Cfille et Cmère ?
$$X = \frac{\text{C}_\text{mère}}{\text{C}_\text{fille}}$$
Entre $X$, Vfille et Vmère ?
$$X = \frac{\text{V}_\text{fille}}{\text{V}_\text{mère}}$$
Entre $X$, Vpipette et Vfiole ?
$$X = \frac{\text{V}_\text{fiole}}{\text{V}_\text{pipette}}$$